



Next: De golfvergelijking
Up: Fourieranalyse van golfverschijnselen
Previous: Fouriertransformatie
Contents
Beschrijving van een golfpakket
Als voorbeeld beschouwen we een golf die op 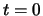 beschreven wordt
door de functie
beschreven wordt
door de functie 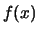 afgebeeld in Fig. 9. De golf
wordt `gechopped', waardoor er een puls of golfpakket
met lengte
afgebeeld in Fig. 9. De golf
wordt `gechopped', waardoor er een puls of golfpakket
met lengte
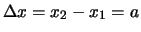 wordt verkregen. We stellen de golffunctie van de puls voor als
wordt verkregen. We stellen de golffunctie van de puls voor als
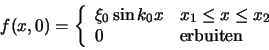 |
(56) |
Figuur 9:
Fourier analyse van een golfpakket met lengte 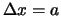 en amplitude
en amplitude
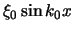 voor het interval
voor het interval
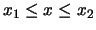 .
Links wordt het golfpakket gegeven, terwijl rechts het impulsspectrum
getoond wordt.
.
Links wordt het golfpakket gegeven, terwijl rechts het impulsspectrum
getoond wordt.
|
|
Elke functie kan geschreven worden als een superpositie van harmonische
golven. We schrijven dan
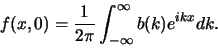 |
(57) |
Vervolgens proberen we de coëfficiënten te berekenen door
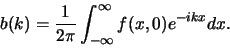 |
(58) |
We merken op dat de golffunctie
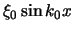 van de puls geschreven kan
worden als het imaginaire deel van
van de puls geschreven kan
worden als het imaginaire deel van 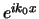 en vinden voor ons geval
en vinden voor ons geval
![\begin{displaymath}
b(k) = {1 \over \sqrt{2\pi a}} \int_{-a/2}^{+a/2} e^{ik_0x}...
...
= \sqrt{2 \over \pi a} {\sin{[(k-k_0)a/2]} \over k - k_0} .
\end{displaymath}](img301.png) |
(59) |
Deze amplitude is geschetst in het rechter paneel van Fig. 9.
Indien de originele puls,
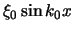 , zich uitstrekte van
, zich uitstrekte van
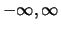 , dan was het niet nodig geweest om een Fourieranalyse
te maken, omdat de kromme dan een harmonische beweging met golfgetal
, dan was het niet nodig geweest om een Fourieranalyse
te maken, omdat de kromme dan een harmonische beweging met golfgetal
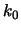 voorstelde. Echter, om de kromme voor
voorstelde. Echter, om de kromme voor 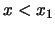 en
en 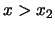 tot nul te reduceren moeten we andere frequenties toevoegen, zodat
de resulterende Fourierreeks in die gebieden nul is. Een eindige
puls is dus een samenstelling van vele frequenties, ook al heeft
de trillingsbron een zeer bepaalde frequentie.
tot nul te reduceren moeten we andere frequenties toevoegen, zodat
de resulterende Fourierreeks in die gebieden nul is. Een eindige
puls is dus een samenstelling van vele frequenties, ook al heeft
de trillingsbron een zeer bepaalde frequentie.
We zien dat het frequentiespectrum 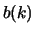 een maximum heeft voor
een maximum heeft voor 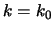 .
Het gebied van
.
Het gebied van 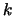 waarvoor
waarvoor 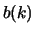 groter is dan de helft van het maximum
voldoet bij benadering aan de voorwaarde
groter is dan de helft van het maximum
voldoet bij benadering aan de voorwaarde
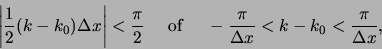 |
(60) |
waarbij 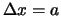 . Als we dus stellen dat
. Als we dus stellen dat
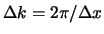 ,
dan zien we dat de enige frequenties met behoorlijke amplitudes in het
gebied
,
dan zien we dat de enige frequenties met behoorlijke amplitudes in het
gebied 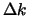 rond het maximum
rond het maximum 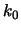 liggen, gegeven door
liggen, gegeven door
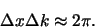 |
(61) |
We zien dat hoe korter de tijdsduur van de puls is, des te groter
het frequentiegebied is dat nodig is om de puls nauwkeurig voor
te stellen.




Next: De golfvergelijking
Up: Fourieranalyse van golfverschijnselen
Previous: Fouriertransformatie
Contents
Jo van den Brand
2004-09-25
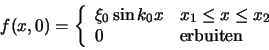
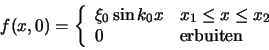
![\includegraphics[width=14cm]{Figures/sinx.eps}](img296.png)
![\begin{displaymath}
b(k) = {1 \over \sqrt{2\pi a}} \int_{-a/2}^{+a/2} e^{ik_0x}...
...
= \sqrt{2 \over \pi a} {\sin{[(k-k_0)a/2]} \over k - k_0} .
\end{displaymath}](img301.png)
![]() , zich uitstrekte van
, zich uitstrekte van
![]() , dan was het niet nodig geweest om een Fourieranalyse
te maken, omdat de kromme dan een harmonische beweging met golfgetal
, dan was het niet nodig geweest om een Fourieranalyse
te maken, omdat de kromme dan een harmonische beweging met golfgetal
![]() voorstelde. Echter, om de kromme voor
voorstelde. Echter, om de kromme voor ![]() en
en ![]() tot nul te reduceren moeten we andere frequenties toevoegen, zodat
de resulterende Fourierreeks in die gebieden nul is. Een eindige
puls is dus een samenstelling van vele frequenties, ook al heeft
de trillingsbron een zeer bepaalde frequentie.
tot nul te reduceren moeten we andere frequenties toevoegen, zodat
de resulterende Fourierreeks in die gebieden nul is. Een eindige
puls is dus een samenstelling van vele frequenties, ook al heeft
de trillingsbron een zeer bepaalde frequentie.
![]() een maximum heeft voor
een maximum heeft voor ![]() .
Het gebied van
.
Het gebied van ![]() waarvoor
waarvoor ![]() groter is dan de helft van het maximum
voldoet bij benadering aan de voorwaarde
groter is dan de helft van het maximum
voldoet bij benadering aan de voorwaarde