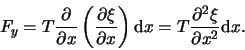Next: Partiële afgeleiden en oplossingen
Up: KLASSIEKE GOLFVERSCHIJNSELEN
Previous: Beschrijving van een golfpakket
Contents
In het volgende gaan we na hoe we kunnen bepalen of een bepaald
fysisch verschijnsel, voorgesteld door een gegeven tijdafhankelijk
veld, zich als een golf zonder vervorming voortplant. De
velden worden veelal door dynamische wetten beheerst, die in de
vorm van differentiaalvergelijkingen kunnen worden uitgedrukt.
De vergelijking die het golfverschijnsel beschrijft wordt de
golfvergelijking genoemd en dit is in het algemeen een
differentiaalvergelijking. Als voorbeeld bespreken we hier de
transversale golven op een snaar (van bijvoorbeeld een gitaar).
Figuur 10:
Een snaar waarin een spankracht 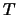 heerst wordt over
een kleine afstand
heerst wordt over
een kleine afstand 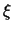 vanuit zijn evenwichtstoestand verplaatst.
We beschouwen een deel AB met lengte d
vanuit zijn evenwichtstoestand verplaatst.
We beschouwen een deel AB met lengte d .
.
|
|
In de snaar heerst een spankracht 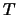 en in de evenwichtstoestand
is de snaar recht. Vervolgens verplaatsen we de snaar loodrecht op
zijn lengterichting over een kleine afstand (zie Fig. 20).
We beschouwen een deel AB met lengte d
en in de evenwichtstoestand
is de snaar recht. Vervolgens verplaatsen we de snaar loodrecht op
zijn lengterichting over een kleine afstand (zie Fig. 20).
We beschouwen een deel AB met lengte d dat zich op een afstand
dat zich op een afstand
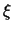 van de evenwichtstoestand bevindt. Omdat we de verplaatsing
van de evenwichtstoestand bevindt. Omdat we de verplaatsing
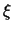 klein aannemen, mogen we aannemen dat de tangentiële spankracht
in elk punt van de snaar gelijk is gebleven. Wegens de kromming van
de snaar zijn de krachten
klein aannemen, mogen we aannemen dat de tangentiële spankracht
in elk punt van de snaar gelijk is gebleven. Wegens de kromming van
de snaar zijn de krachten 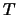 niet precies tegengesteld gericht. De
resulterende kracht op het stuk AB in naar boven gericht en bedraagt
niet precies tegengesteld gericht. De
resulterende kracht op het stuk AB in naar boven gericht en bedraagt
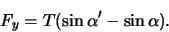 |
(62) |
Omdat de snaar slechts zwak gekromd is, zijn de hoeken 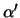 en
en 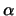 klein en kunnen ze door hun tangenten vervangen worden.
We vinden
klein en kunnen ze door hun tangenten vervangen worden.
We vinden
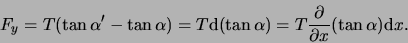 |
(63) |
We merken op dat 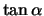 de helling van de snaar is en deze
is gelijk aan
de helling van de snaar is en deze
is gelijk aan
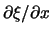 . We vinden hiermee
. We vinden hiermee
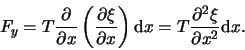 |
(64) |
De massa per lengte-eenheid van de snaar is 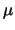 en de massa van het
stuk AB is gelijk aan
en de massa van het
stuk AB is gelijk aan 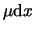 . We gebruiken nu de tweede wet
van Newton,
. We gebruiken nu de tweede wet
van Newton,
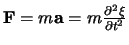 ,
die de dynamica beschrijft en vinden
,
die de dynamica beschrijft en vinden
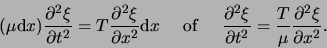 |
(65) |
Dit is de golfvergelijking die transversale trillingen op een
snaar beschrijft als de amplitude klein is. De voortplantingssnelheid
van de transversale golf is
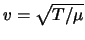 .
.
Subsections




Next: Partiële afgeleiden en oplossingen
Up: KLASSIEKE GOLFVERSCHIJNSELEN
Previous: Beschrijving van een golfpakket
Contents
Jo van den Brand
2004-09-25
![\includegraphics[width=14cm]{Figures/snaar.eps}](img312.png)
![\includegraphics[width=14cm]{Figures/snaar.eps}](img312.png)
![]() en in de evenwichtstoestand
is de snaar recht. Vervolgens verplaatsen we de snaar loodrecht op
zijn lengterichting over een kleine afstand (zie Fig. 20).
We beschouwen een deel AB met lengte d
en in de evenwichtstoestand
is de snaar recht. Vervolgens verplaatsen we de snaar loodrecht op
zijn lengterichting over een kleine afstand (zie Fig. 20).
We beschouwen een deel AB met lengte d![]() dat zich op een afstand
dat zich op een afstand
![]() van de evenwichtstoestand bevindt. Omdat we de verplaatsing
van de evenwichtstoestand bevindt. Omdat we de verplaatsing
![]() klein aannemen, mogen we aannemen dat de tangentiële spankracht
in elk punt van de snaar gelijk is gebleven. Wegens de kromming van
de snaar zijn de krachten
klein aannemen, mogen we aannemen dat de tangentiële spankracht
in elk punt van de snaar gelijk is gebleven. Wegens de kromming van
de snaar zijn de krachten ![]() niet precies tegengesteld gericht. De
resulterende kracht op het stuk AB in naar boven gericht en bedraagt
niet precies tegengesteld gericht. De
resulterende kracht op het stuk AB in naar boven gericht en bedraagt