



Next: Een opgesloten deeltje
Up: GOLFKARAKTER VAN MATERIE
Previous: Het golfkarakter van materie
Contents
Als we licht als een golfverschijnsel interpreteren en spreken
over bijvoorbeeld de golflengte, dan hebben we in gedachten dat
licht een configuratie van elektrische en magnetische velden is
die zich met de lichtsnelheid voortplant in de ruimte.
Materiegolven worden beschreven door een golffunctie 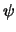 .
Dergelijke golven beschrijven de beweging van deeltjes op dezelfde manier
als elektromagnetische golven de beweging van fotonen beschrijven.
We weten echter niet welke grootheid in geval van een materiegolf
correspondeert met bijvoorbeeld
het elektrische veld van een elektromagnetische golf.
We beschouwen allereerst een nuttig theorema dat van toepassing is
op alle soorten golven. Als we denken aan golven op een snaar, dan
weten we dat we een lopende golf van elke willekeurige
golflengte zich kan voorplanten langs een snaar met oneindige
lengte. Echter op een gespannen snaar van eindige lengte
kunnen slechts staande golven bestaan en deze hebben een
discrete set van golflengten. We kunnen onze ervaring
samenvatten door te stellen dat: lokalisatie van een golf in de
ruimte tot gevolg heeft dat slechts een discrete set golflengten,
en hiermee dus een discrete set frequenties, kan voorkomen.
Kortom: lokalisatie leidt tot quantisatie. Dit theorema geldt niet
alleen voor golven op een snaar, maar voor alle soorten golven,
inclusief elektromagnetische golven en zoals we in het vervolg
zullen zien, materiegolven.
.
Dergelijke golven beschrijven de beweging van deeltjes op dezelfde manier
als elektromagnetische golven de beweging van fotonen beschrijven.
We weten echter niet welke grootheid in geval van een materiegolf
correspondeert met bijvoorbeeld
het elektrische veld van een elektromagnetische golf.
We beschouwen allereerst een nuttig theorema dat van toepassing is
op alle soorten golven. Als we denken aan golven op een snaar, dan
weten we dat we een lopende golf van elke willekeurige
golflengte zich kan voorplanten langs een snaar met oneindige
lengte. Echter op een gespannen snaar van eindige lengte
kunnen slechts staande golven bestaan en deze hebben een
discrete set van golflengten. We kunnen onze ervaring
samenvatten door te stellen dat: lokalisatie van een golf in de
ruimte tot gevolg heeft dat slechts een discrete set golflengten,
en hiermee dus een discrete set frequenties, kan voorkomen.
Kortom: lokalisatie leidt tot quantisatie. Dit theorema geldt niet
alleen voor golven op een snaar, maar voor alle soorten golven,
inclusief elektromagnetische golven en zoals we in het vervolg
zullen zien, materiegolven.
Figuur 20:
Vier patronen voor staande golven op een snaar met
lengte 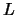 . Het patroon voor
. Het patroon voor 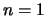 komt overeen met de grootst
mogelijke golflengte (en de laagste frequentie) waarmee de golf
kan oscilleren.
komt overeen met de grootst
mogelijke golflengte (en de laagste frequentie) waarmee de golf
kan oscilleren.
|
|
Fig. 20 toont enkele van de staande golven die kunnen
bestaan op een snaar met lengte 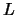 .
We kunnen deze patronen zien als stationaire
toestanden van de trillende snaar, die optreden bij frequenties
die gequantiseerd zijn volgens de relatie
.
We kunnen deze patronen zien als stationaire
toestanden van de trillende snaar, die optreden bij frequenties
die gequantiseerd zijn volgens de relatie
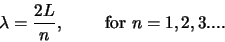 |
(112) |
Hierbij is 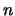 een integer die de modus van trilling bepaalt.
We zullen dergelijke integers quantumgetallen noemen.
De frequenties die corresponderen met deze golflengten zijn ook
gequantiseerd en we vinden
een integer die de modus van trilling bepaalt.
We zullen dergelijke integers quantumgetallen noemen.
De frequenties die corresponderen met deze golflengten zijn ook
gequantiseerd en we vinden
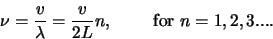 |
(113) |
Hierbij is 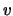 de golfsnelheid.
de golfsnelheid.




Next: Een opgesloten deeltje
Up: GOLFKARAKTER VAN MATERIE
Previous: Het golfkarakter van materie
Contents
Jo van den Brand
2004-09-25
![\includegraphics[width=7cm]{Figures/Fig7.eps}](img430.png)
![\includegraphics[width=7cm]{Figures/Fig7.eps}](img430.png)