Next: Waarschijnlijkheid
Up: GOLFKARAKTER VAN MATERIE
Previous: De golffunctie
Contents
Een opgesloten deeltje
Stel dat we straling opsluiten tussen twee perfect reflecterende
spiegels die een afstand 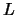 uit elkaar staan. We beperken
de discussie tot de modus met de grootste
golflengte (
uit elkaar staan. We beperken
de discussie tot de modus met de grootste
golflengte (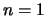 ). Licht is een elektromagnetische golf en
als we de amplitude van het elektrische veld (een vectorgrootheid)
). Licht is een elektromagnetische golf en
als we de amplitude van het elektrische veld (een vectorgrootheid)
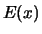 van deze golf zouden uitrekenen, dan vinden we hiervoor
van deze golf zouden uitrekenen, dan vinden we hiervoor
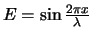 . Het elektrische veld verdwijnt voor
. Het elektrische veld verdwijnt voor
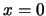 en
en 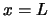 en heeft een maximum voor
en heeft een maximum voor 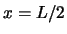 . De
energiedichtheid wordt gegeven door
. De
energiedichtheid wordt gegeven door
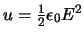 en we kunnen ons voorstellen dat de energiedichtheid op elk punt
veroorzaakt wordt door de dichtheid van fotonen op dat punt, waarbij
elk foton een energie
en we kunnen ons voorstellen dat de energiedichtheid op elk punt
veroorzaakt wordt door de dichtheid van fotonen op dat punt, waarbij
elk foton een energie 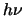 draagt. We concluderen hiermee dat het
kwadraat van de amplitude op elk punt van een staande elektromagnetische
golf evenredig is met de dichtheid van fotonen op dat punt.
We kunnen ook stellen dat de waarschijnlijkheid om een foton op een
bepaalde positie aan te treffen evenredig is met het kwadraat van de
amplitude die de elektromagnetische golf heeft op dat punt.
Merk op dat met deze formulering onze kennis van de fotonpositie
inherent statistisch bepaald is. We weten niet precies waar een
foton met een bepaalde impuls zich bevindt. Deze statistische
limitatie is fundamenteel zowel voor licht als materie.
draagt. We concluderen hiermee dat het
kwadraat van de amplitude op elk punt van een staande elektromagnetische
golf evenredig is met de dichtheid van fotonen op dat punt.
We kunnen ook stellen dat de waarschijnlijkheid om een foton op een
bepaalde positie aan te treffen evenredig is met het kwadraat van de
amplitude die de elektromagnetische golf heeft op dat punt.
Merk op dat met deze formulering onze kennis van de fotonpositie
inherent statistisch bepaald is. We weten niet precies waar een
foton met een bepaalde impuls zich bevindt. Deze statistische
limitatie is fundamenteel zowel voor licht als materie.
Figuur 21:
De waarschijnlijkheidsdichtheid voor vier toestanden van
een elektron dat is opgesloten in een oneindig diepe put. De
quantumgetallen zijn aangegeven.
|
|
Een eenvoudige inleiding tot materiegolven is de studie van de beweging
van een deeltje dat opgesloten is tussen vaste wanden. Met name
atomen zijn systemen, waarin elektronen zijn opgesloten.
Hier beschouwen we allereerst een ééndimensionaal probleem.
We kunnen de relevante golffunctie
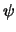 bestuderen dankzij de wiskundige relatie met twee klassieke
problemen: de staande-golf oscillaties van een korte, gespannen snaar
en de elektromagnetische oscillaties binnen een trilholte met ideaal
reflecterende wanden.
Met name de waarschijnlijkheid om een elektron op een bepaalde positie
aan te treffen (dit noemt men de waarschijnlijkheidsdichtheid)
is evenredig het het quadraat van de golffunctie op die positie.
In het ééndimensionale geval is
bestuderen dankzij de wiskundige relatie met twee klassieke
problemen: de staande-golf oscillaties van een korte, gespannen snaar
en de elektromagnetische oscillaties binnen een trilholte met ideaal
reflecterende wanden.
Met name de waarschijnlijkheid om een elektron op een bepaalde positie
aan te treffen (dit noemt men de waarschijnlijkheidsdichtheid)
is evenredig het het quadraat van de golffunctie op die positie.
In het ééndimensionale geval is
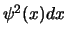 evenredig met de waarschijnlijkheid het deeltje aan te
treffen in het interval tussen
evenredig met de waarschijnlijkheid het deeltje aan te
treffen in het interval tussen  en
en 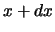 . Verder geldt dat
. Verder geldt dat
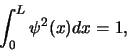 |
(114) |
waarmee de waarschijnlijkheid het deeltje ergens in het interval
tussen 0 en 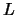 aan te treffen gelijk is aan 100 %.
Fig. 21 geeft de waarschijnlijkheidsdichtheid voor vier
toestanden van een elektron dat is opgesloten in een oneindig diepe
potentiaalput. De
energieën van het opgesloten elektron zijn gelimiteerd tot discrete
waarden, die als volgt gevonden kunnen worden. De potentiële
energie van het elektron in de put is gelijk aan nul en
de totale energie wordt dus gegeven door de kinetische energie
(
aan te treffen gelijk is aan 100 %.
Fig. 21 geeft de waarschijnlijkheidsdichtheid voor vier
toestanden van een elektron dat is opgesloten in een oneindig diepe
potentiaalput. De
energieën van het opgesloten elektron zijn gelimiteerd tot discrete
waarden, die als volgt gevonden kunnen worden. De potentiële
energie van het elektron in de put is gelijk aan nul en
de totale energie wordt dus gegeven door de kinetische energie
(
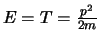 ). De impuls van het elektron wordt gegeven
door
). De impuls van het elektron wordt gegeven
door
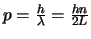 . We vinden dan voor
de totale energie
. We vinden dan voor
de totale energie
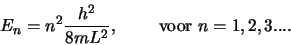 |
(115) |
De toestand met 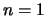 heeft de laagste energie en wordt
de grondtoestand genoemd. We merken op dat, in tegenstelling
tot de klassieke verwachtingen, het elektron niet in rust kan zijn
in de put. De reden is dat de laagste energie gegeven wordt
door
heeft de laagste energie en wordt
de grondtoestand genoemd. We merken op dat, in tegenstelling
tot de klassieke verwachtingen, het elektron niet in rust kan zijn
in de put. De reden is dat de laagste energie gegeven wordt
door
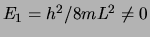 , en dat wordt ook wel de nulpuntsenergie
genoemd. Het is de energie van het deeltje bij een temperatuur
, en dat wordt ook wel de nulpuntsenergie
genoemd. Het is de energie van het deeltje bij een temperatuur  K.
K.




Next: Waarschijnlijkheid
Up: GOLFKARAKTER VAN MATERIE
Previous: De golffunctie
Contents
Jo van den Brand
2004-09-25
![\includegraphics[width=7cm]{Figures/Fig8.eps}](img439.png)
![\includegraphics[width=7cm]{Figures/Fig8.eps}](img439.png)