



Next: De golffunctie
Up: GOLFKARAKTER VAN MATERIE
Previous: GOLFKARAKTER VAN MATERIE
Contents
Het gebuik van symmetrieën is in de fysica buitengewoon nuttig
gebleken. Bijvoorbeeld toen we leerden dat een veranderend
magnetisch veld een elektrisch veld produceert, zoals dat bijvoorbeeld
met een fietsdynamo gebeurt, hadden we
kunnen verwachten - en dat blijkt ook zo te zijn - dat een
veranderend elektrisch veld een magnetisch veld produceert.
In 1924 reflecteerde Louis de Broglie over het feit dat licht
een dualistisch golf-deeltjes aspect heeft, terwijl materie
enkel deeljesachtig leek te zijn. Dit alles is moeilijk te rijmen als we
weten dat zowel licht als materie vormen van energie zijn, die
in elkaar over kunnen gaan. Hij concludeerde dan ook dat materie een
dergelijk dualistisch karakter dient te hebben en dat deeltjes zoals
elektronen golfachtig karakter vertonen.
De Broglie maakte de suggestie dat de relatie 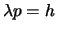 op zowel licht als materie van toepassing is.
Elektronenbundels en andere vormen van materie kunnen golfgedrag
vertonen, zoals interferentie en diffractie, met een
de Broglie golflengte gegeven door
op zowel licht als materie van toepassing is.
Elektronenbundels en andere vormen van materie kunnen golfgedrag
vertonen, zoals interferentie en diffractie, met een
de Broglie golflengte gegeven door
 |
(110) |
Deze golfeigenschappen kunnen het meest eenvoudig gedemonstreerd worden
met diffractie, analoog aan 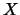 -ray diffractie, die optreedt tijdens
reflectie aan atoomvlakken in kristallen.
-ray diffractie, die optreedt tijdens
reflectie aan atoomvlakken in kristallen.
Figuur 18:
Elektronenbundels en andere vormen van materie kunnen golfgedrag
vertonen, zoals interferentie en diffractie.
|
|
Dit wordt schematisch
weergegeven in figuur 18. Hier geldt de
wet van Bragg,
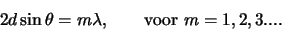 |
(111) |
waarbij 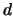 de roosterconstante van het kristal is en
de roosterconstante van het kristal is en
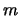 de orde van het intensiteitsmaximum.
de orde van het intensiteitsmaximum.
Figuur 19:
De linkerfiguur toont het diffractiepatroon voor de
verstrooiing van 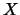 -rays aan een poeder van aluminium. De rechterfiguur
toont diffractie van een elektronenbundel met een energie van 15 eV.
-rays aan een poeder van aluminium. De rechterfiguur
toont diffractie van een elektronenbundel met een energie van 15 eV.
|
|
Fig. 19
toont diffractiepatronen die verkregen worden door 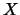 -rays of
elektronen te verstrooien aan aluminiumpoeder. Men kan concluderen
dat de gevonden patronen er geen twijfel over laten bestaan dat beide volgens
hetzelfde fysicamechanisme gegenereerd worden. Meting en analyse van dergelijke
patronen bevestigen de hypothese van de Broglie in elk detail.
-rays of
elektronen te verstrooien aan aluminiumpoeder. Men kan concluderen
dat de gevonden patronen er geen twijfel over laten bestaan dat beide volgens
hetzelfde fysicamechanisme gegenereerd worden. Meting en analyse van dergelijke
patronen bevestigen de hypothese van de Broglie in elk detail.




Next: De golffunctie
Up: GOLFKARAKTER VAN MATERIE
Previous: GOLFKARAKTER VAN MATERIE
Contents
Jo van den Brand
2004-09-25
![\includegraphics[width=12cm]{Figures/brag1.eps}](img424.png)
![\includegraphics[width=8cm]{Figures/Fig6a.eps}](img427.png)
![\includegraphics[width=8cm]{Figures/Fig6b.eps}](img428.png)