



Next: DEELTJES EN GOLVEN
Up: De golfvergelijking
Previous: De golfvergelijking
Contents
Stel dat de functie 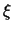 afhangt van zowel de plaats
afhangt van zowel de plaats  als de tijd
als de tijd 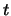 .
Als voorbeeld kiezen we de volgende golffunctie,
.
Als voorbeeld kiezen we de volgende golffunctie,
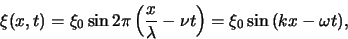 |
(66) |
met
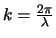 het golfgetal en
het golfgetal en
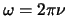 de hoekfrequentie. We kunnen nu de partiële afgeleide van
de hoekfrequentie. We kunnen nu de partiële afgeleide van 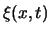 naar de plaats nemen, door aan te nemen dat de tijd hierbij een constante is.
We vinden
naar de plaats nemen, door aan te nemen dat de tijd hierbij een constante is.
We vinden
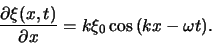 |
(67) |
Op analoge wijze vinden we
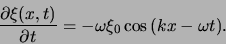 |
(68) |
De tweede-orde partiële afgeleiden kunnen nu ook worden bepaald en
we vinden
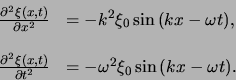 |
(69) |
We kunnen op deze wijze ook partiële afgeleiden nemen van andere functies.
Door invullen van de tweede-orde partiële afgeleiden
zien we direct dat de golffunctie gegeven door vergelijking (69)
voldoet aan de golfvergelijking (68) met als
voorwaarde
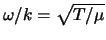 .
.




Next: DEELTJES EN GOLVEN
Up: De golfvergelijking
Previous: De golfvergelijking
Contents
Jo van den Brand
2004-09-25
![]() .
.