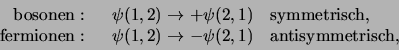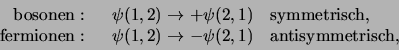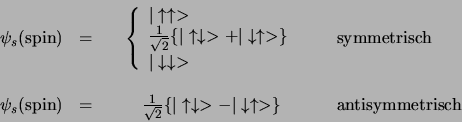Next: SYMMETRIEËN
Up: ELEMENTAIRE DEELTJES
Previous: Wisselwerking en deeltjesuitwisseling
Contents
Tenslotte zullen we in dit hoofdstuk ingaan op een wezenlijk
verschil tussen fermionen en bosonen39. Dit verschil heeft
te maken met de spin van het deeltje. Spin is een zuiver
quantummechanische eigenschap, die een maat is voor het
intrinsieke impulsmoment. Er is geen analogie in de
klassieke mechanica, alhoewel we ons dan vaak het deeltje voorstellen
als een snel rond zijn as draaiende tol. De grootte van de spin
(het is een vectorgrootheid) wordt uitgedrukt in eenheden van
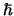 . De waarde
van de spin is, net als het baanimpulsmoment, gequantiseerd.
Deeltjes met halftallige
spin (
. De waarde
van de spin is, net als het baanimpulsmoment, gequantiseerd.
Deeltjes met halftallige
spin (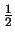 ,
, 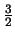 , enz.)
volgen Fermi-Dirac statistiek, terwijl deeltjes met
heeltallige spin (0, 1, enz.) voldoen aan Bose-Einstein statistiek. Dit
heeft tot gevolg dat de fermionen slechts in paren gecreëerd en
geannihileerd kunnen worden (bijvoorbeeld
, enz.)
volgen Fermi-Dirac statistiek, terwijl deeltjes met
heeltallige spin (0, 1, enz.) voldoen aan Bose-Einstein statistiek. Dit
heeft tot gevolg dat de fermionen slechts in paren gecreëerd en
geannihileerd kunnen worden (bijvoorbeeld
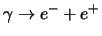 ).
Bosonen daarentegen kunnen in willekeurig aantal geproduceerd en geannihileerd
worden (bijvoorbeeld
).
Bosonen daarentegen kunnen in willekeurig aantal geproduceerd en geannihileerd
worden (bijvoorbeeld
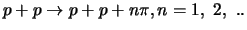 ), indien de
andere behoudswetten dat toestaan.
Het spin-statistiek theorema (
), indien de
andere behoudswetten dat toestaan.
Het spin-statistiek theorema (
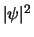 mag
niet veranderen) bepaalt nu dat voor de golffunctie
mag
niet veranderen) bepaalt nu dat voor de golffunctie 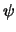 ,
van twee identieke deeltjes, moet gelden dat
,
van twee identieke deeltjes, moet gelden dat
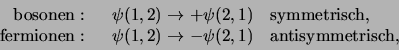 |
(660) |
in het geval dat beide deeltjes verwisseld worden.
Indien twee fermionen precies dezelfde quantumgetallen hebben,
en zich dus in dezelfde toestand bevinden, dan moet 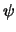 gelijk
zijn aan nul (het zogenaamde principe van Pauli). Daarentegen bezetten
meerdere bosonen `bij voorkeur' dezelfde toestand (zoals bijvoorbeeld
van toepassing is in een laser). Schrijven we de golffunctie van
twee deeltjes als een product van een plaatsgolffunctie en een
factor die de spinoriëntatie bepaalt,
gelijk
zijn aan nul (het zogenaamde principe van Pauli). Daarentegen bezetten
meerdere bosonen `bij voorkeur' dezelfde toestand (zoals bijvoorbeeld
van toepassing is in een laser). Schrijven we de golffunctie van
twee deeltjes als een product van een plaatsgolffunctie en een
factor die de spinoriëntatie bepaalt,
 |
(661) |
dan moet de totale golffunctie symmetrisch of
antisymmetrisch zijn. Indien de
plaatsgolffunctie als volgt geschreven kan worden,
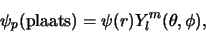 |
(662) |
waarbij 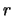 de afstand tussen beide deeltjes is en
de afstand tussen beide deeltjes is en 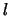 hun relatief
baanimpulsmoment, dan volgt bij verwisseling van de deeltjes in het
zwaartepunt,
hun relatief
baanimpulsmoment, dan volgt bij verwisseling van de deeltjes in het
zwaartepunt,
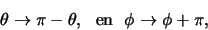 |
(663) |
en hiermee
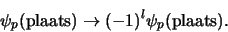 |
(664) |
De plaatsgolffunctie is dus symmetrisch voor even 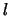 en
antisymmetrisch voor oneven
en
antisymmetrisch voor oneven 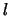 .
Bij identieke deeltjes moet dan de spingolffunctie, naar gelang
de deeltjessoort, symmetrisch of antisymmetrisch gekozen worden.
We krijgen bijvoorbeeld voor
.
Bij identieke deeltjes moet dan de spingolffunctie, naar gelang
de deeltjessoort, symmetrisch of antisymmetrisch gekozen worden.
We krijgen bijvoorbeeld voor
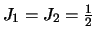 een symmetrische
golffunctie voor de triplettoestand (
een symmetrische
golffunctie voor de triplettoestand (
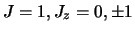 )
en een antisymmetrische golffunctie voor de singlettoestand
(
)
en een antisymmetrische golffunctie voor de singlettoestand
(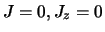 ).
).
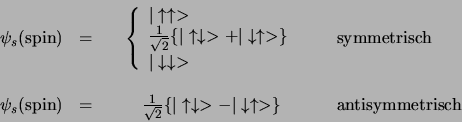 |
(665) |
Om het belang van symmetrieën te demonstreren, beschouwen we
het verval van een neutraal 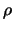 -meson in twee neutrale
pionen, dus
-meson in twee neutrale
pionen, dus
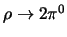 . De
. De 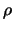 is een voorbeeld
van een vector meson, en zoals we later zullen zien
bezitten deze mesonen een spin
is een voorbeeld
van een vector meson, en zoals we later zullen zien
bezitten deze mesonen een spin 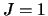 . De pionen zijn ongeladen en
dragen geen spin, en hun spingolffunctie,
. De pionen zijn ongeladen en
dragen geen spin, en hun spingolffunctie, 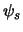 , is dan ook symmetrisch.
Omdat de pionen identieke bosonen zijn, dient hun totale
golffunctie symmetrisch te zijn, en er dient nu te gelden dat de
plaatsgolffunctie,
, is dan ook symmetrisch.
Omdat de pionen identieke bosonen zijn, dient hun totale
golffunctie symmetrisch te zijn, en er dient nu te gelden dat de
plaatsgolffunctie, 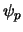 , symmetrisch is. Dit betekent dat
de gecreëerde pionen een even totaal-impulsmoment dienen
te hebben. Omdat we een
, symmetrisch is. Dit betekent dat
de gecreëerde pionen een even totaal-impulsmoment dienen
te hebben. Omdat we een 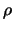 meson met spin
meson met spin 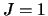 in de begintoestand hebben, is het verval dus verboden door
de wet van behoud van impulsmoment en Bose-symmetrie.
in de begintoestand hebben, is het verval dus verboden door
de wet van behoud van impulsmoment en Bose-symmetrie.




Next: SYMMETRIEËN
Up: ELEMENTAIRE DEELTJES
Previous: Wisselwerking en deeltjesuitwisseling
Contents
Jo van den Brand
2004-09-25