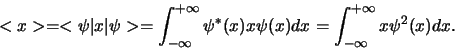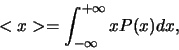Next: De onzekerheidsrelaties van Heisenberg
Up: Grondslagen van de quantummechanica
Previous: Axiomas
Contents
We dienen nu enkel nog te weten wat de operatoren zijn die corresponderen
met de desbetreffende fysische grootheden. Helaas kunnen deze niet algemeen
afgeleid worden en dient men analogiën te gebruiken. De juiste operator
is die, waarvoor men in het grensgeval met de klassieke mechanica de
bekende klassieke resultaten verkrijgt. Dergelijke analogiën worden
bijzonder duidelijk indien men de klassieke mechanica uitdrukt
in het Hamilton en Lagrange formalisme (hetgeen we hier niet zullen doen).
Op deze wijze vindt men dat de operator van de positie  overeenkomt
met het vermenigvuldigen met de variabele
overeenkomt
met het vermenigvuldigen met de variabele  ,
,
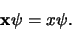 |
(348) |
De operator van de impulscomponent 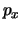 correspondeert met de
partiële afgeleide naar
correspondeert met de
partiële afgeleide naar  ,
,
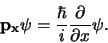 |
(349) |
We vragen ons af hoe de toestanden er uitzien, waarvoor de deeltjes
een scherpe waarde van de impulscomponent 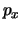 hebben. In dat geval
dient hun toestandsfunctie
hebben. In dat geval
dient hun toestandsfunctie 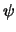 een eigenfunctie van de impulsoperator
zijn,
een eigenfunctie van de impulsoperator
zijn,
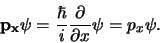 |
(350) |
Enkel een exponentiële functie is evenredig met zijn eigen afgeleide
en daarom wordt een toestand met scherp gedefinieerde impuls
geschreven als
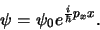 |
(351) |
Het reële deel hiervan is een harmonische golf die geschreven
kan worden als
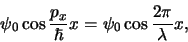 |
(352) |
waarbij de golflengte gelijk is aan
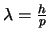 zoals
vereist door de Broglie. Enkel harmonische
zoals
vereist door de Broglie. Enkel harmonische 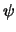 golven hebben
een scherp bepaalde impuls. Nuttig is de afkorting
golven hebben
een scherp bepaalde impuls. Nuttig is de afkorting
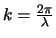 ,
met
,
met 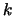 het golfgetal, waarmee de impulseigenfunctie geschreven kan
worden als
het golfgetal, waarmee de impulseigenfunctie geschreven kan
worden als
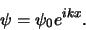 |
(353) |
Het is iets gecompliceerder om de vraag te beantwoorden welke toestanden
corresponderen met een deeltje dat zich
op een scherp bepaalde positie bevindt, bijvoorbeeld
op positie 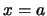 . In dat geval dient
. In dat geval dient 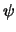 een eigenfunctie van de
plaatsoperator te zijn,
een eigenfunctie van de
plaatsoperator te zijn,
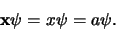 |
(354) |
Hierbij dient vermenigvuldigen met de variabele  overeen te komen
met vermenigvuldigen met de constante
overeen te komen
met vermenigvuldigen met de constante 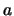 . Als we dat proberen, dan
vinden we dat hiervoor de functie
. Als we dat proberen, dan
vinden we dat hiervoor de functie 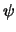 overal gelijk
aan nul dient te zijn, behalve bij
overal gelijk
aan nul dient te zijn, behalve bij 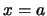 ! Deze functie, die overal nul is behalve
op de positie
! Deze functie, die overal nul is behalve
op de positie 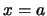 , waar ze oneindig is, heet de
, waar ze oneindig is, heet de 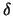 -functie.
Men kan zich deze functie voorstellen als bijvoorbeeld een
Gaussverdeling waarvan de breedte steeds kleiner wordt, maar waarvan het maximum
tegelijkertijd steeds hoger wordt. Indien
-functie.
Men kan zich deze functie voorstellen als bijvoorbeeld een
Gaussverdeling waarvan de breedte steeds kleiner wordt, maar waarvan het maximum
tegelijkertijd steeds hoger wordt. Indien 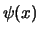 geen
geen 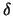 -functie
is, dan heeft
-functie
is, dan heeft  geen scherpe waarde en kan het deeltje zich overal
bevinden. Volgens de axiomas van de quantummechanica wordt de
meest waarschijnlijke positie dan gegeven door
geen scherpe waarde en kan het deeltje zich overal
bevinden. Volgens de axiomas van de quantummechanica wordt de
meest waarschijnlijke positie dan gegeven door
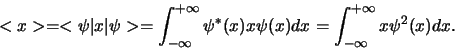 |
(355) |
Deze vergelijking ziet er hetzelfde uit die voor de gemiddelde waarde
van een grootheid  , waarvan we enkel de waarschijnlijkheidsverdeling
, waarvan we enkel de waarschijnlijkheidsverdeling
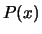 kennen,
kennen,
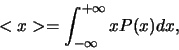 |
(356) |
indien we ervan uitgaan dat 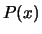 op de juiste wijze genormeerd is.
Dan geldt namelijk dat
op de juiste wijze genormeerd is.
Dan geldt namelijk dat
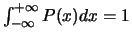 .
Men kan
.
Men kan 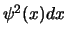 dus interpreteren als de
waarschijnlijkheid13 dat bij een meting
het deeltje in het interval tussen
dus interpreteren als de
waarschijnlijkheid13 dat bij een meting
het deeltje in het interval tussen  en
en 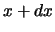 zou worden aangetroffen.
zou worden aangetroffen.




Next: De onzekerheidsrelaties van Heisenberg
Up: Grondslagen van de quantummechanica
Previous: Axiomas
Contents
Jo van den Brand
2004-09-25
![]() . In dat geval dient
. In dat geval dient ![]() een eigenfunctie van de
plaatsoperator te zijn,
een eigenfunctie van de
plaatsoperator te zijn,