De eigenfuncties van een Hermitische operator hebben de belangrijke
eigenschap dat ze een orthonormaal stelsel vormen. Er geldt
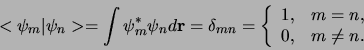 |
(337) |
Een andere belangrijke eigenschap van Hermitische operatoren is dat
de verzameling eigenfuncties,
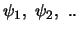 , een complete
set vormen. Dit betekent dat een willekeurige toestandsfunctie
, een complete
set vormen. Dit betekent dat een willekeurige toestandsfunctie 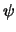 van het systeem geëxpandeerd kan worden in termen van de
eigenfuncties van een willekeurige Hermitische operator als
van het systeem geëxpandeerd kan worden in termen van de
eigenfuncties van een willekeurige Hermitische operator als
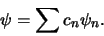 |
(338) |
Indien we bovenstaande vergelijking vermenigvuldigen met 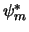 en vervolgens integreren, waarbij we gebruik maken
van de orthonormaliteitsrelaties,
dan verkrijgen we voor de expansiecoëfficienten
en vervolgens integreren, waarbij we gebruik maken
van de orthonormaliteitsrelaties,
dan verkrijgen we voor de expansiecoëfficienten
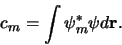 |
(339) |
Met behulp van het expansietheorema (vergelijking (342)), kunnen we de
waarschijnlijkheidsverdeling afleiden voor de resultaten van metingen
van 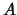 . De verwachtingswaarde van de observabele
. De verwachtingswaarde van de observabele 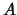 voor een
systeem beschreven door toestand
voor een
systeem beschreven door toestand 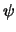 wordt gegeven door
wordt gegeven door
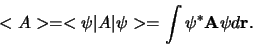 |
(340) |
Indien we gebruik maken van het expansietheorema,
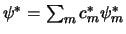 en
en
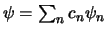 ,
dan vinden we
,
dan vinden we
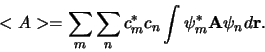 |
(341) |
Vervolgens maken we gebruik van de eigenwaardenvergelijking
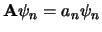 en vinden
en vinden
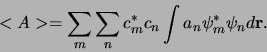 |
(342) |
Tenslotte gebruiken we de orthonormaliteitsrelaties
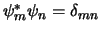 en verkrijgen
en verkrijgen
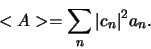 |
(343) |
Hieruit concluderen we dat voor een systeem in toestand 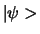 een
meting van de grootheid
een
meting van de grootheid 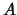 de waarde
de waarde 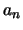 levert met een waarschijnlijkheid
levert met een waarschijnlijkheid
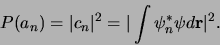 |
(344) |
Uit de normering van de toestandsfunctie volgt dat
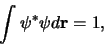 |
(345) |
en als we nu gebruik maken van het expansietheorema en de
orthonormaliteits relaties, dan vinden we
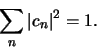 |
(346) |
In dat geval geldt dus ook
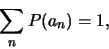 |
(347) |
waaruit we concluderen dat de enige mogelijke
waarden die verkregen kunnen worden bij een meting van de observabele
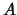 , de eigenwaarden
, de eigenwaarden
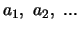 zijn.
zijn.
We komen dus tot de opmerkelijke conclusie dat in welke toestand
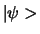 het systeem ook is, als resultaat van een meting
kunnen enkel eigenwaarden zoals
het systeem ook is, als resultaat van een meting
kunnen enkel eigenwaarden zoals 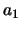 en
en 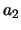 gevonden worden en niet bijvoorbeeld een waarde tussen
gevonden worden en niet bijvoorbeeld een waarde tussen
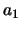 en
en 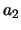 . Dit is volledig anders dan we op basis van de klassieke
fysica zouden verwachten. Dit gedrag is volledig in overeenstemming met
experimentele resultaten.
. Dit is volledig anders dan we op basis van de klassieke
fysica zouden verwachten. Dit gedrag is volledig in overeenstemming met
experimentele resultaten.
![]() en
en ![]() geldt dat
geldt dat
![\begin{displaymath}
\sum_{m,n=1}^2 c_m^* c_n \left[ \int \psi_m^* {\bf A} \psi_...
...bf r} -
\int ({\bf A} \psi_m)^* \psi_n d{\bf r} \right] = 0
\end{displaymath}](img1098.png)
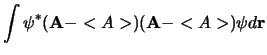
![$\displaystyle \int \left[ ( {\bf A} - <A> ) \psi \right]^*
\left[ ({\bf A} - < A>)\psi \right] d{\bf r}$](img1103.png)
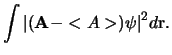
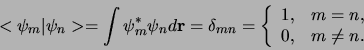
![]() , een complete
set vormen. Dit betekent dat een willekeurige toestandsfunctie
, een complete
set vormen. Dit betekent dat een willekeurige toestandsfunctie ![]() van het systeem geëxpandeerd kan worden in termen van de
eigenfuncties van een willekeurige Hermitische operator als
van het systeem geëxpandeerd kan worden in termen van de
eigenfuncties van een willekeurige Hermitische operator als
![]() . De verwachtingswaarde van de observabele
. De verwachtingswaarde van de observabele ![]() voor een
systeem beschreven door toestand
voor een
systeem beschreven door toestand ![]() wordt gegeven door
wordt gegeven door
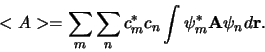
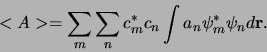
![]() het systeem ook is, als resultaat van een meting
kunnen enkel eigenwaarden zoals
het systeem ook is, als resultaat van een meting
kunnen enkel eigenwaarden zoals ![]() en
en ![]() gevonden worden en niet bijvoorbeeld een waarde tussen
gevonden worden en niet bijvoorbeeld een waarde tussen
![]() en
en ![]() . Dit is volledig anders dan we op basis van de klassieke
fysica zouden verwachten. Dit gedrag is volledig in overeenstemming met
experimentele resultaten.
. Dit is volledig anders dan we op basis van de klassieke
fysica zouden verwachten. Dit gedrag is volledig in overeenstemming met
experimentele resultaten.