



Next: ELEMENTAIRE DEELTJES
Up: TIJDAFHANKELIJKE STORINGSREKENING
Previous: Levensduur van een aangeslagen
Contents
De `collapse' van de golffunctie is zonder twijfel een opzienbarend
ingrediënt in de quantum fysica. Het concept is geïntroduceerd
op zuiver theoretische gronden om het feit te verklaren dan onmiddellijk
herhaalde metingen hetzelfde resultaat dienen te leveren.
Misra en Sudashan21 hebben in 1977 wat zij het quantum
Zeno effect noemen, voorgesteld als een dramatische experimentele
demonstratie van de `collapse' van de golffunctie. Het was hun idee
om een onstabiel systeem, bijvoorbeeld een atoom in een aangeslagen
toestand, te nemen en dit te onderwerpen aan herhaalde metingen.
Elke observatie zorgt voor een `collapse' van de golffunctie, waardoor
de klok gereset wordt. Hierdoor is het mogelijk om het verwachte
verval van het systeem naar een lagere toestand oneindig lang
uit te stellen.
Stel dat een systeem begint in de aangeslagen toestand 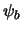 , dat
een natuurlijke levensduur
, dat
een natuurlijke levensduur 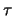 heeft voor de overgang naar
de grondtoestand
heeft voor de overgang naar
de grondtoestand 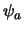 . Normaal gesproken, voor tijden die significant
korter zijn dan
. Normaal gesproken, voor tijden die significant
korter zijn dan 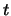 , volgt uit vergelijking (636) dat
de overgangswaarschijnlijkheid evenredig is met
, volgt uit vergelijking (636) dat
de overgangswaarschijnlijkheid evenredig is met 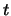 .
In feite, omdat de overgangssnelheid gelijk is aan
.
In feite, omdat de overgangssnelheid gelijk is aan 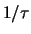 , zie
vergelijkingen (641) en (644), geldt
, zie
vergelijkingen (641) en (644), geldt
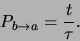 |
(634) |
Als een meting uitvoeren op tijdstip 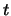 , dan is de waarschijnlijkheid
dat het systeem zich nog steeds in de aangeslagen toestand bevindt gelijk aan
, dan is de waarschijnlijkheid
dat het systeem zich nog steeds in de aangeslagen toestand bevindt gelijk aan
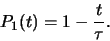 |
(635) |
Stel nu dat we het systeem inderdaad in de aangeslagen toestand aantreffen.
In dat geval `collapsed' de golffunctie terug naar 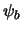 en
het hele proces begint opnieuw. Als we een tweede meting uitvoeren,
op tijdstip
en
het hele proces begint opnieuw. Als we een tweede meting uitvoeren,
op tijdstip 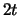 , dan is de waarschijnlijkheid om het systeem nog steeds
in de aangeslagen toestand aan te treffen
, dan is de waarschijnlijkheid om het systeem nog steeds
in de aangeslagen toestand aan te treffen
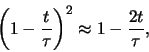 |
(636) |
hetgeen hetzelfde is als wanneer we de meting op tijdstip 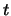 niet
zouden hebben uitgevoerd. Dit is zeker wat men ook naief zou
verwachten. Als dit het hele verhaal zou zijn, dan zijn we er
niets mee opgeschoten door metingen aan het systeem uit te voeren.
In dat geval zou er geen quantum Zeno effect bestaan.
niet
zouden hebben uitgevoerd. Dit is zeker wat men ook naief zou
verwachten. Als dit het hele verhaal zou zijn, dan zijn we er
niets mee opgeschoten door metingen aan het systeem uit te voeren.
In dat geval zou er geen quantum Zeno effect bestaan.
Het is echter zo dat voor extreem korte tijden, de
overgangswaarschijnlijkheid niet evenredig is met 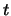 ,
maar met
,
maar met 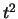 . Dit volgt uit vergelijking (633)
voor kleine
. Dit volgt uit vergelijking (633)
voor kleine 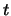 en we vinden
en we vinden
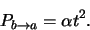 |
(637) |
Merk op dat we in onze afleiding om een lineaire tijdafhankelijk
te krijgen, hebben aangenomen dat de functie
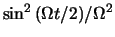 in vergelijking (633)
een scherpe piek was. Echter, de breedte van deze piek is
van de orde
in vergelijking (633)
een scherpe piek was. Echter, de breedte van deze piek is
van de orde
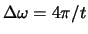 en voor extreem korte
en voor extreem korte
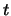 geldt deze benadering niet en gaat de integraal over in
geldt deze benadering niet en gaat de integraal over in
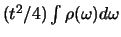 .
In dit geval is de waarschijnlijkheid om het systeem na
twee metingen nog steeds in de aangeslagen toestand aan te treffen
gelijk aan
.
In dit geval is de waarschijnlijkheid om het systeem na
twee metingen nog steeds in de aangeslagen toestand aan te treffen
gelijk aan
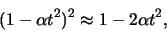 |
(638) |
terwijl dit, wanneer we de eerste meting niet zouden hebben uitgevoerd,
zou moeten zijn
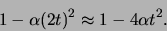 |
(639) |
Klaarblijkelijk heeft onze eerste meting aan het systeem op tijdstip 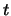 de netto overgangswaarschijnlijkheid naar de grondtoestand
verminderd!
de netto overgangswaarschijnlijkheid naar de grondtoestand
verminderd!
Het is inderdaad zo dat wanneer we 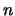 metingen uitvoeren
gedurende de periode van
metingen uitvoeren
gedurende de periode van 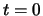 tot
tot 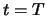 (we maken dus
metingen op tijdstippen
(we maken dus
metingen op tijdstippen
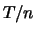 ,
, 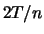 ,
, 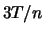 , ...,
, ..., 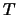 ), de waarschijnlijkheid
om aan het eind het systeem nog steeds in de aangeslagen toestand
aan te treffen, gelijk aan
), de waarschijnlijkheid
om aan het eind het systeem nog steeds in de aangeslagen toestand
aan te treffen, gelijk aan
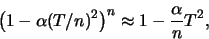 |
(640) |
en dit wordt gelijk aan 1 in de limiet
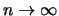 .
Dit betekent dat een continue geobserveerd onstabiel systeem
nooit zal vervallen!
.
Dit betekent dat een continue geobserveerd onstabiel systeem
nooit zal vervallen!




Next: ELEMENTAIRE DEELTJES
Up: TIJDAFHANKELIJKE STORINGSREKENING
Previous: Levensduur van een aangeslagen
Contents
Jo van den Brand
2004-09-25
![]() , dat
een natuurlijke levensduur
, dat
een natuurlijke levensduur ![]() heeft voor de overgang naar
de grondtoestand
heeft voor de overgang naar
de grondtoestand ![]() . Normaal gesproken, voor tijden die significant
korter zijn dan
. Normaal gesproken, voor tijden die significant
korter zijn dan ![]() , volgt uit vergelijking (636) dat
de overgangswaarschijnlijkheid evenredig is met
, volgt uit vergelijking (636) dat
de overgangswaarschijnlijkheid evenredig is met ![]() .
In feite, omdat de overgangssnelheid gelijk is aan
.
In feite, omdat de overgangssnelheid gelijk is aan ![]() , zie
vergelijkingen (641) en (644), geldt
, zie
vergelijkingen (641) en (644), geldt
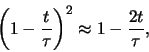
![]() ,
maar met
,
maar met ![]() . Dit volgt uit vergelijking (633)
voor kleine
. Dit volgt uit vergelijking (633)
voor kleine ![]() en we vinden
en we vinden
![]() metingen uitvoeren
gedurende de periode van
metingen uitvoeren
gedurende de periode van ![]() tot
tot ![]() (we maken dus
metingen op tijdstippen
(we maken dus
metingen op tijdstippen
![]() ,
, ![]() ,
, ![]() , ...,
, ..., ![]() ), de waarschijnlijkheid
om aan het eind het systeem nog steeds in de aangeslagen toestand
aan te treffen, gelijk aan
), de waarschijnlijkheid
om aan het eind het systeem nog steeds in de aangeslagen toestand
aan te treffen, gelijk aan