Next: Spontane emissie
Up: Emissie en absorptie van
Previous: Absorptie, gestimuleerde emissie, en
Contents
De energiedichtheid van een elektromagnetische golf wordt
gegeven door
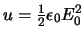 , met
, met 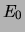 de
amplitude van het elektrische veld. De overgangswaarschijnlijkheid
gegeven in vergelijking (631) is evenredig met de
energiedichtheid van de velden,
de
amplitude van het elektrische veld. De overgangswaarschijnlijkheid
gegeven in vergelijking (631) is evenredig met de
energiedichtheid van de velden,
![\begin{displaymath}
P_{b \rightarrow a} (t)
= {2u \over \epsilon_0 \hbar^2} \...
..._0 - \omega )t/2 \right]}
\over ( \omega_0 - \omega )^2} .
\end{displaymath}](img1765.png) |
(621) |
Bovenstaand resultaat geldt echter alleen voor een monochromatische
verstoring, die uit een enkele frequentie 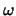 bestaat.
In veel toepassingen wordt het atoom blootgesteld aan elektromagnetische
golven die een heel spectrum van frequenties hebben. In dat
geval geldt
bestaat.
In veel toepassingen wordt het atoom blootgesteld aan elektromagnetische
golven die een heel spectrum van frequenties hebben. In dat
geval geldt
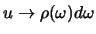 , waarbij
, waarbij
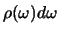 de energiedichtheid in het frequentie gebied
de energiedichtheid in het frequentie gebied
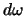 is. De overgangswaarschijnlijkheid neemt dan de volgende vorm aan,
is. De overgangswaarschijnlijkheid neemt dan de volgende vorm aan,
![\begin{displaymath}
P_{b \rightarrow a} (t)
= {2u \over \epsilon_0 \hbar^2} \...
...\right]}
\over ( \omega_0 - \omega )^2} \right\} d\omega .
\end{displaymath}](img1769.png) |
(622) |
In het algemeen zal de term tussen de accoladen scherp gepiekt zijn
rond de frequentie 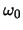 , terwijl
, terwijl
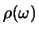 een relatief
brede verdeling heeft. In dat geval mogen we
een relatief
brede verdeling heeft. In dat geval mogen we
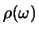 vervangen door
vervangen door
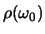 en dit buiten de integraal halen.
We vinden
en dit buiten de integraal halen.
We vinden
![\begin{displaymath}
P_{b \rightarrow a} (t)
= {2u \vert {\mathcal{P}} \vert^2...
...\right]}
\over ( \omega_0 - \omega )^2} \right\} d\omega .
\end{displaymath}](img1772.png) |
(623) |
Als we de variabelen veranderen in
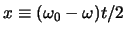 en de
integraalgrenzen vervangen door
en de
integraalgrenzen vervangen door
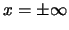 (de integraal is
toch praktisch gelijk aan nul in dat gebied), vinden we een
standaardvorm voor de bepaalde integraal,
(de integraal is
toch praktisch gelijk aan nul in dat gebied), vinden we een
standaardvorm voor de bepaalde integraal,
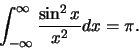 |
(624) |
We vinden hiermee
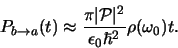 |
(625) |
De overgangswaarschijnlijkheid is evenredig met 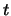 . Het bizarre
`flip-flop' gedrag van een monochromatische verstoring is `verwaterd'
nu we het systeem aanslaan met een incoherent spectrum van
frequenties. In het bijzonder is de overgangssnelheid,
. Het bizarre
`flip-flop' gedrag van een monochromatische verstoring is `verwaterd'
nu we het systeem aanslaan met een incoherent spectrum van
frequenties. In het bijzonder is de overgangssnelheid,
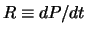 nu een constante,
nu een constante,
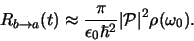 |
(626) |
Tot nu toe hebben we aangenomen dat de verstorende golf invalt langs
de  -richting en gepolariseerd is langs de
-richting en gepolariseerd is langs de  -richting. Voor een
atoom dat zich in een `bad' van fotonen bevindt, die van alle kanten
komen en alle mogelijke polarisaties hebben, vinden we
-richting. Voor een
atoom dat zich in een `bad' van fotonen bevindt, die van alle kanten
komen en alle mogelijke polarisaties hebben, vinden we
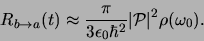 |
(627) |
Dit is de overgangssnelheid voor gestimuleerde emissie van toestand
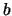 naar
naar 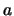 onder invloed van incoherente, ongepolariseerd licht,
dat van alle kanten invalt. Hierbij is
onder invloed van incoherente, ongepolariseerd licht,
dat van alle kanten invalt. Hierbij is 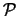 het matrixelement
van het elektrisch dipoolmoment tussen de twee toestanden en
het matrixelement
van het elektrisch dipoolmoment tussen de twee toestanden en
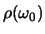 is de energiedichtheid van de velden, per
eenheid frequentie, berekend voor
is de energiedichtheid van de velden, per
eenheid frequentie, berekend voor
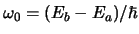 .
.




Next: Spontane emissie
Up: Emissie en absorptie van
Previous: Absorptie, gestimuleerde emissie, en
Contents
Jo van den Brand
2004-09-25
![\begin{displaymath}
P_{b \rightarrow a} (t)
= {2u \over \epsilon_0 \hbar^2} \...
..._0 - \omega )t/2 \right]}
\over ( \omega_0 - \omega )^2} .
\end{displaymath}](img1765.png)