



Next: Levensduur van een aangeslagen
Up: Emissie en absorptie van
Previous: Incoherente verstoringen
Contents
Stel dat we een vat atomen hebben, waarvan er zich 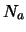 in de
grondtoestand bevinden en
in de
grondtoestand bevinden en 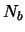 in de aangeslagen toestand.
We noemen
in de aangeslagen toestand.
We noemen 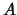 de snelheid voor spontane emissie, zodat het
aantal deeltjes dat de aangeslagen toestand verlaat ten gevolge
hiervan, gelijk is aan
de snelheid voor spontane emissie, zodat het
aantal deeltjes dat de aangeslagen toestand verlaat ten gevolge
hiervan, gelijk is aan 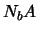 . De overgangssnelheid voor
gestimuleerde emissie noemen we
. De overgangssnelheid voor
gestimuleerde emissie noemen we
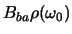 en
wordt gegeven door
vergelijking (638). Deze snelheid is evenredig met de
energiedichtheid van het elektromagnetische veld.
Het aantal deeltjes dat per seconde de aangeslagen toestand verlaat door
gestimuleerde emissie is dus
en
wordt gegeven door
vergelijking (638). Deze snelheid is evenredig met de
energiedichtheid van het elektromagnetische veld.
Het aantal deeltjes dat per seconde de aangeslagen toestand verlaat door
gestimuleerde emissie is dus
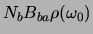 .
De snelheid van absorptie is ook evenredig met
.
De snelheid van absorptie is ook evenredig met
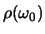 en we noemen het
en we noemen het
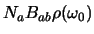 . Er geldt
. Er geldt
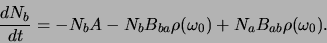 |
(628) |
De afgeleide is gelijk aan nul als er evenwicht heerst en we
vinden dan
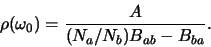 |
(629) |
Als we nu verder Boltzmann statistiek en de stralingswet van Planck
beschouwen, kunnen we concluderen dat de overgangssnelheid
voor spontane emissie gelijk is aan
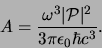 |
(630) |




Next: Levensduur van een aangeslagen
Up: Emissie en absorptie van
Previous: Incoherente verstoringen
Contents
Jo van den Brand
2004-09-25