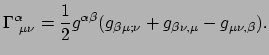- ...i1
- Galileo Galileï heeft een belangrijke
invloed op de ontwikkeling van wetenschap gehad: hij was van mening
dat wetenschap gebaseerd diende te zijn op zorgvulding experimenteel
onderzoek. Ook beschreef hij waarnemingen wiskundig.
Hij formuleerde het equivalentieprincipe, liet zien dat de versnelling
van de zwaartekracht uniform is (
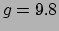 m/s
m/s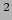 ), toonde dat horizontale
en verticale bewegingen afzonderlijk beschreven kunnen worden, en gaf ons
het principe van relativiteit. Galileï was hiermee de eerste relativist.
), toonde dat horizontale
en verticale bewegingen afzonderlijk beschreven kunnen worden, en gaf ons
het principe van relativiteit. Galileï was hiermee de eerste relativist.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
inertiaalsystemen2
- Het referentiesysteem dat verbonden is met het
oppervlak van de aarde is niet helemaal een inertiaal referentiesysteem, omdat
er een kleine versnelling is van het aardoppervlak ten gevolge van de rotatie
van de aarde, alsook een versnelling ten gevolge van de beweging rond de zon.
Deze versnellingen zijn kleiner dan
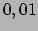 m/s
m/s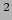 en kunnen vaak worden
verwaarloosd.
en kunnen vaak worden
verwaarloosd.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... maken3
- Dit kan ook begrepen worden uit een
gedachtenexperiment van toegeschreven aan Galileï. Stel dat zware voorwerpen
sneller vallen dan lichte voorwerpen. We binden vervolgens een lichte kogel vast aan
een zware en gooien het stel naar beneden van de toren van Pisa. Nu zal de lichte kogel
de zware afremmen en de combinatie valt langszamer dan de zware kogel
alleen zou vallen. De combinatie is echter zwaarder dan enkel de zware kogel
en zou dus sneller moeten vallen. Ergo, contradictio in terminis.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... voeren4
- Simon Stevin heeft reeds in 1586 zijn experiment
gepubliceerd waarin hij twee loden ballen, een tien keer zwaarder dan de ander, van
de klokkentoren van de oude kerk in Delft heeft laten vallen over een afstand van ongeveer 10 m.
Hierbij werd geen verschil waargenomen in tegenstelling tot de bewering van
aanhangers van Aristoteles.
Zijn publicatie was drie jaar vóór Galileï's eerste behandeling van gravitatie
en 18 jaar eerder dan Galileï's theoretisch werk over vallende lichamen.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
5
- Een dergelijk experiment is door astronaut
David Scott uitgevoerd op de maan met een hamer en veer tijdens de Apollo 15 missie.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... licht6
- We weten dat licht een bijzondere plaats
inneemt in Einstein's relativiteitstheorie: de snelheid van licht is een universele
constante in elk referentiesysteem, terwijl licht een inertiale massa heeft die
gelijk is aan nul. We kunnen daarom niet eenvoudig de wet
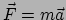 gebruiken om de beweging van licht te beschrijven.
gebruiken om de beweging van licht te beschrijven.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... Dopplerverschuiving7
- In het geval van
geluidsgolven zorgt het Dopplereffect voor een verschuiving naar hogere
frequentie van de toon van de sirene van een naderende ziekenwagen, terwijl de toon
naar lagere frequenties verschuift als de ziekenwagen van ons af beweegt.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... waarnemer8
- Evenzo
voelen wij de beweging van de aarde rond de zon niet, omdat de aarde in
vrije val is en er dus niets te voelen valt.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
bepalen9
- Relatie (9) kan ook gevonden worden door
twee experimentatoren in een ruimteschip te beschouwen, dat reist
met constante versnelling
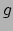 . De afstand tussen de twee waarnemers is
. De afstand tussen de twee waarnemers is 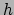 in
de richting van de versnelling. Laten we aannemen dat het ruimteschip in rust
is ten opzichte van een bepaald inertiaalsysteem op het moment dat de waarnemer
beneden (bron) een foton uitzendt. Het duurt tijd
in
de richting van de versnelling. Laten we aannemen dat het ruimteschip in rust
is ten opzichte van een bepaald inertiaalsysteem op het moment dat de waarnemer
beneden (bron) een foton uitzendt. Het duurt tijd 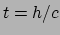 voordat dit foton bij de
bovenste (top) waarnemer aankomt. Op dat moment heeft deze waarnemer een
snelheid
voordat dit foton bij de
bovenste (top) waarnemer aankomt. Op dat moment heeft deze waarnemer een
snelheid
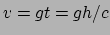 en neemt hij het foton waar met een Dopplerverschuiving,
precies volgens vergelijking (9). Het equivalentieprincipe
eist dat, indien deze roodverschuiving wordt waargenomen in een experiment
dat wordt uitgevoerd onder condities van uniforme versnelling in afwezigheid
van een gravitatieveld, dezelfde roodverschuiving waargenomen dient te worden in een
experiment onder condities van een uniform gravitatieveld, maar zonder versnelling.
en neemt hij het foton waar met een Dopplerverschuiving,
precies volgens vergelijking (9). Het equivalentieprincipe
eist dat, indien deze roodverschuiving wordt waargenomen in een experiment
dat wordt uitgevoerd onder condities van uniforme versnelling in afwezigheid
van een gravitatieveld, dezelfde roodverschuiving waargenomen dient te worden in een
experiment onder condities van een uniform gravitatieveld, maar zonder versnelling.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... roodverschuiving10
- Waarnemen van een gravitationele
roodverschuiving heeft ook als directe consequentie dat ruimtetijd
gekromd dient te zijn.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
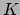 11
11
- We kunnen de formule voor de kinetische
energie
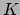 vinden door de arbeid te beschouwen die verricht moet worden om
een deeltje gedurende tijd
vinden door de arbeid te beschouwen die verricht moet worden om
een deeltje gedurende tijd 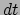 te versnellen. Er geldt
te versnellen. Er geldt
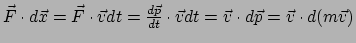 . Ook geldt
. Ook geldt
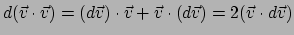 . Aannemende dat de massa constant is vinden
we hiermee
. Aannemende dat de massa constant is vinden
we hiermee
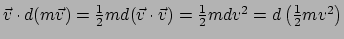 . Integreren hiervan
levert de relatie
. Integreren hiervan
levert de relatie
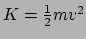 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
(AU)12
- De astronomische eenheid was vroeger gedefinieerd als de straal van
de cirkelbaan van de aarde (in 1900) rond de zon: 1 AU =
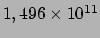 m.
m.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... aarde13
- De getijdenkrachten van de maan
op de aarde proberen ook de rotatie van de aarde te synchroniseren met de
omlooptijd van de maan. De aarde is echter veel massiever dan de maan. Ongeveer
1 miljard jaar geleden duurde een dag maar ongeveer 18 uur.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... Newton14
- Enkele redenen zijn dat in het
formalisme van Lagrange de belangrijkste functie een scalair is, waar in
de tweede wet van Newton vectoren voorkomen. Ook is het zo dat bepaalde
symmetrie-eigenschappen van fysische systemen zich vaak duidelijk openbaren
in het Lagrange-formalisme. Het is om deze redenen dat in onder andere
de quantumveldentheorie vrijwel uitsluitend met Lagrangianen gewerkt wordt.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... door15
- De
notatie
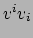 betekent in bovenstaand geval
betekent in bovenstaand geval
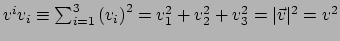 . Het betreft de zogenaamde Einstein sommatieconventie
die we later veelvuldig zullen gebruiken.
. Het betreft de zogenaamde Einstein sommatieconventie
die we later veelvuldig zullen gebruiken.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... door16
- Dit
is gebaseerd op een
eerste-orde Taylorreeks van
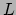 rond de waarden
rond de waarden 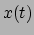 en
en 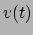 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
integratie17
- Stel dat
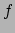 en
en 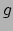 functies zijn van
functies zijn van 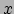 , dus
, dus 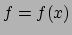 en
en 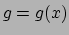 . Dan geldt voor de afgeleide van het product
. Dan geldt voor de afgeleide van het product
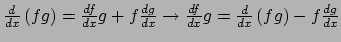 . Integreren
over
. Integreren
over 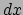 levert
levert
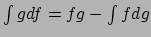 . In vergelijking (32) gebruiken
we
. In vergelijking (32) gebruiken
we
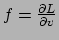 en
en
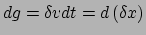 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... lichamen...'18
- A. Einstein in een brief naar Ernst Mach,
Zürich, 25 Juni 1923.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... lengte19
- Naar de Britse astrofysicus Sir James Jeans
(1877 - 1946). We kunnen de grootte
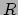 van een sferisch gebied dat instabiel
is voor stervorming bij benadering vinden door de gemiddelde kinetische energie
van een sferisch gebied dat instabiel
is voor stervorming bij benadering vinden door de gemiddelde kinetische energie
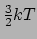 van een molecuul met massa
van een molecuul met massa 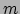 gelijk te stellen aan de
absolute waarde van de gravitationele potentiële energie
gelijk te stellen aan de
absolute waarde van de gravitationele potentiële energie
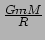 .
Vervolgens vervangen we de massa
.
Vervolgens vervangen we de massa 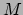 van dit gebied door haar dichtheid
van dit gebied door haar dichtheid
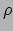 via de substitutie
via de substitutie
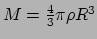 . Dit levert dan de benadering
. Dit levert dan de benadering
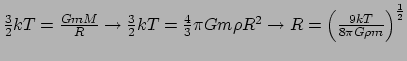 .
Een exacte berekening die de geluidssnelheid in de gaswolk in rekening brengt,
levert vergelijking (38).
.
Een exacte berekening die de geluidssnelheid in de gaswolk in rekening brengt,
levert vergelijking (38).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... warmte20
- Ook onze zon is uit een dergelijke
protoster ontstaan. De zon heeft een massa
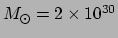 kg en
bestaat uit ongeveer
kg en
bestaat uit ongeveer 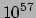 waterstofatomen met elk een massa van
waterstofatomen met elk een massa van
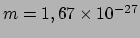 kg. De huidige luminositeit van de zon bedraagt
kg. De huidige luminositeit van de zon bedraagt
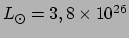 W. We hebben gezien dat de ontsnappingssnelheid
van de zon gelijk is aan
W. We hebben gezien dat de ontsnappingssnelheid
van de zon gelijk is aan
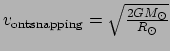 .
De kinetische energie van een atoom als het de zon bereikt is dus
.
De kinetische energie van een atoom als het de zon bereikt is dus
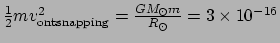 J.
Hieruit volgt dat de gravitationele potentiële energie voldoende is om de
protoster enkele miljoenen jaren te laten schijnen.
J.
Hieruit volgt dat de gravitationele potentiële energie voldoende is om de
protoster enkele miljoenen jaren te laten schijnen.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
doorsneden21
- De werkzame doorsnede is een
maat voor de waarschijnlijkheid dat een bepaalde wisselwerking tussen deeltjes plaatsvindt
(bijvoorbeeld verstrooiing of een kernreactie). Deze waarschijnlijkheid is vaak sterk afhankelijk
van de energie van de deeltjes of de samenstelling van een target dat wordt beschoten.
De werkzame doorsnede wordt aangeduid met
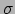 en heeft de dimensie van oppervlakte.
en heeft de dimensie van oppervlakte.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... gasdruk22
- We vinden de uitdrukking voor de gasdruk
uit de ideale gaswet,
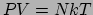 , met
, met 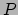 de gasdruk,
de gasdruk, 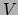 het volume,
het volume, 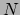 het aantal moleculen,
het aantal moleculen, 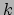 de constante van Boltzmann en
de constante van Boltzmann en 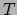 de temperatuur. Omdat
de deeltjesdichtheid,
de temperatuur. Omdat
de deeltjesdichtheid,
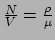 , met
, met 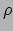 de massadichtheid,
de massadichtheid,
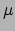 het moleculaire massa (
het moleculaire massa (
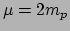 voor waterstofmoleculen, H
voor waterstofmoleculen, H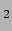 ) en
) en 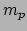 de massa van het proton, kunnen we de gasdruk ook schrijven als
de massa van het proton, kunnen we de gasdruk ook schrijven als
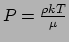 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... is23
- Voor massieve sterren met hogere temperatuur kan
stralingsdruk wel een belangrijke rol spelen.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... massa24
- Subrahmanyan Chandrasekhar (1910 - 1995)
heeft deze limiet afgeleid, die bepaalt of een instortende ster een
witte dwerg wordt of een exotischer object: neutronenster, quarkster
of zwart gat.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... elektronvangst25
- Elektronvangst
is de reactie
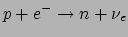 . Hierdoor worden protonen omgezet
in neutronen, terwijl de ster neutrino's uitzendt.
. Hierdoor worden protonen omgezet
in neutronen, terwijl de ster neutrino's uitzendt.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
uitrekenen26
- G. Baym en C. Pethick, Ann. Rev. Nucl. Sci. 25,
27 (1975); S. Tsuruta, Comm. Astrophys. 11, 151 (1986).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
berekening27
- M.A. Ruderman, Sci. Amer. 224, 24
(februari 1971).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
Gold28
- T. Gold, Nature 218, 731 (1968).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... flavors29
- In de natuur komen
er drie soorten neutrino's voor: elektron neutrino
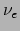 , muon neutrino
, muon neutrino
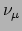 en tau neutrino
en tau neutrino 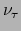 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... stromen30
- In de zwakke wisselwerking worden
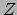 bosonen of
bosonen of 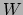 bosonen uitgewisseld. Omdat het
bosonen uitgewisseld. Omdat het 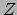 boson ongeladen
is, spreekt men van neutrale stromen. De
boson ongeladen
is, spreekt men van neutrale stromen. De 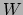 bosonen zijn geladen.
bosonen zijn geladen.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... Fermi31
- E. Fermi,
Phys. Rev. 75, 12 (1949).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...puntgebeurtenis32
- In
het Engels spreken van een event.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
transformatie33
- Voor tensorrekening is basiskennis van transformatietheorie
onontbeerlijk. Dit voorbeeld is een eerste kennismaking.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... transformatie34
- De transformaties
die een rol spelen in de ART zijn over het algemeen niet lineair.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... kromming35
- Andere voorbeelden zijn de
Hilbertruimte met complexe golffuncties van de quantummechanica,
of de Minkowskiruimte van de
speciale relativiteitstheorie.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... basis36
- Er worden vaak andere symbolen
gebruikt voor de basisvectoren, zoals
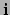 ,
, 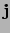 en
en 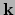 . Ook is het
mogelijk om
. Ook is het
mogelijk om 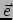 te zien als een object met hogere rang, bijvoorbeeld een
vector van vectoren. Dat is niet fout, maar in ons geval ook niet nuttig.
te zien als een object met hogere rang, bijvoorbeeld een
vector van vectoren. Dat is niet fout, maar in ons geval ook niet nuttig.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... beschreven37
- We
stappen dus af van het begrip vrije vector. In de algemene relativiteitstheorie
kunnen we een vector niet eenvoudig vrij verplaatsen!
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... functionaal38
- Terwijl
een functie een getal als argument neemt en een getal als resultaat oplevert,
neemt een functionaal een functie als argument en levert een getal als resultaat.
Een voorbeeld is de totale massa die hoort bij een dichtheidsverdeling,
waarbij
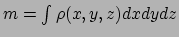 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... functionaal39
- Net zoals
we vectoren aangeven door een pijltje (
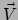 ) boven het symbool te plaatsen, geven
een lineaire functionaal aan door er een tilde (
) boven het symbool te plaatsen, geven
een lineaire functionaal aan door er een tilde (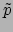 ) boven te plaatsen.
) boven te plaatsen.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... getal40
- Je kunt de 1-vorm zien als
een apparaat met een sleuf. Als in deze sleuf een vector geplaatst wordt,
dan rolt er een getal uit het apparaat.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... basis41
- Dit is
niet de enig mogelijke basis voor 1-vormen. Men kan eenvoudig
laten zien dat andere basis 1-vormen voldoen aan
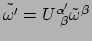 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... superscipten42
- Door de indices als superscripten te
plaatsen kunnen we weer gebruik maken van de elegante en compacte indexnotatie.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... tensoren43
- Vergelijk
dit eens met wat we gedaan hebben in vergelijking (130).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... argumenten44
- Men kan een
dergelijke tensor opvatten als een apparaat met
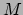 gaten waar
men 1-vormen en
gaten waar
men 1-vormen en 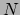 gaten waar men
vectoren in kan stoppen. Nadat men die
gaten waar men
vectoren in kan stoppen. Nadat men die 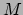 1-vormen en
1-vormen en 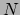 vectoren erin gestopt heeft,
rolt er een reëel getal uit het apparaat. De uitkomst is lineair
in elk van de vectoren en 1-vormen die als input gebruikt zijn.
vectoren erin gestopt heeft,
rolt er een reëel getal uit het apparaat. De uitkomst is lineair
in elk van de vectoren en 1-vormen die als input gebruikt zijn.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... perfect45
- Later
zullen we zien dat er wel degelijk een afwijking bekend was van de planeetbanen
zoals beschreven door newtoniaanse wetten, te weten de perihelium verschuiving
van Mercurius. Het verklaren van deze afwijking was een van de eerste
experimentele verificaties van Einstein's theorie van de zwaartekracht: de algemene
relativiteitstheorie. We komen hier in latere hoofdstukken op terug.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
geheel46
- Ook hier geldt een kleine opmerking: er waren enkele
onduidelijkheiden (zoals de Gibbs correctie factor) die later verklaard zijn
door de quantummechanica.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ....47
- De keuze voor de
letter
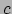 komt van het Griekse woord voor snelheid, celeritas.
komt van het Griekse woord voor snelheid, celeritas.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... algemeen48
- Er zijn
uitzonderingen op deze regel: er bestaan ook grootheden die hetzelfde zijn voor
alle waarnemers. Een ervan is al genoemd: de lichtsnelheid
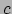 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
vormen49
- Merk op dat met de definitie
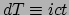 , we het lijnelement
kunnen schrijven als
, we het lijnelement
kunnen schrijven als
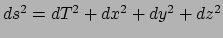 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... optreedt50
- De correcte plaatsing van de lorentzfactor
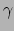 kan soms verwarrend zijn: welke waarnemer meet nu een langere tijdsduur?
De vuistregel is altijd, dat de waarnemer die in rust is ten opzichte van de twee gebeurtenissen,
de kortste tijdsduur meet tussen de twee gebeurtenissen. Dit betekent hier dat
kan soms verwarrend zijn: welke waarnemer meet nu een langere tijdsduur?
De vuistregel is altijd, dat de waarnemer die in rust is ten opzichte van de twee gebeurtenissen,
de kortste tijdsduur meet tussen de twee gebeurtenissen. Dit betekent hier dat
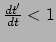 ,
wat aangeeft hoe de factor
,
wat aangeeft hoe de factor 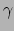 geplaatst dient te worden.
geplaatst dient te worden.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... beschrijven51
- Deze alternatieve maat voor de snelheid wordt in
sommige takken van de fysica meer gebruikt dan de snelheid
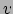 ; hij heeft als naam
de rapidity. De reden voor deze voorkeur is dat
de snelheid
; hij heeft als naam
de rapidity. De reden voor deze voorkeur is dat
de snelheid 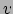 tussen waarnemers nooit groter kan zijn dan de lichtsnelheid, terwijl
de rapidity wel degelijk
tussen waarnemers nooit groter kan zijn dan de lichtsnelheid, terwijl
de rapidity wel degelijk 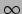 groot kan worden. Dit heeft soms rekenkundige voordelen.
groot kan worden. Dit heeft soms rekenkundige voordelen.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... gebruikt52
- Deze rekenregels zijn eenvoudig
te bewijzen met behulp van de definities:
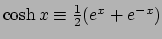 ,
,
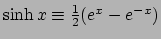 ,
,
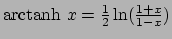
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
licht53
- Dit geldt in de conventionele leer van de natuurkunde. Er zijn wel
degelijk exotische theorieën waarin deeltjes bestaan die sneller gaan dan het licht
(de zogenaamde tachyonen); echter, theorieën met tachyonen hebben doorgaans
de eigenschap instabiele materie te voorspellen. Zulke deeltjes zullen daarom niet
worden beschouwd.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
ruimte54
- Tijd wordt door Aristoteles niet voorgesteld als een kopie
van de reëele lijn
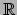 , want
, want
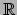 bevat het voorkeurselement
0. Er is echter geen sprake van een voorkeur voor een oorsprong in de
beschrijving van dynamische objecten.
bevat het voorkeurselement
0. Er is echter geen sprake van een voorkeur voor een oorsprong in de
beschrijving van dynamische objecten.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
vorm55
- Dit is een generalisatie van vergelijking (28).
Het bewijs van deze stelling
gaat analoog aan dat van vergelijking (28).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
betekenis56
- Denk bijvoorbeeld aan de relatie tussen een kracht
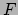 in de
in de 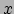 -richting en de potentiële energie
-richting en de potentiële energie 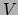 :
:
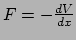 ,
oftewel een meetbare grootheid is uitgedrukt als een verschil in energie.
,
oftewel een meetbare grootheid is uitgedrukt als een verschil in energie.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... geheel57
- Er is een subtiel maar belangrijk verschil: deze
uitdrukking geeft niet de energie van een deeltje, maar het kwadraat van
de energie; er moet dus nog een wortel worden genomen! Nu heeft een kwadratische
vergelijking altijd twee oplossingen: een met een plusteken, en een met een minteken.
De laatste oplossing duidt op deeltjes met een negatieve energie, iets wat
vergelijking (214) nog
niet deed! Het correct interpreteren van deze nieuwe oplossingen leidde Paul Dirac
tot het voorspellen van het bestaan van antimaterie.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... nul58
- Een omgekeerde conclusie kan ook worden getrokken uit
vergelijking (214):
als een deeltje een massa gelijk aan nul zou hebben maar niet zou bewegen met
de lichtsnelheid, zou alleen de teller nul zijn, en daarmee de hele uitdrukking
voor de energie. Deeltjes zonder energie bestaan niet (alles heeft energie),
en dus volgt nu ook dat als een deeltje geen massa heeft, het noodzakelijkerwijs
met de lichtsnelheid moet bewegen.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
fotonen59
- Er zijn nog meer massaloze deeltjes die met de lichtsnelheid bewegen:
gluonen en gravitonen. Voor het gemak spreken we alleen over de fotonen,
maar impliciet bedoelen we hier alle massaloze deeltjes mee.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... nul60
- Stel dat voor twee lineaire
vergelijkingen geldt
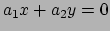 en
en
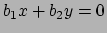 .
Als we
.
Als we 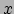 en
en 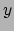 elimineren vinden we de uitdrukking
elimineren vinden we de uitdrukking
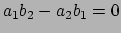 . In dat geval
is het systeem singulier. In de limiet
van gelijke punten
. In dat geval
is het systeem singulier. In de limiet
van gelijke punten
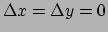 dient te gelden dat
dient te gelden dat
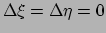 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...eq:vvx).61
- Het is van belang expliciet te
controleren dat
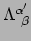 en
en
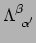 elkaars inverse zijn. Dus
elkaars inverse zijn. Dus
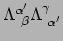 is
is
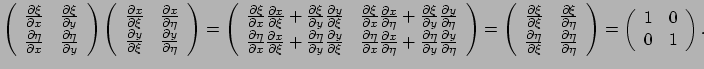 |
(244) |
Merk op dat een en ander volgt uit de definitie van partiële afgeleide
en dat 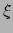 en
en 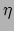 onafhankelijke variabelen zijn en dus geldt
onafhankelijke variabelen zijn en dus geldt
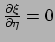 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... worden62
- Wellicht
dat een andere kijk op deze zaak verhelderend is: we gaan weer uit van
vergelijking (251) en omdat
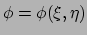 verwacht
je voor de afgeleide van
verwacht
je voor de afgeleide van 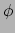 langs de raakvector
langs de raakvector 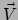 van de curve
van de curve
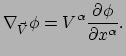 |
(246) |
Het symbool
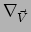 betekent de waarde van de richtingsafgeleide
van een scalairveld in de richting gegeven door vector
betekent de waarde van de richtingsafgeleide
van een scalairveld in de richting gegeven door vector 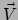 . Dus geldt
. Dus geldt
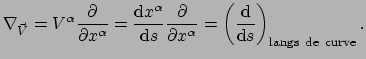 |
(247) |
Merk op dat we nu de volgende situatie hebben,
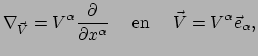 |
(248) |
en zien dat beide uitdrukkingen dezelfde expansiecoëfficiënten 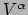 hebben. De eerste vergelijking is voor een richtingsafgeleide en de tweede
beschrijft een vector. Er is dus een isomorfisme tussen vectoren en richtingsafgeleiden.
We mogen derhalve schrijven
hebben. De eerste vergelijking is voor een richtingsafgeleide en de tweede
beschrijft een vector. Er is dus een isomorfisme tussen vectoren en richtingsafgeleiden.
We mogen derhalve schrijven
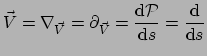 |
(249) |
en voor de basisvectoren
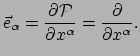 |
(250) |
Voor een wiskundige is de tangentruimte de ruimte opgespannen door de richtingsafgeleiden
op punt
 . Deze richtingsafgeleiden hebben dus hun eigen ruimte.
. Deze richtingsafgeleiden hebben dus hun eigen ruimte.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... uitdrukking63
- Verwar
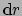 en
en
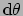 niet met de basis 1-vormen
niet met de basis 1-vormen
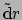 en
en
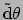 . Het zijn de
componenten van
. Het zijn de
componenten van
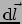 in poolcoördinaten en de `d' betekent `oneindig kleine
in poolcoördinaten en de `d' betekent `oneindig kleine 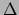 '.
'.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... genoemd64
- Ter verheldering bekijken
we de covariante afgeleide
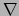 weer als een geometrisch object, dit wil zeggen als een
apparaat met drie sleuven. Op elk punt
weer als een geometrisch object, dit wil zeggen als een
apparaat met drie sleuven. Op elk punt
 van ruimtetijd bevindt zich
een dergelijk apparaat. De interpretatie is dat
van ruimtetijd bevindt zich
een dergelijk apparaat. De interpretatie is dat
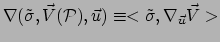 . We stoppen een willekeurige 1-vorm
. We stoppen een willekeurige 1-vorm
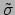 die in de tangentruimte bestaat op punt
die in de tangentruimte bestaat op punt
 in de eerste sleuf. In de
tweede sleuf stoppen we een vectorveld
in de eerste sleuf. In de
tweede sleuf stoppen we een vectorveld
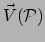 dat in de omgeving van
dat in de omgeving van
 gedefinieerd is. Tenslotte stoppen we in de derde sleuf een vector
gedefinieerd is. Tenslotte stoppen we in de derde sleuf een vector
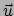 die zich in de tangentruimte van punt
die zich in de tangentruimte van punt
 bevindt. Uit de
machine rolt nu een getal dat het inproduct is van de covariante afgeleide
bevindt. Uit de
machine rolt nu een getal dat het inproduct is van de covariante afgeleide
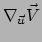 van het vectorveld
van het vectorveld 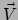 in de richting
in de richting 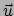 met de 1-vorm
met de 1-vorm
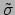 . Je kunt
. Je kunt
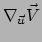 zien als de
mate van verandering van
zien als de
mate van verandering van 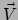 langs de vector
langs de vector 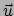 . Een alternatieve
manier om ernaar te kijken is om de eerste sleuf leeg te laten. We krijgen dan een
nieuw vectorveld
. Een alternatieve
manier om ernaar te kijken is om de eerste sleuf leeg te laten. We krijgen dan een
nieuw vectorveld
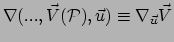 uit het oude vectorveld
uit het oude vectorveld 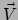 . We noemen dat de covariante afgeleide van het
vectorveld
. We noemen dat de covariante afgeleide van het
vectorveld 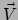 langs de vector
langs de vector 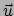 . Tenslotte is er een derde manier om
de zaak te bekijken: we laten zowel de eerste als de derde sleuf leeg. We krijgen
nu een
. Tenslotte is er een derde manier om
de zaak te bekijken: we laten zowel de eerste als de derde sleuf leeg. We krijgen
nu een
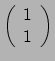 tensorveld
tensorveld
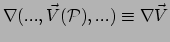 uit het
originele vectorveld
uit het
originele vectorveld 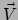 . Dit noemen we de covariante afgeleide of de
gradiënt van het vectorveld
. Dit noemen we de covariante afgeleide of de
gradiënt van het vectorveld 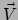 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... nemen65
- We kunnen altijd een lokaal lorentzframe
construeren, dat voldoende vlak is voor wat wij willen. In dat systeem
zijn de basisvectoren constant en hun afgeleiden nul in punt
 .
Dit is een definitie voor de covariante afgeleide. Deze definitie
leidt er onmiddellijk toe dat de christoffelsymbolen gelijk zijn aan
nul en dat in het LLF geldt
.
Dit is een definitie voor de covariante afgeleide. Deze definitie
leidt er onmiddellijk toe dat de christoffelsymbolen gelijk zijn aan
nul en dat in het LLF geldt
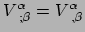 op punt
op punt
 . Dit is natuurlijk waar voor elke tensor en ook
voor de metriek,
. Dit is natuurlijk waar voor elke tensor en ook
voor de metriek,
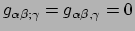 op punt
op punt
 . Omdat de vergelijking
. Omdat de vergelijking
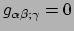 een tensorvergelijking is, is hij geldig in elke basis. Gegeven dat
een tensorvergelijking is, is hij geldig in elke basis. Gegeven dat
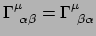 , vinden we
weer dat voor elke metriek dient te gelden
, vinden we
weer dat voor elke metriek dient te gelden
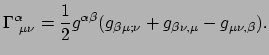 |
(318) |
Dus terwijl
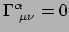 op
op
 in het LLF, geldt dat niet
voor de afgeleiden ervan, want die bevatten
in het LLF, geldt dat niet
voor de afgeleiden ervan, want die bevatten
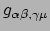 .
Dus de christoffelsymbolen zijn dan wel nul op punt
.
Dus de christoffelsymbolen zijn dan wel nul op punt
 als we
een LLF kiezen, maar verschillen in het algemeen van nul in de omgeving van dit punt.
Het verschil tussen een gekromde en een vlakke variëteit manifesteert
zich dus in de afgeleiden van de christoffelsymbolen.
als we
een LLF kiezen, maar verschillen in het algemeen van nul in de omgeving van dit punt.
Het verschil tussen een gekromde en een vlakke variëteit manifesteert
zich dus in de afgeleiden van de christoffelsymbolen.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... coëfficiënten66
- Deze
staan ook bekend als de christoffelsymbolen.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... genoemd)67
- In een coördinatenbasis worden de basisvectoren gegeven
door de partiële afgeleiden,
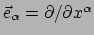 , en omdat partiële
afgeleiden commuteren, moet gelden
, en omdat partiële
afgeleiden commuteren, moet gelden
![$ [\vec e_\alpha , \vec e_\beta ] = 0$](img1482.png) .
In een niet-coördinatenbasis geldt
.
In een niet-coördinatenbasis geldt
![$ [\vec e_\mu , \vec e_\nu ] = C_{\mu \nu}^\alpha \vec e_\alpha$](img1483.png) , met
, met
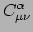 de zogenaamde commutatie coëfficiënten. Een
coördinatenbasis is handig voor het doen van berekeningen, terwijl
een niet-coördinatenbasis nuttig kan zijn voor de interpretatie van
gegevens.
de zogenaamde commutatie coëfficiënten. Een
coördinatenbasis is handig voor het doen van berekeningen, terwijl
een niet-coördinatenbasis nuttig kan zijn voor de interpretatie van
gegevens.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... bevat68
- Behalve intrinsieke kromming kan een
variëteit ook een extrinsieke kromming hebben. Neem bijvoorbeeld
een blad papier dat geen intrinsieke kromming heeft, en rol het op tot
een cilinder. Deze cilinder heeft extrensieke kromming en die beschrijft
de inbedding van het vlakke blad papier in de 3D ruimte. De ART zegt
niets over de hogere ruimten waarin ruimtetijd kan zijn ingebed. De ART
geeft een beschrijving van kromming binnen de variëteit zelf en dat
is de intrinsieke kromming van ruimtetijd.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... waarnemer69
- We
gaan er voor het gemak vanuit dat wij als waarnemer niet van invloed
zijn op het proces. Het belangrijkste is dat we aannemen dat we geen kracht uitoefenen
en geen kromming veroorzaken.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... gebruikt70
- In het LLF komt
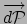 overeen met
overeen met
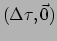 , waarbij
, waarbij
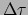 de eigentijd is, gemeten
met een ideale klok. Er geldt dan dat
de eigentijd is, gemeten
met een ideale klok. Er geldt dan dat
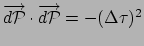 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... is71
- In dat geval geldt
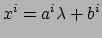 en wordt bijvoorbeeld
en wordt bijvoorbeeld
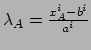 . Dan geldt
. Dan geldt
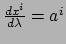 waardoor de afgeleide niet meer van
waardoor de afgeleide niet meer van 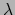 afhangt en buiten de integraal gehaald kan worden. Verder schrijven we
afhangt en buiten de integraal gehaald kan worden. Verder schrijven we
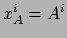 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
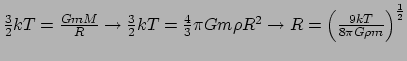 .
Een exacte berekening die de geluidssnelheid in de gaswolk in rekening brengt,
levert vergelijking (38).
.
Een exacte berekening die de geluidssnelheid in de gaswolk in rekening brengt,
levert vergelijking (38).
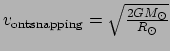 .
De kinetische energie van een atoom als het de zon bereikt is dus
.
De kinetische energie van een atoom als het de zon bereikt is dus
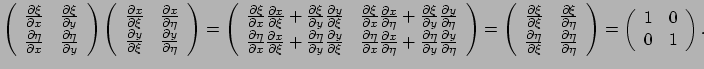
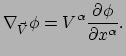
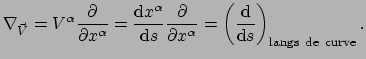
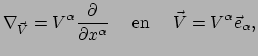
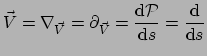
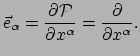
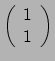 tensorveld
tensorveld
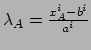 . Dan geldt
. Dan geldt