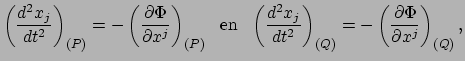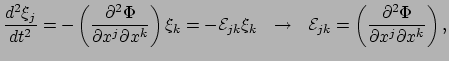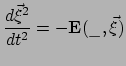Next: De einsteinvergelijkingen
Up: De algemene relativiteitstheorie
Previous: Kromming en de riemanntensor
Contents
We proberen een maat te vinden voor de kromming van ruimtetijd. Hiertoe
laten we een testdeeltje vrij vallen. Wij besluiten als waarnemer69 om met
dit deeltje mee te vallen (LLF) en zien dat het deeltje langs een rechte
lijn in ruimtetijd beweegt (enkel in de tijdrichting).
Er is niets in de beweging van een enkel deeltje dat
kromming verraadt. Met name in het vrij vallende coördinatenstelsel blijft
het deeltje in rust. Eén deeltje is onvoldoende om de effecten van
kromming te ontdekken.
Vervolgens laten we twee deeltjes vallen.
We gaan de getijdenkracht op aarde bekijken vanuit het perspectief
van waarnemers die vrijvallen (LLF) samen met de deeltjes. Dergelijke waarnemers vallen
in een rechte lijn naar het centrum van de aarde. Fig. 49
geeft de situatie voor twee vrij vallende deeltjes  en
en 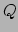 , en we zien dat beide
deeltjes paden volgen die leiden naar het centrum van de aarde.
, en we zien dat beide
deeltjes paden volgen die leiden naar het centrum van de aarde.
Figuur 49:
Links: twee vrij vallende deeltjes bewegen op initieel parallel paden
naar het centrum van de aarde. Daar ligt het snijpunt van beide lijnen;
rechts: lijnen op het aardoppervlak die initieel parallel zijn bij
de evenaar, snijden elkaar bij de noordpool.
|
|
Vanuit het perspectief van een waarnemer die in vrije val is met
deze deeltjes, zien we dat de deeltjes naar elkaar toe bewegen. Dit wordt
veroorzaakt door de differentiële gravitatieversnelling op de
deeltjes en we noemen dit getijdenkrachten. Volgens
Newton kruisen de paden ten gevolge van gravitatie, terwijl dit volgens
Einstein gebeurt omdat ruimtetijd gekromd is. Wat Newton gravitatie noemt,
wordt door Einstein kromming van ruimtetijd genoemd. Gravitatie is een eigenschap van
de kromming van ruimtetijd.
Figuur 50:
De banen van twee vrijvallende deeltjes in een gravitatieveld 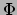 .
De drievector
.
De drievector 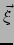 meet de afstand tussen de twee deeltjes en is een
functie van de tijd.
meet de afstand tussen de twee deeltjes en is een
functie van de tijd.
|
|
We willen nu een wiskundige beschrijving geven van dit proces, die in overeenstemming
is met de wetten van Newton (zie ook hoofdstuk 2.6).
Hiertoe beschouwen we Fig. 50.
De newtoniaanse bewegingsvergelijkingen voor deeltjes 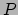 en
en  zijn
zijn
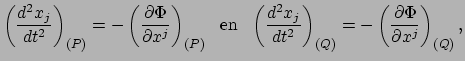 |
(342) |
met 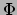 de gravitationele potentiaal. We definiëren
de gravitationele potentiaal. We definiëren 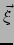 als de afstand
tussen beide deeltjes. Voor parallelle banen zou gelden
als de afstand
tussen beide deeltjes. Voor parallelle banen zou gelden
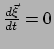 .
Met
.
Met
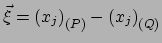 vinden we
via een Taylorexpansie
vinden we
via een Taylorexpansie
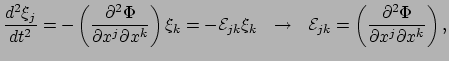 |
(343) |
met 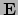 de gravitationele getijdentensor. Merk op dat de metriek voor de 3D euclidische
ruimte gegeven wordt door
de gravitationele getijdentensor. Merk op dat de metriek voor de 3D euclidische
ruimte gegeven wordt door
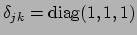 en dat er dus geen verschil
is tussen boven- en benedenindices. Vergelijking (349) wordt de vergelijking
van newtoniaanse geodetische deviatie genoemd.
en dat er dus geen verschil
is tussen boven- en benedenindices. Vergelijking (349) wordt de vergelijking
van newtoniaanse geodetische deviatie genoemd.
Volgens Newton bewegen de deeltjes naar elkaar toe en schrijven we
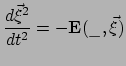 |
(344) |
in abstracte notatie. Het is interessant dat de veldvergelijking van
newtoniaanse gravitatie, vergelijking (18),
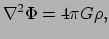 |
(345) |
kan worden uitgedrukt in termen van tweede afgeleiden van 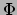 , die de
getijden versnellingen in vergelijking (349) beschrijven. Er is
een analoge connectie in de ART.
, die de
getijden versnellingen in vergelijking (349) beschrijven. Er is
een analoge connectie in de ART.




Next: De einsteinvergelijkingen
Up: De algemene relativiteitstheorie
Previous: Kromming en de riemanntensor
Contents
Jo van den Brand
2009-01-31
![\includegraphics[width=8cm]{Figures/gd.eps}](img1497.png)
![\includegraphics[width=9cm]{Figures/gd1.eps}](img1498.png)