



Next: Pseudo-riemannse variëteit
Up: gw
Previous: Berekenen van de christoffelsymbolen
Contents
De algemene relativiteitstheorie
Ruimtetijd is een variëteit die
continu en differentieerbaar is. Dat betekent dat we bijvoorbeeld
een scalairveld kunnen definiëren, waarvan dan op elk punt
de afgeleiden bepaald kunnen worden.
Het betekent ook dat we 1-vormen en vectoren kunnen definiëren
en op een bepaald punt
 van de variëteit zijn
de elementen van de verzameling
van de variëteit zijn
de elementen van de verzameling
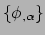 de componenten van de 1-vorm. Elke verzameling van de vorm
de componenten van de 1-vorm. Elke verzameling van de vorm
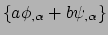 , met
, met 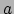 en
en 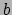 functies,
is ook een 1-vorm. Elke curve (met parameter
functies,
is ook een 1-vorm. Elke curve (met parameter 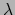 ) heeft
een raakvector
) heeft
een raakvector 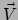 en dat is een lineaire functie die een
1-vorm
en dat is een lineaire functie die een
1-vorm
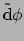 als argument neemt en de afgeleide
van
als argument neemt en de afgeleide
van 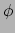 langs de curve produceert,
langs de curve produceert,
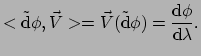 |
(300) |
Elke lineaire combinatie van vectoren is ook weer een vector.
Gebruikmakend van de op deze manier gedefinieerde vectoren en
1-vormen, kunnen we een hele verzameling tensoren van het type
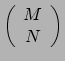 opbouwen. Omdat we nog geen
opbouwen. Omdat we nog geen
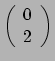 tensor gekozen hebben om dienst te doen als metriek, is er nog geen
correspondentie tussen 1-vormen en vectoren. We zeggen dat de
verzameling van alle tensoren deel uitmaakt van de differentiaalstructuur
van de variëteit.
tensor gekozen hebben om dienst te doen als metriek, is er nog geen
correspondentie tussen 1-vormen en vectoren. We zeggen dat de
verzameling van alle tensoren deel uitmaakt van de differentiaalstructuur
van de variëteit.
Voordat we verder gaan, vatten we de regels van tensoralgebra
nog eens samen.
- Een tensorveld definieert een tensor op elk punt
 van de variëteit.
van de variëteit.
- Vectoren en 1-vormen zijn lineaire operatoren op elkaar en
produceren reële getallen. Lineair betekent dat
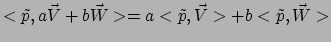 , en
, en
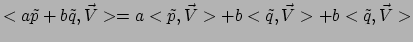 , met
, met 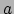 en
en 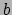 willekeurige scalaire velden.
willekeurige scalaire velden.
- Tensoren zijn op dezelfde manier lineaire operatoren op
1-vormen en vectoren, en produceren reële getallen.
- Als twee tensoren van hetzelfde type dezelfde componenten
hebben op een gegeven basis, dan hebben ze dezelfde componenten
op alle bases en zeggen we dat ze identiek zijn. In het bijzonder,
als de componenten van een tensor voor een bepaalde basis nul
zijn, dan is de tensor gelijk aan nul.
- Er is een aantal toegestane operaties met componenten van
tensorvelden. Dergelijke operaties produceren nieuwe tensoren.
- Vermenigvuldigen met een scalairveld produceert een tensor van
hetzelfde type.
- Optellen van de componenten van twee tensoren van
hetzelfde type geeft de componenten van een nieuwe tensor
van hetzelfde type. Enkel tensoren van hetzelfde type kunnen
gelijk zijn aan elkaar.
- Vermenigvuldigen van componenten van twee tensoren
van willekeurig type geeft componenten van een nieuwe tensor
die de som is van de typen, het tensorproduct van de twee tensoren.
- De covariante afgeleide van de componenten van een
tensor van type
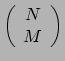 geeft de componenten van een tensor van het type
geeft de componenten van een tensor van het type
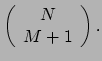
- Contractie van een paar indices van de componenten van
een tensor van het type
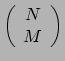 produceert componenten van een tensor van het type
produceert componenten van een tensor van het type
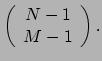 Contractie is enkel gedefinieerd tussen boven en beneden indices.
Contractie is enkel gedefinieerd tussen boven en beneden indices.
- Als een vergelijking gevormd wordt door het combineren
van componenten van tensoren, terwijl we enkel gebruik maken
van toegestane tensorbewerkingen, en als deze vergelijking
geldig is in één basis, dan is hij geldig in alle bases.
Subsections




Next: Pseudo-riemannse variëteit
Up: gw
Previous: Berekenen van de christoffelsymbolen
Contents
Jo van den Brand
2009-01-31
![]() van de variëteit zijn
de elementen van de verzameling
van de variëteit zijn
de elementen van de verzameling
![]() de componenten van de 1-vorm. Elke verzameling van de vorm
de componenten van de 1-vorm. Elke verzameling van de vorm
![]() , met
, met ![]() en
en ![]() functies,
is ook een 1-vorm. Elke curve (met parameter
functies,
is ook een 1-vorm. Elke curve (met parameter ![]() ) heeft
een raakvector
) heeft
een raakvector ![]() en dat is een lineaire functie die een
1-vorm
en dat is een lineaire functie die een
1-vorm
![]() als argument neemt en de afgeleide
van
als argument neemt en de afgeleide
van ![]() langs de curve produceert,
langs de curve produceert,
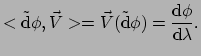
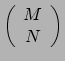 opbouwen. Omdat we nog geen
opbouwen. Omdat we nog geen
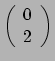 tensor gekozen hebben om dienst te doen als metriek, is er nog geen
correspondentie tussen 1-vormen en vectoren. We zeggen dat de
verzameling van alle tensoren deel uitmaakt van de differentiaalstructuur
van de variëteit.
tensor gekozen hebben om dienst te doen als metriek, is er nog geen
correspondentie tussen 1-vormen en vectoren. We zeggen dat de
verzameling van alle tensoren deel uitmaakt van de differentiaalstructuur
van de variëteit.
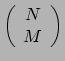 geeft de componenten van een tensor van het type
geeft de componenten van een tensor van het type
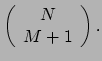
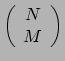 produceert componenten van een tensor van het type
produceert componenten van een tensor van het type
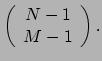 Contractie is enkel gedefinieerd tussen boven en beneden indices.
Contractie is enkel gedefinieerd tussen boven en beneden indices.