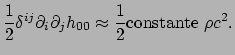Next: De kosmologische constante
Up: De algemene relativiteitstheorie
Previous: Zwakke gravitatievelden en de
Contents
De zwakke-veld limiet van de einsteinvergelijkingen
De einsteinvergelijkingen (373) stellen dat de einsteintensor evenredig
is aan de energie-impuls tensor,
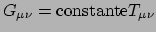 .
We willen de evenredigheidsfactor bepalen, door de zwakke-veld limiet
te nemen. Hiertoe hoeven we enkel de
.
We willen de evenredigheidsfactor bepalen, door de zwakke-veld limiet
te nemen. Hiertoe hoeven we enkel de 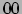 -component te beschouwen. We vinden dan
-component te beschouwen. We vinden dan
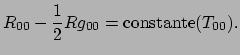 |
(380) |
In de zwakke-veld limiet is ruimtetijd slechts weinig gekromd en bestaan
er coördinaten waarvoor
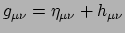 met
met
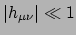 , terwijl de metriek stationair is.
Er geldt dus
, terwijl de metriek stationair is.
Er geldt dus
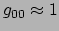 . Verder kunnen we de definitie (340)
van de krommingstensor gebruiken om
. Verder kunnen we de definitie (340)
van de krommingstensor gebruiken om 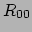 te vinden. Er geldt
te vinden. Er geldt
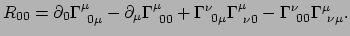 |
(381) |
In ons coördinatenstelsel zijn de
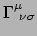 klein, zodat
we de laatste twee terming in eerste-orde in
klein, zodat
we de laatste twee terming in eerste-orde in
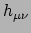 kunnen
verwaarlozen. Ook is de metriek stationair in ons coördinatenstelsel,
en vinden we
kunnen
verwaarlozen. Ook is de metriek stationair in ons coördinatenstelsel,
en vinden we
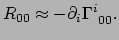 |
(382) |
In onze discussie van de newtoniaanse limiet, hebben we in vergelijking
(380) gevonden dat
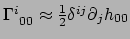 in
eerste-orde in
in
eerste-orde in
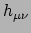 . Dus geldt
. Dus geldt
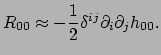 |
(383) |
We kunnen nu onze benaderingen voor 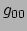 en
en 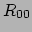 substitueren
in vergelijking (386) en vinden in de zwakke-veld limiet
substitueren
in vergelijking (386) en vinden in de zwakke-veld limiet
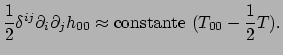 |
(384) |
We hebben hierbij gebruikt dat
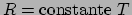 met
met
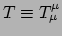 ,
door vergelijking (373) met gemengde componenten te
schrijven,
,
door vergelijking (373) met gemengde componenten te
schrijven,
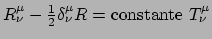 ,
en deze te contraheren door
,
en deze te contraheren door 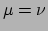 te stellen (merk op dat
te stellen (merk op dat
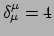 ).
).
Om voortgang te kunnen maken, moeten we nu iets aannemen over de soort materie
die het zwakke gravitationele veld produceert. We nemen hiervoor een perfecte
vloeistof. Voor de meeste klassieke materieverdelingen geldt
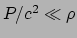 en we kunnen de energie-impuls tensor voor stof nemen. Er geldt
en we kunnen de energie-impuls tensor voor stof nemen. Er geldt
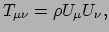 |
(385) |
en hiermee vinden we
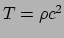 . Verder nemen we aan dat de deeltjes
die de vloeistof vormen, snelheden
. Verder nemen we aan dat de deeltjes
die de vloeistof vormen, snelheden 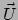 hebben die in ons coördinatenstelsel
klein zijn ten opzichte van
hebben die in ons coördinatenstelsel
klein zijn ten opzichte van 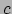 . We doen de aanname
. We doen de aanname
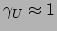 en dus
en dus
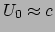 . Vergelijking (390) reduceert dan tot
. Vergelijking (390) reduceert dan tot
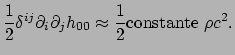 |
(386) |
We merken op dat
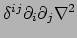 . Verder hebben
we met vergelijking (383)
. Verder hebben
we met vergelijking (383)
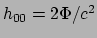 , met
, met 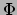 de gravitatiepotentiaal. Als we de evenredigheidsconstante nu kiezen
als
de gravitatiepotentiaal. Als we de evenredigheidsconstante nu kiezen
als
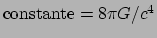 , dan vinden we de poissonvergelijking
voor newtoniaanse gravitatie (zie ook vergelijking (18))
, dan vinden we de poissonvergelijking
voor newtoniaanse gravitatie (zie ook vergelijking (18))
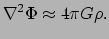 |
(387) |
Deze identificatie verifieert onze aanname dat de evenredigheidsfactor
tussen de einsteintensor en de energie-impuls tensor gelijk is aan
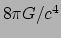 .
.




Next: De kosmologische constante
Up: De algemene relativiteitstheorie
Previous: Zwakke gravitatievelden en de
Contents
Jo van den Brand
2009-01-31
![]() .
We willen de evenredigheidsfactor bepalen, door de zwakke-veld limiet
te nemen. Hiertoe hoeven we enkel de
.
We willen de evenredigheidsfactor bepalen, door de zwakke-veld limiet
te nemen. Hiertoe hoeven we enkel de ![]() -component te beschouwen. We vinden dan
-component te beschouwen. We vinden dan
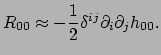
![]() en we kunnen de energie-impuls tensor voor stof nemen. Er geldt
en we kunnen de energie-impuls tensor voor stof nemen. Er geldt