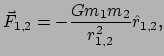 |
(12) |
We hebben reeds in vergelijking (7) gezien dat de gravitatiekracht
uitgeoefend door deeltje 1 op deeltje 2 gegeven wordt door
We beschouwen de situatie met ![]() de massa van een deeltje
en
de massa van een deeltje
en ![]() de massa van een massief object, bijvoorbeeld
de aarde. We stellen ons voor dat het deeltje in
een cirkelbaan rond de aarde beweegt. Er geldt
de massa van een massief object, bijvoorbeeld
de aarde. We stellen ons voor dat het deeltje in
een cirkelbaan rond de aarde beweegt. Er geldt ![]() en dit
betekent dat
en dit
betekent dat
![]() de versnelling van het deeltje is.
Deze versnelling is centripetaal en we vinden dan
de versnelling van het deeltje is.
Deze versnelling is centripetaal en we vinden dan
Als we een deeltje van de aarde naar het oneindige brengen, dient er arbeid
verricht te worden. Deze arbeid is gelijk (maar met een minteken) aan de potentiële
energie ![]() van het deeltje (als we immers het deeltje vanuit het oneindige op
de aarde laten vallen verkrijgt het kinetische energie en kan het weer arbeid
verrichten). De hoeveelheid potentiële energie wordt gegeven door
van het deeltje (als we immers het deeltje vanuit het oneindige op
de aarde laten vallen verkrijgt het kinetische energie en kan het weer arbeid
verrichten). De hoeveelheid potentiële energie wordt gegeven door
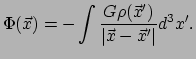 |
(16) |
| (17) |
Een object, bijvoorbeeld een satelliet met massa ![]() , dat in een willekeurige
baan met straal
, dat in een willekeurige
baan met straal ![]() rond de aarde (met massa
rond de aarde (met massa ![]() ) draait heeft
zowel kinetische energie
) draait heeft
zowel kinetische energie ![]() 11
als potentiële energie
11
als potentiële energie ![]() . De som van beide, de totale energie
. De som van beide, de totale energie ![]() ,
is een behouden grootheid en dient constant te zijn. Er geldt
,
is een behouden grootheid en dient constant te zijn. Er geldt
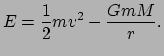 |
(19) |
De Deense sterrenkundige Olaf Roemer (1644 - 1710) gaf als eerste een goede
schatting van de lichtsnelheid (hij vond 11 minuten per astronomische eenheid
(AU)12,
terwijl de juiste waarde 8 minuten en 19 seconden is). Dit resultaat vond hij
in 1675 door de eclipse van Jupiter's eerste satelliet te bestuderen voor
verschillende posities van Jupiter relatief ten opzichte van de aarde.
De Britse natuurkundige John Mitchell (1724 - 1793) en de Franse wiskundige en
natuurkundige Pierre Laplace (1749 - 1827) combineerden de eindige lichtsnelheid
met het feit dat uit de wetten van Newton volgt dat geen object van een lichaam
kan ontsnappen als haar snelheid minder is dan
![]() .
Hieruit volgt dat ook licht niet kan ontsnappen van een lichaam waarvan
de ontsnappingssnelheid groter is dan
.
Hieruit volgt dat ook licht niet kan ontsnappen van een lichaam waarvan
de ontsnappingssnelheid groter is dan ![]() . Dus als het mogelijk is om een
lichaam met vaste massa
. Dus als het mogelijk is om een
lichaam met vaste massa ![]() kleiner te maken dan straal
kleiner te maken dan straal ![]() , met
, met
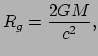 |
(21) |
Cavendisch was de eerste die in 1784 een formule afleidde voor de afbuiging
van licht ten gevolge van de gravitatie van de zon. We zullen deze afbuiging
afleiden uit het equivalentieprincipe. Beschouw licht dat de zon passeert. We
weten dat licht een rechte lijn dient te volgen in het referentiesysteem van
een vrij-vallende waarnemer. Omdat lokaal vrij-vallende waarnemers allemaal
in de zon vallen, dient het licht continu zijn baan te buigen, zodat de baan
recht lijkt voor al deze vrij-vallende locale waarnemers. We zullen de grootte
van de afbuiging afschatten met behulp van de klassieke mechanica van Newton.
![\includegraphics[width=10cm]{Figures/afbuiging.eps}](img223.png)
|
We beschouwen een enkele vrij-vallende waarnemer die initieel in rust is ten opzichte
van de zon op het punt waar het licht het dichtst bij de zon is tijdens de
passage. De afstand noemen we ![]() . De versnelling van de waarnemer naar de
zon bedraagt
. De versnelling van de waarnemer naar de
zon bedraagt
![]() . Het licht reist met snelheid
. Het licht reist met snelheid ![]() en het belangrijkste
deel van de afbuiging treedt op gedurende een tijd
en het belangrijkste
deel van de afbuiging treedt op gedurende een tijd ![]() . Gedurende deze
tijd bereikt de waarnemer een snelheid
. Gedurende deze
tijd bereikt de waarnemer een snelheid
![]() loodrecht op de richting
van het licht. Vanwege het equivalentieprincipe dient het licht een dergelijke
transversale snelheid te krijgen. De hoekafbuiging is klein en er geldt
loodrecht op de richting
van het licht. Vanwege het equivalentieprincipe dient het licht een dergelijke
transversale snelheid te krijgen. De hoekafbuiging is klein en er geldt
![]() in radialen. De totale
afbuiging dient het dubbele te zijn, omdat dezelfde afbuiging voor de inkomende
lichtstraal ook geldt voor de uitgaande lichtstraal (zie Fig. 5).
We vinden
in radialen. De totale
afbuiging dient het dubbele te zijn, omdat dezelfde afbuiging voor de inkomende
lichtstraal ook geldt voor de uitgaande lichtstraal (zie Fig. 5).
We vinden
 |
(22) |