![\includegraphics[width=10cm]{Figures/escape4.eps}](img162.png)
|
In het volgende zullen we enkele consequenties van de wetten van Newton
bestuderen. We gebruiken het equivalentieprincipe om te verklaren hoe satellieten
in hun baan blijven.
![\includegraphics[width=10cm]{Figures/escape4.eps}](img162.png)
|
De twee driehoeken zijn congruent en dus geldt
![]() (lengten van corresponderende zijden
zijn evenredig). Delen door
(lengten van corresponderende zijden
zijn evenredig). Delen door ![]() en herschikken levert
en herschikken levert
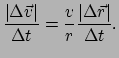 |
(10) |
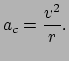 |
(11) |
In het volgende beschouwen we een satelliet die met constante snelheid in
een cirkelbaan rond het centrum van de aarde over het oppervlak beweegt.
De versnelling is nu gelijk aan ![]() m/s
m/s![]() en we vinden voor de
snelheid
en we vinden voor de
snelheid
![]() m/s
m/s![]() met
met ![]() km de waarde
km de waarde
 km/s.
De omlooptijd bedraagt
km/s.
De omlooptijd bedraagt
![]() s = 84,3 min.
s = 84,3 min.
Op grotere hoogte is de omlooptijd langer en
bedraagt bijvoorbeeld 91 minuten op 300 km hoogte waar de Space Shuttle opereert.
Astronauten in de Space Shuttle zijn gewichtsloos. Dit komt niet omdat op
300 km van het aardoppervlak het gravitatieveld van de aarde verwaarloosbaar is
(dat is eenvoudig uit te rekenen met vergelijking (7)).
Het is een perfecte demonstratie van het equivalentieprincipe: de Space Shuttle is in
vrije val rond de aarde en dat veroorzaakt dat voorwerpen in de Space
Shuttle zich gedragen alsof gravitatie afwezig is.
We willen het bovenstaande verder uitdiepen met het volgende voorbeeld.
Stel we stappen in een stilstaande lift. De sensatie van gewicht komt doordat
de vloer van de lift een kracht op ons uitoefent tegengesteld gericht aan
de gravitatiekracht van de aarde. Als we de liftkabel doorknippen, dan valt de
kracht van de vloer wel. We raken in vrije val, en dan verdwijnt de sensatie van gewicht
volledig. De vloer van de lift, niet de gravitatiekracht, is verantwoordelijk
voor ons gewicht. We kunnen dit argument omkeren: als we de lift naar boven
versnellen, zullen we ons zwaarder gaan voelen. Als we in een geblindeerde lift
zitten en we voelen ons gewichtloos, dan kunnen we niet onderscheiden of we
in vrije val zijn op aarde of in de ruimte ver weg van graviterende objecten
bevinden. Evenzo, als we wèl gewicht ervaren, weten we niet of dat komt doordat
we in een stilstaande lift op aarde staan, of dat we in de verre ruimte naar
boven worden versneld. Als gravitatie overal uniform zou zijn, kunnen we het
niet onderscheiden van versnelling. Dit is de betekenis van het woord
equivalentie in het equivalentieprincipe.