In moderne bewoording kunnen de wetten van Newton als volgt geformuleerd worden:
De eerste wet is duidelijk in overeenstemming met
de ideëen van Galileo Galileï. Het leidt
tot het relativiteitsprincipe en het feit dat beweging in verschillende richtingen
onafhankelijk behandeld kunnen worden. Ook de tweede wet is geïnspireerd door
Galileï en om dit duidelijk te maken dienen we de begrippen massa en gewicht
nader te beschouwen. Als we een voorwerp willen versnellen, dan dienen we er
een kracht op uit te oefenen. De versnelling heeft dan de waarde
![]() .
De massa
.
De massa ![]() kan gezien worden als de weerstand, inertia, tegen versnelling.
Hoe groter de massa, hoe moeilijker het is om het voorwerp in beweging te brengen.
Het gewicht van een voorwerp is de gravitatiekracht die erop werkt.
Als we de tweede wet van Newton combineren met Galileï's ontdekking dat voorwerpen
met verschillende massa's op dezelfde manier vernellen onder gravitatie, dan
betekent dit dat het gewicht van een voorwerp evenredig moet zijn met haar massa.
kan gezien worden als de weerstand, inertia, tegen versnelling.
Hoe groter de massa, hoe moeilijker het is om het voorwerp in beweging te brengen.
Het gewicht van een voorwerp is de gravitatiekracht die erop werkt.
Als we de tweede wet van Newton combineren met Galileï's ontdekking dat voorwerpen
met verschillende massa's op dezelfde manier vernellen onder gravitatie, dan
betekent dit dat het gewicht van een voorwerp evenredig moet zijn met haar massa.
Dit is als volgt in te zien: stel we tillen een zwaar voorwerp op en houden het
vast. Wat we voelen als gewicht is in werkelijkheid de sensatie van
het uitoefenen van een naar boven gerichte kracht om het voorwerp hoog te houden
tegen de werking van de zwaartekracht in. Uit de eerste wet volgt dat de totale
kracht op het voorwerp nul is en dat onze opwaartse kracht precies de zwaartekracht
op het voorwerp opheft. Het gewicht van het voorwerp is dus gelijk aan de
zwaartekracht die erop werkt. Als we het voorwerp loslaten, dan is de
zwaartekracht erop nog steeds gelijk, terwijl onze opwaartse kracht verdwenen is:
het voorwerp versnelt naar beneden, het valt. Volgens Galileï is de versnelling
echter niet afhankelijk van het gewicht. De enige manier waarop we de kracht
![]() (het gewicht) kunnen veranderen zonder de versnelling
(het gewicht) kunnen veranderen zonder de versnelling ![]() te veranderen, is
door het gewicht
te veranderen, is
door het gewicht ![]() evenredig te maken met
evenredig te maken met ![]() , dus
, dus
![]() . In dat geval geldt namelijk
. In dat geval geldt namelijk
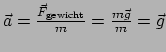 en voorwerpen vallen onafhankelijk van hun gewicht of massa, de versnelling is gelijk
voor alle voorwerpen en bedraagt 9,8 m/s
en voorwerpen vallen onafhankelijk van hun gewicht of massa, de versnelling is gelijk
voor alle voorwerpen en bedraagt 9,8 m/s![]() . We noemen de massa
. We noemen de massa ![]() die als evenredigheidsconstante optreedt in de uitdrukking voor gewicht
die als evenredigheidsconstante optreedt in de uitdrukking voor gewicht
![]() ook wel de zware massa, terwijl de massa die
optreedt in de tweede wet
ook wel de zware massa, terwijl de massa die
optreedt in de tweede wet
![]() de trage
massa. Galileï's equivalentieprincipe stelt dat zware massa en trage massa
gelijk zijn en we schrijven
de trage
massa. Galileï's equivalentieprincipe stelt dat zware massa en trage massa
gelijk zijn en we schrijven
![]() . We
kunnen Galileï's equivalentieprincipe nu als volgt formuleren: de massa
van een lichaam is evenredig met haar gewicht.
. We
kunnen Galileï's equivalentieprincipe nu als volgt formuleren: de massa
van een lichaam is evenredig met haar gewicht.
Newton liet zien dat dezelfde gravitatie die ervoor zorgt dat appels naar de
aarde vallen, er ook voor zorgt dat de maan bij de aarde blijft en dat de
aarde rond de zon beweegt. De relatief eenvoudige wiskundige uitdrukking
![]() was consistent met alle bekende meetgegevens van planeetbanen. De grootte van de kracht
tussen twee objecten met massa
was consistent met alle bekende meetgegevens van planeetbanen. De grootte van de kracht
tussen twee objecten met massa ![]() en
en ![]() gescheiden door een afstand
gescheiden door een afstand ![]() bedraagt
bedraagt