De einsteinvergelijkingen (373) zijn niet uniek. Einstein
ontdekte al snel dat hij het niet mogelijk bleek om een statisch model van
het universum te construeren op basis van de veldvergelijkingen. Deze
vergelijkingen geven altijd oplossingen die corresponderen met een
expanderend of contraherend heelal. Toen Einstein dit werk in 1916
uitvoerde was enkel onze melkweg bekend, en dat lijkt op een uniforme
verdeling van vaste sterren. Door het invoeren van de kosmologische
constante ![]() was Einstein in staat om statische modellen van
het universum te creëren (maar die blijken allemaal instabiel te zijn).
Later werd ingezien dat de melkweg slechts één van de vele
sterrenstelsels is, terwijl in 1929 Edwin Hubble de uitdijing van het
universum ontdekte. Hij bepaalde de afstanden en roodverschuivingen
van nabij gelegen sterrenstelsels en zag dat het universum expandeert;
zie Fig. 55.
De kosmologische constante bleek niet nodig te zijn. Sterker nog, als
Einstein meer vertrouwen had gehad in zijn vergelijkingen, had hij deze
expansie van het universum kunnen voorspellen. Tegenwoordig hebben we
een andere kijk op deze zaak, maar daarover later meer.
was Einstein in staat om statische modellen van
het universum te creëren (maar die blijken allemaal instabiel te zijn).
Later werd ingezien dat de melkweg slechts één van de vele
sterrenstelsels is, terwijl in 1929 Edwin Hubble de uitdijing van het
universum ontdekte. Hij bepaalde de afstanden en roodverschuivingen
van nabij gelegen sterrenstelsels en zag dat het universum expandeert;
zie Fig. 55.
De kosmologische constante bleek niet nodig te zijn. Sterker nog, als
Einstein meer vertrouwen had gehad in zijn vergelijkingen, had hij deze
expansie van het universum kunnen voorspellen. Tegenwoordig hebben we
een andere kijk op deze zaak, maar daarover later meer.
![\includegraphics[width=14cm]{Figures/hubblelaw.eps}](img1631.png)
|
Wat Einstein deed was het volgende. We weten dat
![]() en ook
en ook
![]() . Verder hebben we in vergelijkingen
(290) en (310) gezien dat ook
. Verder hebben we in vergelijkingen
(290) en (310) gezien dat ook
![]() .
We mogen elke constante veelvoud van
.
We mogen elke constante veelvoud van
![]() optellen bij
optellen bij
![]() en krijgen dan nog steeds een consistente verzameling veldvergelijkingen.
Het is gebruikelijk om de evenredigheidsconstante aan te duiden met
en krijgen dan nog steeds een consistente verzameling veldvergelijkingen.
Het is gebruikelijk om de evenredigheidsconstante aan te duiden met
![]() , en we vinden dan
, en we vinden dan
Door vergelijking (394) weer met gemengde indices te schrijven
en te contraheren vinden we
![]() .
Invullen in vergelijking (394) levert
.
Invullen in vergelijking (394) levert
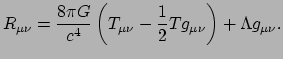 |
(389) |
| (390) |
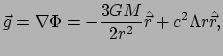 |
(391) |
Tegenwoordig hebben we een andere kijk op de kosmologische constante.
Merk op dat de energie-impuls tensor van een perfecte vloeistof gegeven
wordt door
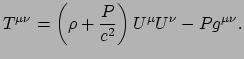 |
(392) |
| (393) |
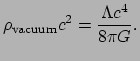 |
(394) |
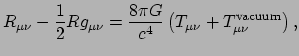 |
(395) |
Als
![]() , dan dient hij op zijn minst zó klein te zijn
dat
, dan dient hij op zijn minst zó klein te zijn
dat
![]() verwaarloosbare gravitationele effecten heeft
(
verwaarloosbare gravitationele effecten heeft
(
![]() voor gevallen
waarbij de newtoniaanse gravitatietheorie een goede beschrijving van de
meetgegevens geeft. De systemen met kleinste dichtheid waarop de wetten
van Newton worden toegepast, zijn kleine clusters van sterrenstelsels.
Hiermee kunnen we de volgende limiet plaatsen
voor gevallen
waarbij de newtoniaanse gravitatietheorie een goede beschrijving van de
meetgegevens geeft. De systemen met kleinste dichtheid waarop de wetten
van Newton worden toegepast, zijn kleine clusters van sterrenstelsels.
Hiermee kunnen we de volgende limiet plaatsen
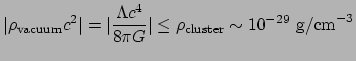 |
(396) |
![\includegraphics[width=12cm]{Figures/type1a.eps}](img1654.png)
|
Hoe kunnen we de energiedichtheid van het vacuum berekenen? De eenvoudigste
berekeningen sommeren de quantummechanische nulpuntsenergie van alle in
de natuur bekende velden op. Het antwoord dat gevonden wordt is ongeveer
120 ordes van grootte hoger dan de bovengrens op ![]() die we
net bepaald hebben. Dit is niet begrepen en er dient een fysisch mechanisme
te bestaan dat de kosmologische constante klein maakt. Recente meetgegevens
duiden erop dat de kosmologische constante niet precies gelijk is aan nul.
De sterkste aanwijzing komt van metingen aan verre Type Ia supernovae, die
zeggen dat de expansie van het universum op dit moment toeneemt.
Dit wordt getoond in Fig. 56.
Zonder kosmologische constante verwachten we dat door de aantrekkende kracht
van alle materie in het universum, de expansie zou vertragen en misschien
zelfs aanleiding zou geven voor een contractie van het universum. Als
de kosmologische constante echter van nul verschilt, kan de negatieve
druk van het vacuum veroorzaken dat het universum versnelt uitdijt.
die we
net bepaald hebben. Dit is niet begrepen en er dient een fysisch mechanisme
te bestaan dat de kosmologische constante klein maakt. Recente meetgegevens
duiden erop dat de kosmologische constante niet precies gelijk is aan nul.
De sterkste aanwijzing komt van metingen aan verre Type Ia supernovae, die
zeggen dat de expansie van het universum op dit moment toeneemt.
Dit wordt getoond in Fig. 56.
Zonder kosmologische constante verwachten we dat door de aantrekkende kracht
van alle materie in het universum, de expansie zou vertragen en misschien
zelfs aanleiding zou geven voor een contractie van het universum. Als
de kosmologische constante echter van nul verschilt, kan de negatieve
druk van het vacuum veroorzaken dat het universum versnelt uitdijt.