Het formalisme dat we in de vorige sectie besproken hebben, heeft geen eigenschappen
van de metrische tensor gebruikt in het opstellen van de covariante afgeleiden.
De metriek kan vectoren veranderen in 1-vormen en omgekeerd, en we verwachten daarom
dat deze een rol speelt in het verband tussen hun afgeleiden. In het geval van cartesische
coördinaten zijn de componenten van de 1-vorm en de eraan gerelateerde vector gelijk,
en omdat ![]() dan enkel het nemen van afgeleiden van componenten is, moeten de
componenten van de covariante afgeleide van de 1-vorm en vector gelijk zijn
aan elkaar. Dit betekent dat als
dan enkel het nemen van afgeleiden van componenten is, moeten de
componenten van de covariante afgeleide van de 1-vorm en vector gelijk zijn
aan elkaar. Dit betekent dat als ![]() een willekeurige vector is en
een willekeurige vector is en
![]() de eraan gerelateerde 1-vorm, dan geldt in cartesische coördinaten
de eraan gerelateerde 1-vorm, dan geldt in cartesische coördinaten
Als de hierboven gevolgde argumentatie niet bevredigend is, dan kunnen we er
met vergelijkingen nog eens door heen lopen. De indices ![]() ,
, ![]() ,
, ![]() , ...
geven cartesische coördinaten aan, terwijl de indices met accenten
, ...
geven cartesische coördinaten aan, terwijl de indices met accenten
![]() ,
,
![]() ,
,
![]() , ... willekeurige coördinaten
aangeven. We beginnen met het statement
, ... willekeurige coördinaten
aangeven. We beginnen met het statement
![]() ,
dat geldig is in elk coördinatenstelsel. Echter in cartesische coördinaten
geldt
,
dat geldig is in elk coördinatenstelsel. Echter in cartesische coördinaten
geldt
![]() en
en
![]() . Nu is het ook zo
dat in cartesische coördinaten de christoffelsymbolen allemaal gelijk zijn aan nul.
Dus hebben we
. Nu is het ook zo
dat in cartesische coördinaten de christoffelsymbolen allemaal gelijk zijn aan nul.
Dus hebben we
![]() en
en
![]() . We kunnen daarom concluderen dat
. We kunnen daarom concluderen dat
![]() , enkel in cartesische coördinaten.
Om dit om te zetten in een vergelijking die geldig is in alle coördinatenstelsels,
merken we op dat in cartesische coördinaten geldt dat
, enkel in cartesische coördinaten.
Om dit om te zetten in een vergelijking die geldig is in alle coördinatenstelsels,
merken we op dat in cartesische coördinaten geldt dat
![]() , zodat, ook weer in cartesische
coördinaten, geldt dat
, zodat, ook weer in cartesische
coördinaten, geldt dat
![]() .
Deze vergelijking is een tensorvergelijking, zodat geldigheid ervan in één
coördinatenstelsel de geldigheid in alle stelsels impliceert. We vinden dan
weer vergelijking (287),
.
Deze vergelijking is een tensorvergelijking, zodat geldigheid ervan in één
coördinatenstelsel de geldigheid in alle stelsels impliceert. We vinden dan
weer vergelijking (287),
Voorbeeld: afgeleiden van de metrische tensor.
We starten met vergelijking (285), en schrijven
| (286) |
| (287) |
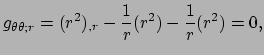 |
(288) |
Wat we hierboven gedaan hebben is het introduceren van covariante differentiatie
in willekeurige coördinaten door ons begrip van parallelheid in de euclidische
ruimte te gebruiken. We hebben laten zien dat de metriek van de euclidische
ruimte covariant constant is, vergelijking (290). Als we
gekromde ruimten gaan behandelen, dienen we voorzichtig te zijn met het
begrip parallelheid, maar vergelijking (290) zal blijken
nog steeds te gelden, en dus ook alle consequenties ervan die we nu gaan bespreken.