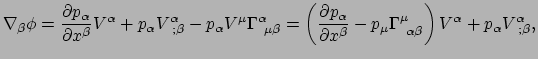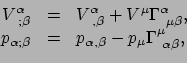Next: Christoffelsymbolen en de metriek
Up: Wiskunde II - Curvelineaire
Previous: Vectoren en 1-vormen
Contents
Stel we hebben een vector  waarvan de componenten
waarvan de componenten 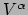 gegeven zijn ten opzichte
van een willekeurig coördinatenstelsel
gegeven zijn ten opzichte
van een willekeurig coördinatenstelsel
 . We willen nu de afgeleide
van deze vector bepalen. Er geldt
. We willen nu de afgeleide
van deze vector bepalen. Er geldt
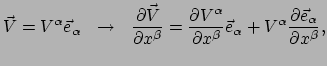 |
(259) |
waarbij 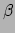 gelijk is aan 0 of
gelijk is aan 0 of 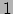 , etc.
De laatste term wordt veroorzaakt doordat de basisvectoren niet overal constant
hoeven te zijn. Omdat
, etc.
De laatste term wordt veroorzaakt doordat de basisvectoren niet overal constant
hoeven te zijn. Omdat
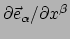 zelf een vector is,
kunnen we deze schrijven als een lineaire combinatie van basisvectoren. Hiertoe
introduceren we het symbool
zelf een vector is,
kunnen we deze schrijven als een lineaire combinatie van basisvectoren. Hiertoe
introduceren we het symbool
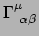 om de coëfficiënten
aan te duiden. Er geldt
om de coëfficiënten
aan te duiden. Er geldt
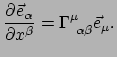 |
(260) |
De interpretatie van
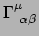 is dat het de
is dat het de 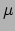 -de component
van
-de component
van
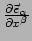 voorstelt. Dit object heet een
christoffelsymbool en heeft drie indices: de eerste (
voorstelt. Dit object heet een
christoffelsymbool en heeft drie indices: de eerste (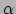 ) geeft de
basisvector aan die wordt gedifferentieerd; de tweede (
) geeft de
basisvector aan die wordt gedifferentieerd; de tweede (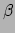 ) geeft de coördinaat
aan waarnaar wordt gedifferentieerd; en de derde (
) geeft de coördinaat
aan waarnaar wordt gedifferentieerd; en de derde (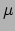 ) geeft de component van
de resulterende afgeleide vector aan. Alle indices dienen te refereren naar hetzelfde
coördinatenstelsel.
) geeft de component van
de resulterende afgeleide vector aan. Alle indices dienen te refereren naar hetzelfde
coördinatenstelsel.
Met bovenstaande definitie van de christoffelsymbolen kunnen we vergelijking
(265) schrijven als
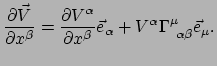 |
(261) |
De laatste term bevat twee sommaties (over 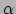 en
en 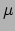 ) en als we de bijbehorende
dummie indices herlabelen, vinden we
) en als we de bijbehorende
dummie indices herlabelen, vinden we
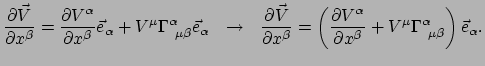 |
(262) |
We zien dat het vectorveld
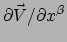 de componenten
de componenten
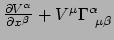 heeft.
Merk op dat we voor partiële afgeleiden reeds de komma-notatie gebruiken,
heeft.
Merk op dat we voor partiële afgeleiden reeds de komma-notatie gebruiken,
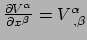 . We definiëren
een nieuwe notatie
. We definiëren
een nieuwe notatie
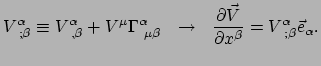 |
(263) |
Nu is
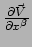 een vectorveld als we de index
een vectorveld als we de index 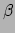 opvatten als één vast getal. Deze index kan echter meer waarden aannemen
en we kunnen
opvatten als één vast getal. Deze index kan echter meer waarden aannemen
en we kunnen
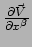 dan ook beschouwen als
zijnde geassocieerd met een
dan ook beschouwen als
zijnde geassocieerd met een
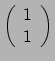 tensorveld dat de vector
tensorveld dat de vector
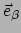 afbeeldt op de vector
afbeeldt op de vector
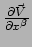 . Dit tensorveld wordt de
covariante afgeleide van
. Dit tensorveld wordt de
covariante afgeleide van  genoemd64 en aangeduid met
genoemd64 en aangeduid met
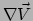 .
Haar componenten zijn
.
Haar componenten zijn
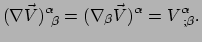 |
(264) |
Op een cartesische basis zijn de componenten gelijk aan
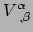 omdat
dan de vectorvelden van de basis constant zijn. Op een gekromde basis moeten
we rekening houden met de afgeleiden van de basisvectoren en krijgen we
omdat
dan de vectorvelden van de basis constant zijn. Op een gekromde basis moeten
we rekening houden met de afgeleiden van de basisvectoren en krijgen we
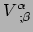 als componenten van
als componenten van
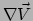 in het coördinatensysteem
waaraan de christoffelsymbolen refereren. Er bestaat één enkele
in het coördinatensysteem
waaraan de christoffelsymbolen refereren. Er bestaat één enkele
 tensor die we
tensor die we
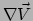 noemen. In cartesische coördinaten zijn de componenten
gelijk aan
noemen. In cartesische coördinaten zijn de componenten
gelijk aan
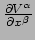 . In algemene
coördinaten
. In algemene
coördinaten
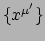 worden de componenten
worden de componenten
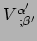 genoemd. We kunnen deze componenten op de
volgende manieren vinden: (i) reken ze direct uit met behulp van vergelijking
(269) hetgeen kennis vereist van de christoffelsymbolen voor dit
coördinatenstelsel; of (ii) verkrijg ze via de gebruikelijke tensortransformatie
vanuit een cartesisch systeem naar
genoemd. We kunnen deze componenten op de
volgende manieren vinden: (i) reken ze direct uit met behulp van vergelijking
(269) hetgeen kennis vereist van de christoffelsymbolen voor dit
coördinatenstelsel; of (ii) verkrijg ze via de gebruikelijke tensortransformatie
vanuit een cartesisch systeem naar
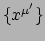 . We demonstreren de
eerste methode aan de hand van een voorbeeld.
. We demonstreren de
eerste methode aan de hand van een voorbeeld.
Voorbeeld: tensorcalculus in poolcoördinaten.
In poolcoördinaten is het vectorveld 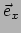 constant: hetzelfde op
elk punt. In poolcoördinaten heeft dit veld de componenten
constant: hetzelfde op
elk punt. In poolcoördinaten heeft dit veld de componenten
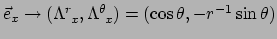 .
Deze componenten zijn duidelijk niet constant, terwijl
.
Deze componenten zijn duidelijk niet constant, terwijl 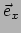 dat wel is. Dit komt
omdat de componenten refereren naar een niet constante basis. Als we deze
componenten zouden differentiëren naar, zeg,
dat wel is. Dit komt
omdat de componenten refereren naar een niet constante basis. Als we deze
componenten zouden differentiëren naar, zeg, 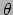 , dan vinden we
zeker niet
, dan vinden we
zeker niet
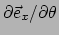 , want dat dient
gelijk te zijn aan nul. We zien dus dat enkel het nemen van de afgeleide van de componenten
van een vector niet de afgeleide van de vector oplevert. We dienen ook de
niet-constante basisvectoren te differentiëren, in overeenstemming met
vergelijking (265). Omdat de cartesische basisvectoren
, want dat dient
gelijk te zijn aan nul. We zien dus dat enkel het nemen van de afgeleide van de componenten
van een vector niet de afgeleide van de vector oplevert. We dienen ook de
niet-constante basisvectoren te differentiëren, in overeenstemming met
vergelijking (265). Omdat de cartesische basisvectoren 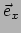 en
en 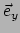 constante velden zijn (en hun afgeleiden dus verdwijnen) vinden we
constante velden zijn (en hun afgeleiden dus verdwijnen) vinden we
Evenzo vinden we
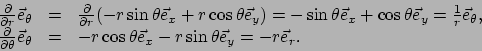 |
(266) |
We kunnen nu de afgeleide
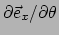 uitrekenen
en vinden
uitrekenen
en vinden
Vereenvoudigen levert
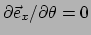 zoals we verwachten.
zoals we verwachten.
We kunnen ook de christoffelsymbolen berekenen en vinden
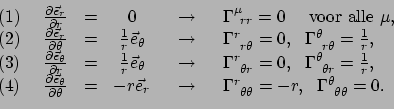 |
(268) |
We zien dat alle indices naar hetzelfde coördinatenstelsel refereren.
De covariante afgeleide verschilt enkel van de partiële afgeleide
als de basisvectoren niet constant zijn. Een scalairveld 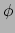 hangt echter niet
van de basisvectoren af en dus is haar covariante afgeleide gelijk aan haar
partiële afgeleide en dat is de gradiënt,
hangt echter niet
van de basisvectoren af en dus is haar covariante afgeleide gelijk aan haar
partiële afgeleide en dat is de gradiënt,
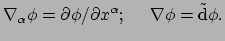 |
(269) |
Vervolgens beschouwen we de divergentie en Laplace operatoren.
In cartesische coördinaten is de divergentie van een vector 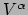 gelijk aan
gelijk aan
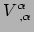 . Dit is een getal (scalairveld) dat we krijgen
door contractie van de indices van
. Dit is een getal (scalairveld) dat we krijgen
door contractie van de indices van
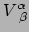 . Deze contractie (dit getal dus) hangt
niet van het coördinatenstelsel af en we kunnen de divergentie van
. Deze contractie (dit getal dus) hangt
niet van het coördinatenstelsel af en we kunnen de divergentie van  dan ook uitrekenen in andere coördinaten
dan ook uitrekenen in andere coördinaten
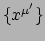 door weer de
componenten van
door weer de
componenten van
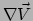 te contraheren over haar twee indices. Het
resultaat is een getal met de waarde
te contraheren over haar twee indices. Het
resultaat is een getal met de waarde
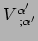 .
Het is belangrijk om in te zien dat dit hetzelfde getal is als
.
Het is belangrijk om in te zien dat dit hetzelfde getal is als
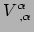 in cartesische coördinaten. Dus
in cartesische coördinaten. Dus
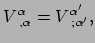 |
(270) |
waarbij de normale indices refereren naar cartesische coördinaten, terwijl
die met accenten refereren naar een willekeurig systeem.
Wellicht is de lezer vertrouwder met de Laplace operator en dat is de
divergentie van de gradiënt. Vergelijking (276) geeft de
divergentie van een vector, terwijl de gradiënt een 1-vorm is. We dienen
deze 1-vorm dus eerst om te schrijven in een vector. We zullen dit weer
uitwerken aan de hand van een voorbeeld.
Voorbeeld: divergentie en Laplace operator in poolcoördinaten.
In poolcoördinaten hebben we voor de divergentie
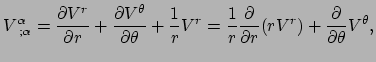 |
(271) |
waarbij we vergelijking (269) en de verschillende christoffelsymbolen
in poolcoördinaten (vergelijking (274)) gebruikt hebben.
Teneinde de Laplace operator te vinden, starten we met een scalairveld 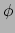 en bepalen we de vector gradiënt. Dat is reeds gebeurd in vergelijking (264).
We vullen deze vector in in vergelijking (277) en vinden
en bepalen we de vector gradiënt. Dat is reeds gebeurd in vergelijking (264).
We vullen deze vector in in vergelijking (277) en vinden
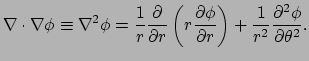 |
(272) |
Dit is de Laplace operator is euclidische poolcoördinaten en deze is
identiek aan
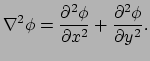 |
(273) |
Ter afronding bekijken we de afgeleiden van 1-vormen en hogere-orde tensorvelden.
Om de afgeleide van een 1-vorm te vinden gebruiken we de eigenschap dat een
1-vorm en vector samen een scalair geven. Dus als 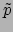 een 1-vorm is
en
een 1-vorm is
en  een vector, dan is voor gegeven
een vector, dan is voor gegeven 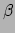 ,
,
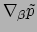 ook een 1-vorm,
ook een 1-vorm,
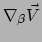 een vector, en
een vector, en
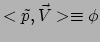 een scalair. In een willekeurig coördinatenstelsel wordt deze scalair
geschreven als
een scalair. In een willekeurig coördinatenstelsel wordt deze scalair
geschreven als
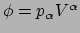 . Daarom geldt voor
. Daarom geldt voor
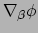 volgens de productregel voor afgeleiden
volgens de productregel voor afgeleiden
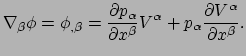 |
(274) |
We kunnen vergelijking (269) gebruiken om
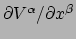 te vervangen door
te vervangen door
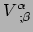 hetgeen de componenten zijn van
hetgeen de componenten zijn van
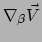 en vinden
en vinden
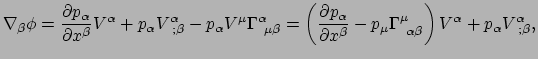 |
(275) |
waarbij we in de laatste stap termen verwisseld hebben en dummie indices andere
namen gegeven. Van iedere term in bovenstaande vergelijking weten we dat het een
tensorcomponent is voor willekeurige  , behalve van die tussen haakjes.
Omdat vermenigvuldigen en optellen van tensorcomponenten altijd nieuwe
tensoren oplevert, moet het zo zijn dat de term tussen haakjes ook een tensor is.
Dit is de covariante afgeleide van
, behalve van die tussen haakjes.
Omdat vermenigvuldigen en optellen van tensorcomponenten altijd nieuwe
tensoren oplevert, moet het zo zijn dat de term tussen haakjes ook een tensor is.
Dit is de covariante afgeleide van 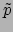 . Er geldt dus
. Er geldt dus
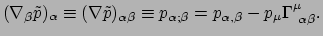 |
(276) |
Verder geldt
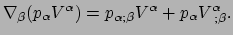 |
(277) |
We zien dat covariant differentiëren aan dezelfde soort productregel voldoet
als vergelijking (280). Dit kan ook niet anders, want in cartesische coördinaten
staat 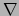 voor partiëel differentiëren van componenten.
voor partiëel differentiëren van componenten.
We kunnen nu de volgende uitdrukkingen vergelijken.
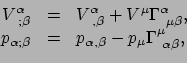 |
(278) |
en zien enkele overeenkomsten en enkele verschillen. We herinneren ons dat
de laatste index van het christoffelsymbool de differentiatie index is. Dit betekent
dat enkel de andere indices met de metriek naar boven of beneden kunnen worden gehaald.
Wat er dan nog overblijft is het tekenverschil. Hierbij helpt het om zich te
herinneren dat
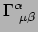 te maken had met afgeleiden van
basisvectoren. Het lijkt daarom redelijk te veronderstellen dat
te maken had met afgeleiden van
basisvectoren. Het lijkt daarom redelijk te veronderstellen dat
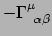 te maken heeft met afgeleiden van basis 1-vormen.
De tekenverandering duidt erop dat de basis 1-vormen tegenovergesteld veranderen
aan de basisvectoren, hetgeen redelijk is als we beseffen dat de
contractie
te maken heeft met afgeleiden van basis 1-vormen.
De tekenverandering duidt erop dat de basis 1-vormen tegenovergesteld veranderen
aan de basisvectoren, hetgeen redelijk is als we beseffen dat de
contractie
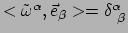 een constante is met afgeleide nul.
een constante is met afgeleide nul.
Dezelfde procedure leidt ook tot
We zien dat deze uitdrukkingen een bepaalde systematiek hebben. Zo is er een 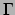 term
voor elke index; een boven index wordt als een vector behandeld en een beneden index als
een 1-vorm.
term
voor elke index; een boven index wordt als een vector behandeld en een beneden index als
een 1-vorm.




Next: Christoffelsymbolen en de metriek
Up: Wiskunde II - Curvelineaire
Previous: Vectoren en 1-vormen
Contents
Jo van den Brand
2009-01-31
![]() waarvan de componenten
waarvan de componenten ![]() gegeven zijn ten opzichte
van een willekeurig coördinatenstelsel
gegeven zijn ten opzichte
van een willekeurig coördinatenstelsel
![]() . We willen nu de afgeleide
van deze vector bepalen. Er geldt
. We willen nu de afgeleide
van deze vector bepalen. Er geldt
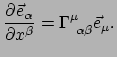
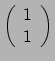 tensorveld dat de vector
tensorveld dat de vector
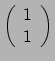 tensor die we
tensor die we
![]() constant: hetzelfde op
elk punt. In poolcoördinaten heeft dit veld de componenten
constant: hetzelfde op
elk punt. In poolcoördinaten heeft dit veld de componenten
![]() .
Deze componenten zijn duidelijk niet constant, terwijl
.
Deze componenten zijn duidelijk niet constant, terwijl ![]() dat wel is. Dit komt
omdat de componenten refereren naar een niet constante basis. Als we deze
componenten zouden differentiëren naar, zeg,
dat wel is. Dit komt
omdat de componenten refereren naar een niet constante basis. Als we deze
componenten zouden differentiëren naar, zeg, ![]() , dan vinden we
zeker niet
, dan vinden we
zeker niet
![]() , want dat dient
gelijk te zijn aan nul. We zien dus dat enkel het nemen van de afgeleide van de componenten
van een vector niet de afgeleide van de vector oplevert. We dienen ook de
niet-constante basisvectoren te differentiëren, in overeenstemming met
vergelijking (265). Omdat de cartesische basisvectoren
, want dat dient
gelijk te zijn aan nul. We zien dus dat enkel het nemen van de afgeleide van de componenten
van een vector niet de afgeleide van de vector oplevert. We dienen ook de
niet-constante basisvectoren te differentiëren, in overeenstemming met
vergelijking (265). Omdat de cartesische basisvectoren ![]() en
en ![]() constante velden zijn (en hun afgeleiden dus verdwijnen) vinden we
constante velden zijn (en hun afgeleiden dus verdwijnen) vinden we
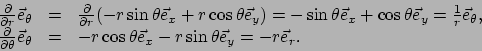
![]() hangt echter niet
van de basisvectoren af en dus is haar covariante afgeleide gelijk aan haar
partiële afgeleide en dat is de gradiënt,
hangt echter niet
van de basisvectoren af en dus is haar covariante afgeleide gelijk aan haar
partiële afgeleide en dat is de gradiënt,
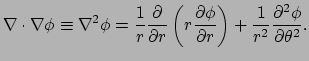
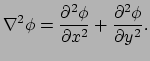
![]() een 1-vorm is
en
een 1-vorm is
en ![]() een vector, dan is voor gegeven
een vector, dan is voor gegeven ![]() ,
,
![]() ook een 1-vorm,
ook een 1-vorm,
![]() een vector, en
een vector, en
![]() een scalair. In een willekeurig coördinatenstelsel wordt deze scalair
geschreven als
een scalair. In een willekeurig coördinatenstelsel wordt deze scalair
geschreven als
![]() . Daarom geldt voor
. Daarom geldt voor
![]() volgens de productregel voor afgeleiden
volgens de productregel voor afgeleiden