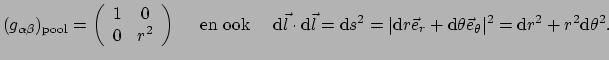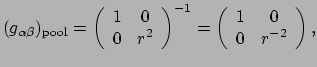Next: Tensorcalculus
Up: Wiskunde II - Curvelineaire
Previous: Wiskunde II - Curvelineaire
Contents
De traditionele manier waarop een vector gedefinieerd wordt, is door te stellen dat
hij onder willekeurige coördinatentransformaties op dezelfde manier transformeert
als de verplaatsing. Hiermee bedoelen we dat een vector
 voorgesteld
kan worden als een verplaatsing
voorgesteld
kan worden als een verplaatsing
 , of in poolcoördinaten
als
, of in poolcoördinaten
als
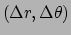 , of in het algemeen door
, of in het algemeen door
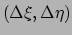 .
Voor kleine
.
Voor kleine
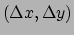 geldt dan
geldt dan
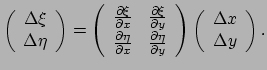 |
(239) |
We stellen nu dat een willekeurige vector  op precies dezelfde manier
dient te transformeren. Dus geldt
op precies dezelfde manier
dient te transformeren. Dus geldt
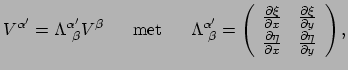 |
(240) |
waarbij de index 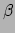 refereert aan het systeem
refereert aan het systeem 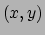 en
index
en
index
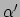 aan het systeem
aan het systeem
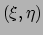 .
.
Er is een moderne en meer natuurlijke manier om vectoren en 1-vormen te introduceren.
Hiertoe beschouwen we een scalair veld 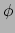 . Gegeven de coördinaten
. Gegeven de coördinaten
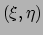 is het altijd mogelijk om de afgeleiden
is het altijd mogelijk om de afgeleiden
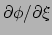 en
en
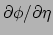 te vormen. We definiëren de
1-vorm
te vormen. We definiëren de
1-vorm
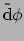 als het geometrisch object met componenten
als het geometrisch object met componenten
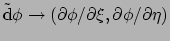 |
(241) |
in het coördinatenstelsel
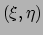 . Dit is algemene definitie van
een oneindig aantal 1-vormen, elk voor een ander scalair veld. De transformatie
van de componenten volgt uit de kettingregel,
. Dit is algemene definitie van
een oneindig aantal 1-vormen, elk voor een ander scalair veld. De transformatie
van de componenten volgt uit de kettingregel,
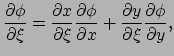 |
(242) |
en evenzo voor
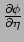 . We vinden hiermee
. We vinden hiermee
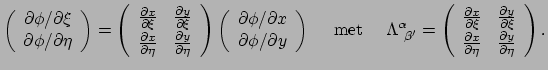 |
(243) |
We zien dat componenten van 1-vormen transformeren met
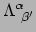 en
dat is tegenovergesteld aan het transformatiegedrag van vectorcomponenten, zoals
gegeven in vergelijking (246).61
en
dat is tegenovergesteld aan het transformatiegedrag van vectorcomponenten, zoals
gegeven in vergelijking (246).61
We beschouwen nu de afgeleide van een scalair veld 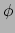 langs een curve
langs een curve
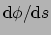 (zie ook sectie 4.5.2). Deze hangt af
van de parameter
(zie ook sectie 4.5.2). Deze hangt af
van de parameter 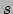 en als we die veranderen, dan verandert ook de afgeleide.
We kunnen dit schrijven als
en als we die veranderen, dan verandert ook de afgeleide.
We kunnen dit schrijven als
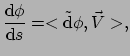 |
(245) |
met  de vector met componenten
de vector met componenten
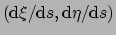 .
Deze vector hangt enkel van de curve af, terwijl
.
Deze vector hangt enkel van de curve af, terwijl
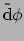 enkel
van
enkel
van 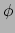 afhangt. Daarom is
afhangt. Daarom is  karakteristiek voor de curve
en wordt de tangent vector genoemd. We kunnen een vector dus
opvatten als een object dat
karakteristiek voor de curve
en wordt de tangent vector genoemd. We kunnen een vector dus
opvatten als een object dat
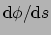 produceert als
produceert als
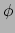 gegeven is. Dit leidt tot de moderne opvatting dat een tangent
vector aan een curve
gegeven is. Dit leidt tot de moderne opvatting dat een tangent
vector aan een curve
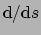 genoemd moet worden62.
Elke curve (met parameter
genoemd moet worden62.
Elke curve (met parameter 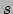 ) heeft een tangent vector
) heeft een tangent vector  gedefinieerd als een lineaire functie die een 1-vorm als argument
neemt en afbeeldt naar het reële getal
gedefinieerd als een lineaire functie die een 1-vorm als argument
neemt en afbeeldt naar het reële getal
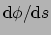 .
.
Onder een coördinatentransformatie gebeurt er niets met 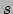 (de definitie
van deze parameter had niets met coördinaten te maken), maar veranderen
de componenten van
(de definitie
van deze parameter had niets met coördinaten te maken), maar veranderen
de componenten van  volgens de kettingregel als
volgens de kettingregel als
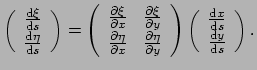 |
(251) |
Dit is dezelfde transformatiewet die we eerder voor vectoren hebben gevonden;
vergelijk dit met uitdrukking (246) en op basis van deze correspondentie
mogen we  een vector noemen. Met deze informatie kunnen we onze
beschouwing in poolcoördinaten voorzetten.
een vector noemen. Met deze informatie kunnen we onze
beschouwing in poolcoördinaten voorzetten.
Voorbeeld: basis 1-vormen en vectoren in poolcoördinaten.
Voor de basiscoördinaten geldt
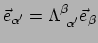 en dit levert
en dit levert
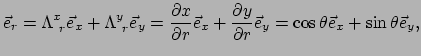 |
(252) |
en op dezelfde wijze
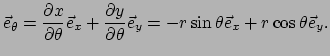 |
(253) |
Merk op dat we gebruiken dat
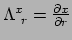 .
Op dezelfde wijze kunnen we de andere kant op transformeren met
.
Op dezelfde wijze kunnen we de andere kant op transformeren met
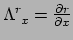 .
De transformatiematrices zijn eenvoudig: we hoeven enkel te kijken naar welke index
boven of beneden is en we weten welke afgeleide we dienen te gebruiken.
.
De transformatiematrices zijn eenvoudig: we hoeven enkel te kijken naar welke index
boven of beneden is en we weten welke afgeleide we dienen te gebruiken.
De basis 1-vormen vinden we op analoge wijze. Er geldt
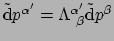 en dus
en dus
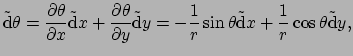 |
(254) |
en ook
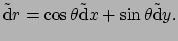 |
(255) |
Figuur 45:
Links: basisvectoren voor poolcoördinaten; rechts: basis 1-vormen.
|
|
In Fig. 45 trachten we de basisvectoren en 1-vormen grafisch
weer te geven. We tekenen de 1-vormen door oppervlakken te tekenen met constante
 of
of  voor respectievelijk
voor respectievelijk
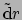 en
en
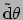 .
Merk op dat de bases veranderen van punt tot punt! Ook de lengten van de bases
zijn niet constant. We vinden bijvoorbeeld
.
Merk op dat de bases veranderen van punt tot punt! Ook de lengten van de bases
zijn niet constant. We vinden bijvoorbeeld
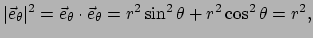 zodat de lengte van
zodat de lengte van
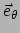 toeneemt met haar afstand tot de oorsprong. We hebben dus
ook geen eenheidsbasis meer. Er geldt
toeneemt met haar afstand tot de oorsprong. We hebben dus
ook geen eenheidsbasis meer. Er geldt
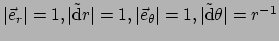 .
.
De inproducten kunnen worden uitgerekend, omdat we de metriek in cartesische
coördinaten  kennen:
kennen:
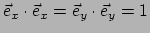 en
en
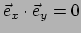 . In tensornotatie is dat
. In tensornotatie is dat
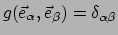 voor cartesische coördinaten.
De metriek g in poolcoördinaten heeft de componenten
voor cartesische coördinaten.
De metriek g in poolcoördinaten heeft de componenten
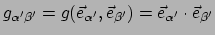 en dit levert
en dit levert
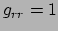 ,
,
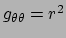 en
en
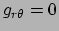 . We kunnen de componenten
van
. We kunnen de componenten
van 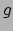 ook schrijven als
ook schrijven als
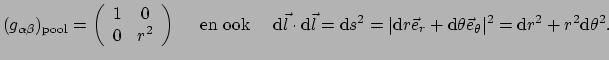 |
(256) |
De laatste formule in bovenstaande uitdrukking63
geeft de lengte van een willekeurige
en oneindig kleine verplaatsing
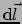 , hetgeen een handige manier is om de
componenten van de metrische tensor en tegelijkertijd de coördinaten van het
lijnelement
, hetgeen een handige manier is om de
componenten van de metrische tensor en tegelijkertijd de coördinaten van het
lijnelement
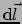 te tonen.
te tonen.
De metriek heeft een inverse
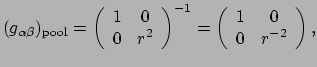 |
(257) |
waarmee geldt dat
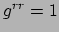 ,
,
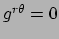 en
en
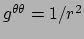 . We kunnen
dit gebruiken om een afbeelding te maken tussen vectoren en 1-vormen. Stel bijvoorbeeld
dat
. We kunnen
dit gebruiken om een afbeelding te maken tussen vectoren en 1-vormen. Stel bijvoorbeeld
dat 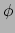 een scalairveld is en
een scalairveld is en
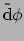 haar gradiënt, dan heeft de
vector
haar gradiënt, dan heeft de
vector
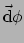 de componenten
de componenten
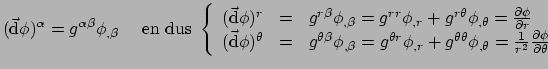 |
(258) |
Dus terwijl
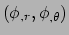 componenten van een 1-vorm zijn, heeft de
vector gradiënt componenten
componenten van een 1-vorm zijn, heeft de
vector gradiënt componenten
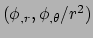 . Ondanks dat we in de euclidische
ruimte zijn, zien we dat vectoren in het algemeen componenten hebben die verschillen van
die van de geassocieerde 1-vormen. Cartesische coördinaten zijn de enige coördinaten
waarvoor de componenten hetzelfde zijn (want
. Ondanks dat we in de euclidische
ruimte zijn, zien we dat vectoren in het algemeen componenten hebben die verschillen van
die van de geassocieerde 1-vormen. Cartesische coördinaten zijn de enige coördinaten
waarvoor de componenten hetzelfde zijn (want
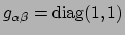 ).
).




Next: Tensorcalculus
Up: Wiskunde II - Curvelineaire
Previous: Wiskunde II - Curvelineaire
Contents
Jo van den Brand
2009-01-31
![]() voorgesteld
kan worden als een verplaatsing
voorgesteld
kan worden als een verplaatsing
![]() , of in poolcoördinaten
als
, of in poolcoördinaten
als
![]() , of in het algemeen door
, of in het algemeen door
![]() .
Voor kleine
.
Voor kleine
![]() geldt dan
geldt dan
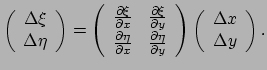
![]() . Gegeven de coördinaten
. Gegeven de coördinaten
![]() is het altijd mogelijk om de afgeleiden
is het altijd mogelijk om de afgeleiden
![]() en
en
![]() te vormen. We definiëren de
1-vorm
te vormen. We definiëren de
1-vorm
![]() als het geometrisch object met componenten
als het geometrisch object met componenten
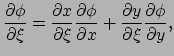
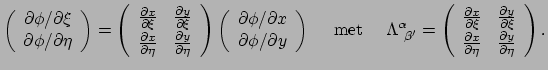
![]() langs een curve
langs een curve
![]() (zie ook sectie 4.5.2). Deze hangt af
van de parameter
(zie ook sectie 4.5.2). Deze hangt af
van de parameter ![]() en als we die veranderen, dan verandert ook de afgeleide.
We kunnen dit schrijven als
en als we die veranderen, dan verandert ook de afgeleide.
We kunnen dit schrijven als
![]() (de definitie
van deze parameter had niets met coördinaten te maken), maar veranderen
de componenten van
(de definitie
van deze parameter had niets met coördinaten te maken), maar veranderen
de componenten van ![]() volgens de kettingregel als
volgens de kettingregel als
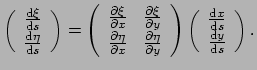
![]() en dit levert
en dit levert
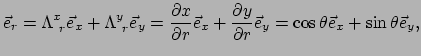
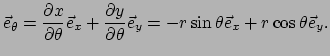
![]() en dus
en dus
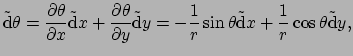
![]() of
of ![]() voor respectievelijk
voor respectievelijk
![]() en
en
![]() .
Merk op dat de bases veranderen van punt tot punt! Ook de lengten van de bases
zijn niet constant. We vinden bijvoorbeeld
.
Merk op dat de bases veranderen van punt tot punt! Ook de lengten van de bases
zijn niet constant. We vinden bijvoorbeeld
![]() zodat de lengte van
zodat de lengte van
![]() toeneemt met haar afstand tot de oorsprong. We hebben dus
ook geen eenheidsbasis meer. Er geldt
toeneemt met haar afstand tot de oorsprong. We hebben dus
ook geen eenheidsbasis meer. Er geldt
![]() .
.
![]() kennen:
kennen:
![]() en
en
![]() . In tensornotatie is dat
. In tensornotatie is dat
![]() voor cartesische coördinaten.
De metriek g in poolcoördinaten heeft de componenten
voor cartesische coördinaten.
De metriek g in poolcoördinaten heeft de componenten
![]() en dit levert
en dit levert
![]() ,
,
![]() en
en
![]() . We kunnen de componenten
van
. We kunnen de componenten
van ![]() ook schrijven als
ook schrijven als