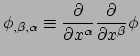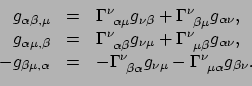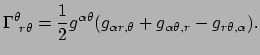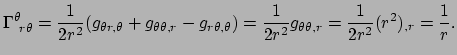Next: De algemene relativiteitstheorie
Up: Christoffelsymbolen en de metriek
Previous: Christoffelsymbolen en de metriek
Contents
Vergelijking (291) leidt tot een uiterst belangrijk resultaat: we
kunnen deze vergelijking gebruiken om
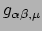 te bepalen in termen
van
te bepalen in termen
van
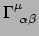 . Het omgekeerde blijkt ook waar te zijn:
. Het omgekeerde blijkt ook waar te zijn:
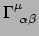 uitdrukken in termen van
uitdrukken in termen van
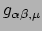 .
Dat geeft een eenvoudige manier om de christoffelsymbolen uit te rekenen.
We moeten eerst echter de relatie
.
Dat geeft een eenvoudige manier om de christoffelsymbolen uit te rekenen.
We moeten eerst echter de relatie
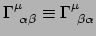 bewijzen, die geldt in elk coördinatenstelsel.
Om deze symmetrie te bewijzen beschouwen we een willekeurig scalairveld
bewijzen, die geldt in elk coördinatenstelsel.
Om deze symmetrie te bewijzen beschouwen we een willekeurig scalairveld 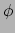 .
De eerste afgeleide
.
De eerste afgeleide
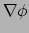 is een 1-vorm met componenten
is een 1-vorm met componenten
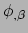 .
De tweede covariante afgeleide
.
De tweede covariante afgeleide
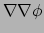 heeft componenten
heeft componenten
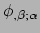 en is een
en is een
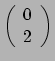 tensor. In cartesische
coördinaten zijn de componenten
tensor. In cartesische
coördinaten zijn de componenten
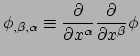 |
(289) |
en we zien dat deze symmetrisch zijn in 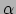 en
en 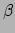 , omdat partiële
afgeleiden commuteren. Echter als een tensor symmetrisch is in één basis,
dan is hij symmetrisch in alle bases. Dus geldt
, omdat partiële
afgeleiden commuteren. Echter als een tensor symmetrisch is in één basis,
dan is hij symmetrisch in alle bases. Dus geldt
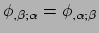 |
(290) |
in elke basis. Gebruikmaken van de definitie gegeven in vergelijking (282)
levert
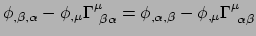 |
(291) |
in elk coördinatensysteem. Maar er geldt
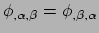 en dit levert
en dit levert
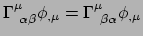 |
(292) |
voor willekeurige 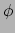 . Hiermee is bewezen dat in elk coördinatenstelsel
. Hiermee is bewezen dat in elk coördinatenstelsel
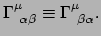 |
(293) |
We gebruiken bovenstaande symmetrie om vergelijking (291) te inverteren.
Dat is tevens een mooi voorbeeld van geavanceerde index-manipulatie.
Hiertoe schrijven we vergelijking (291) in drie permutaties van
de indices,
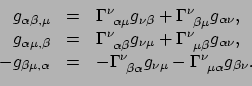 |
(294) |
We tellen deze op, groeperen termen, gebruiken de symmetrie van 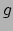 ,
,
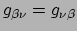 en vinden
en vinden
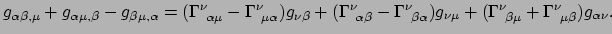 |
(295) |
In deze vergelijking vallen de eerste twee termen rechts weg vanwege de
symmetrie van 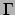 en vinden we
en vinden we
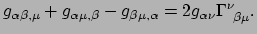 |
(296) |
Delen door 2, vermenigvuldigen met
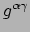 (en sommeren over
(en sommeren over
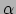 ), en gebruik maken van
), en gebruik maken van
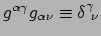 levert
levert
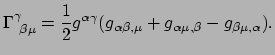 |
(297) |
Dit is de uitdrukking voor de christoffelsymbolen in termen van de
partiële afgeleiden van de componenten van 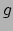 . We geven weer een
korte demonstratie voor poolcoördinaten.
. We geven weer een
korte demonstratie voor poolcoördinaten.
Voorbeeld: christoffelsymbolen en metriek
In poolcoördinaten geldt bijvoorbeeld
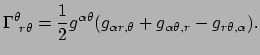 |
(298) |
Omdat
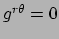 en
en
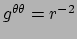 vinden we
vinden we
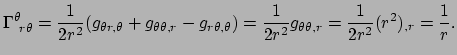 |
(299) |
Dit is hetzelfde resultaat voor
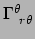 dat we al
eerder hebben afgeleid. Deze methode van berekenen is ook geldig in
gekromde ruimten.
dat we al
eerder hebben afgeleid. Deze methode van berekenen is ook geldig in
gekromde ruimten.




Next: De algemene relativiteitstheorie
Up: Christoffelsymbolen en de metriek
Previous: Christoffelsymbolen en de metriek
Contents
Jo van den Brand
2009-01-31
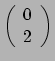 tensor. In cartesische
coördinaten zijn de componenten
tensor. In cartesische
coördinaten zijn de componenten
![]() te bepalen in termen
van
te bepalen in termen
van
![]() . Het omgekeerde blijkt ook waar te zijn:
. Het omgekeerde blijkt ook waar te zijn:
![]() uitdrukken in termen van
uitdrukken in termen van
![]() .
Dat geeft een eenvoudige manier om de christoffelsymbolen uit te rekenen.
We moeten eerst echter de relatie
.
Dat geeft een eenvoudige manier om de christoffelsymbolen uit te rekenen.
We moeten eerst echter de relatie
![]() bewijzen, die geldt in elk coördinatenstelsel.
Om deze symmetrie te bewijzen beschouwen we een willekeurig scalairveld
bewijzen, die geldt in elk coördinatenstelsel.
Om deze symmetrie te bewijzen beschouwen we een willekeurig scalairveld ![]() .
De eerste afgeleide
.
De eerste afgeleide
![]() is een 1-vorm met componenten
is een 1-vorm met componenten
![]() .
De tweede covariante afgeleide
.
De tweede covariante afgeleide
![]() heeft componenten
heeft componenten
![]() en is een
en is een
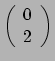 tensor. In cartesische
coördinaten zijn de componenten
tensor. In cartesische
coördinaten zijn de componenten