Een differentieerbare variëteit is een primitieve amorfe verzameling
van punten (puntgebeurtenissen voor het geval van ruimtetijd). Lokaal
zijn de punten gerangschikt als punten in een euclidische ruimte,
maar we hebben geen afstandsconcept gespecificeerd. Het is
absoluut cruciaal dat we een metriek ![]() toevoegen, die de informatie
bevat over hoe snel klokken lopen en wat de afstanden zijn tussen
punten.
toevoegen, die de informatie
bevat over hoe snel klokken lopen en wat de afstanden zijn tussen
punten.
Op het aardoppervlak zouden we een metriek bepalen door kleine
vectoren
![]() op het aardoppervlak te tekenen.
Vervolgens zeggen we dat de lengte van de vector gegeven wordt
door het inproduct
op het aardoppervlak te tekenen.
Vervolgens zeggen we dat de lengte van de vector gegeven wordt
door het inproduct
| (301) |
![$\displaystyle \vec A \cdot \vec B = {1 \over 4}\left[(\vec A + \vec B)^2
-(\vec A - \vec B)^2 \right] .$](img1379.png) |
(302) |
![\includegraphics[width=14cm]{Figures/llf.eps}](img1381.png)
|
We willen nu een metriek toekennen aan ruimtetijd. Hiertoe
introduceren we een lokaal lorentzframe (LLF). Dat doen we door
op punt
![]() in vrije val te gaan. Het equivalentieprincipe
zegt dan dat de effecten van gravitatie verdwijnen en dat we
lokaal de metriek van de speciale relativiteitstheorie vinden.
Dat is de minkowskimetriek. We kunnen op elk punt
in vrije val te gaan. Het equivalentieprincipe
zegt dan dat de effecten van gravitatie verdwijnen en dat we
lokaal de metriek van de speciale relativiteitstheorie vinden.
Dat is de minkowskimetriek. We kunnen op elk punt
![]() van de variëteit een coördinatenstelsel kiezen, waarin
de minkowskimetriek geldt. Terwijl dit in de SRT ook een globaal
coördinatenstelsel kan zijn, is dat enkel lokaal mogelijk in
de algemene relativiteitstheorie. Hiermee hebben we op elk
punt
van de variëteit een coördinatenstelsel kiezen, waarin
de minkowskimetriek geldt. Terwijl dit in de SRT ook een globaal
coördinatenstelsel kan zijn, is dat enkel lokaal mogelijk in
de algemene relativiteitstheorie. Hiermee hebben we op elk
punt
![]() een definitie van lengte gevonden: met
een definitie van lengte gevonden: met
![]() .
In essentie bedrijven we nu SRT op punt
.
In essentie bedrijven we nu SRT op punt
![]() en hebben we
een maat om lengten van staven en eigentijden van ideale
klokken te bepalen. In een LLF wordt de metriek gegeven door
en hebben we
een maat om lengten van staven en eigentijden van ideale
klokken te bepalen. In een LLF wordt de metriek gegeven door
![]() . Voor een riemannse variëteit
dienen alle diagonale elementen positief te zijn. De signatuur
(de som van de elementen op de diagonaal) van de metriek van
ruimtetijd is
. Voor een riemannse variëteit
dienen alle diagonale elementen positief te zijn. De signatuur
(de som van de elementen op de diagonaal) van de metriek van
ruimtetijd is ![]() , en we spreken van een pseudo-riemannse variëteit.
, en we spreken van een pseudo-riemannse variëteit.
Stel we brengen een coördinatenstelsel op het aardoppervlak
aan met longitude en lattitude.
Als we naar het oppervlak van de aarde kijken, dan zien we dat
hoe dichter je in de buurt van een punt
![]() blijft, hoe cartesischer
dit referentiesysteem er lokaal uit ziet. Afwijkingen van cartesische
coördinaten treden op in tweede orde in de afstand
blijft, hoe cartesischer
dit referentiesysteem er lokaal uit ziet. Afwijkingen van cartesische
coördinaten treden op in tweede orde in de afstand ![]() tot het
punt
tot het
punt
![]() . Wiskundig betekent dit dat geldt
. Wiskundig betekent dit dat geldt
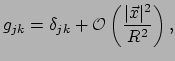 |
(303) |
Hetzelfde geldt voor ruimtetijd. In een gekromde ruimtetijd kunnen
we geen globaal lorentzframe vinden waarvoor
![]() .
Het is echter wel mogelijk om coördinaten te kiezen, zodat in
de nabijheid van
.
Het is echter wel mogelijk om coördinaten te kiezen, zodat in
de nabijheid van
![]() deze gelijkheid bijna geldig is.
Dat wordt mogelijk gemaakt door het equivalentieprincipe. Dit is
de precieze definitie van een lokaal lorentzframe en voor
een dergelijk coördinatenstelstel geldt
deze gelijkheid bijna geldig is.
Dat wordt mogelijk gemaakt door het equivalentieprincipe. Dit is
de precieze definitie van een lokaal lorentzframe en voor
een dergelijk coördinatenstelstel geldt
De metriek maakt het mogelijk om de lengte van een kromme te definiëren.
Als ![]() een kleine vectorverplaatsing op een curve is, dan is
de gekwadrateerde lengte gelijk aan
een kleine vectorverplaatsing op een curve is, dan is
de gekwadrateerde lengte gelijk aan
![]() (we noemen dit het lijnelement). Een maat voor de lengte wordt gevonden
door hiervan de absolute waarde te nemen en dan de wortel te
trekken. Dat geeft
(we noemen dit het lijnelement). Een maat voor de lengte wordt gevonden
door hiervan de absolute waarde te nemen en dan de wortel te
trekken. Dat geeft
![]() .
Integratie geeft dan de totale lengte en we vinden
.
Integratie geeft dan de totale lengte en we vinden
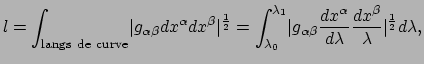 |
(305) |
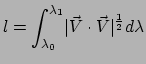 |
(306) |
Ook het berekenen van volumes is belangrijk als we integraties uitvoeren
in ruimtetijd. Met volume bedoelen we hier een vier-dimensionaal volume.
Stel we bevinden ons in een LLF en hebben er een volume element
![]() , met coördinaten
, met coördinaten
![]() in de lokale
lorentzmetriek
in de lokale
lorentzmetriek
![]() . Transformatietheorie zegt dan dat
. Transformatietheorie zegt dan dat
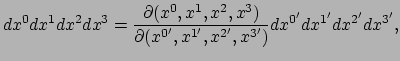 |
(307) |
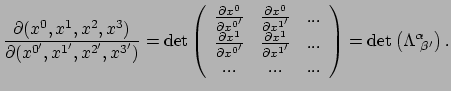 |
(308) |
| (309) |
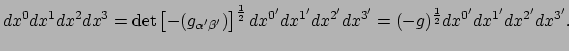 |
(310) |