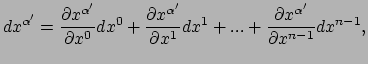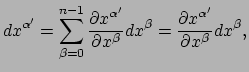Next: Geometrische objecten
Up: Wiskunde I - Differentiaaltopologie
Previous: Ruimtetijd van de ART
Contents
Coördinatentransformaties
Als we kijken naar Fig. 29, zien we dat om een punt
 van de variëteit te labelen, we een systeem van
van de variëteit te labelen, we een systeem van 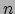 coördinaten gebruiken,
maar waarbij de keuze van de coördinaten arbitrair is. Het idee hierachter
is dat niet de `labels', maar de punten zelf, en de topologische en
geometrische relaties ertussen van belang zijn. We mogen punten herlabelen
door coördinatentransformaties uit te voeren,
coördinaten gebruiken,
maar waarbij de keuze van de coördinaten arbitrair is. Het idee hierachter
is dat niet de `labels', maar de punten zelf, en de topologische en
geometrische relaties ertussen van belang zijn. We mogen punten herlabelen
door coördinatentransformaties uit te voeren,
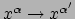 ,
uitgedrukt door
,
uitgedrukt door 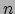 vergelijkingen
vergelijkingen
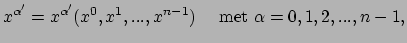 |
(81) |
waarbij we de nieuwe coördinaten geven als functie van de oude coördinaten.
Merk op dat we het accent aan de index hangen om de nieuwe coördinaten aan te geven.
We kunnen een coördinatentransformatie dus passief beschouwen als het
toekennen van nieuwe (geaccentueerde) coördinaten
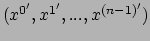 aan een punt van de variëteit, waarvan de oude coördinaten gegeven
worden door
aan een punt van de variëteit, waarvan de oude coördinaten gegeven
worden door
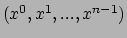 .
.
We zullen aannemen dat de functies gegeven in vergelijking (87)
eenwaardig, continu en differentieerbaar zijn over het valide bereik van hun
argumenten.
Door elke vergelijking in (87) te differentiëren naar
de oude coördinaten 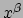 , krijgen we de
, krijgen we de
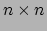 partiële afgeleiden
partiële afgeleiden
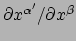 . Deze kunnen we samennemen in de
. Deze kunnen we samennemen in de
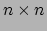 transformatiematrix
transformatiematrix
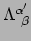
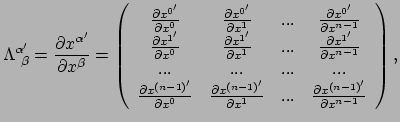 |
(82) |
zodat rijen worden gelabeld met een index in de teller van de partiële afgeleide
en kolommen door een index in de noemer. De elementen van de transformatiematrix
zijn functies van de coördinaten, en daarom zijn de numerieke waarden van de
matrixelementen in het algemeen verschillend als ze worden uitgerekend op
verschillende punten
 van de variëteit. De determinant van de
transformatiematrix wordt de jacobiaan van de transformatie genoemd en
wordt aangeduid met
van de variëteit. De determinant van de
transformatiematrix wordt de jacobiaan van de transformatie genoemd en
wordt aangeduid met
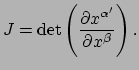 |
(83) |
Het is duidelijk dat de numerieke waarde van 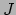 van punt tot punt in de variëteit
verandert.
van punt tot punt in de variëteit
verandert.
Stel dat 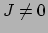 voor een bepaald bereik van de coördinaten
voor een bepaald bereik van de coördinaten 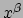 , dan betekent
dit dat we (in principe) vergelijkingen (87) kunnen oplossen
naar de oude coördinaten
, dan betekent
dit dat we (in principe) vergelijkingen (87) kunnen oplossen
naar de oude coördinaten 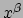 . We krijgen op deze wijze de inverse
transformatievergelijkingen
. We krijgen op deze wijze de inverse
transformatievergelijkingen
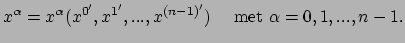 |
(84) |
Op dezelfde manier als hierboven kunnen we de inverse transformatiematrix
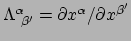 en de Jacobiaan van de inverse transformatie
en de Jacobiaan van de inverse transformatie
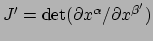 bepalen.
bepalen.
Als we de kettingregel gebruiken, dan kunnen we eenvoudig laten zien dat de
inverse transformatiematrix de inverse is van de transformatiematrix, omdat
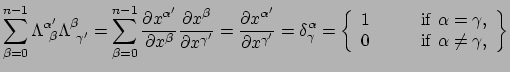 |
(85) |
waar we de Kronecker delta
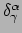 gebruiken, alsmede het feit dat
gebruiken, alsmede het feit dat
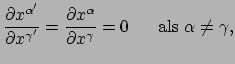 |
(86) |
omdat de coördinaten in zowel het geaccentueerde als in het
niet-geaccentueerde systeem onafhankelijk zijn. Omdat de twee
transformatiematrices elkaars inverse zijn, volgt
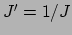 .
.
We beschouwen twee naburige punten
 en
en
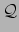 in de
variëteit, met respectievelijk coördinaten
in de
variëteit, met respectievelijk coördinaten 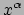 en
en
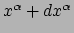 .
In het nieuwe systeem wordt de infinitesimale coördinatenafstand
tussen
.
In het nieuwe systeem wordt de infinitesimale coördinatenafstand
tussen
 en
en
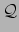 gegeven door de totale differentiaal
gegeven door de totale differentiaal
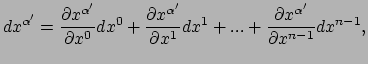 |
(87) |
waar we bedoelen dat de partiële afgeleiden aan de rechterzijde van
de vergelijking worden uitgerekend op punt
 . We kunnen
dit economischer schrijven als
. We kunnen
dit economischer schrijven als
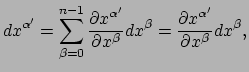 |
(88) |
waar we in de laatste stap de sommatieconventie van Einstein hebben ingevoerd.
Dit betekent dat als er in de uitdrukking dezelfde index boven als beneden voorkomt,
we automatisch sommeren over alle waarden die die index kan aannemen.




Next: Geometrische objecten
Up: Wiskunde I - Differentiaaltopologie
Previous: Ruimtetijd van de ART
Contents
Jo van den Brand
2009-01-31
![]() van de variëteit te labelen, we een systeem van
van de variëteit te labelen, we een systeem van ![]() coördinaten gebruiken,
maar waarbij de keuze van de coördinaten arbitrair is. Het idee hierachter
is dat niet de `labels', maar de punten zelf, en de topologische en
geometrische relaties ertussen van belang zijn. We mogen punten herlabelen
door coördinatentransformaties uit te voeren,
coördinaten gebruiken,
maar waarbij de keuze van de coördinaten arbitrair is. Het idee hierachter
is dat niet de `labels', maar de punten zelf, en de topologische en
geometrische relaties ertussen van belang zijn. We mogen punten herlabelen
door coördinatentransformaties uit te voeren,
![]() ,
uitgedrukt door
,
uitgedrukt door ![]() vergelijkingen
vergelijkingen
![]() , krijgen we de
, krijgen we de
![]() partiële afgeleiden
partiële afgeleiden
![]() . Deze kunnen we samennemen in de
. Deze kunnen we samennemen in de
![]() transformatiematrix
transformatiematrix
![]()
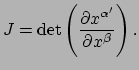
![]() voor een bepaald bereik van de coördinaten
voor een bepaald bereik van de coördinaten ![]() , dan betekent
dit dat we (in principe) vergelijkingen (87) kunnen oplossen
naar de oude coördinaten
, dan betekent
dit dat we (in principe) vergelijkingen (87) kunnen oplossen
naar de oude coördinaten ![]() . We krijgen op deze wijze de inverse
transformatievergelijkingen
. We krijgen op deze wijze de inverse
transformatievergelijkingen
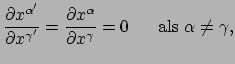
![]() en
en
![]() in de
variëteit, met respectievelijk coördinaten
in de
variëteit, met respectievelijk coördinaten ![]() en
en
![]() .
In het nieuwe systeem wordt de infinitesimale coördinatenafstand
tussen
.
In het nieuwe systeem wordt de infinitesimale coördinatenafstand
tussen
![]() en
en
![]() gegeven door de totale differentiaal
gegeven door de totale differentiaal