



Next: Coördinatentransformaties
Up: Wiskunde I - Differentiaaltopologie
Previous: Differentieerbare variëteit
Contents
We zullen nu plausibel proberen te maken dat ruimtetijd een
differentieerbare variëteit is. Daartoe wordt een geïdealiseerde
waarnemer ingevoerd, dat is een waarnemer met verwaarloosbare afmetingen
ten opzichte van de beschouwde schaal. Hierbij moet men denken aan
een massapunt met daarop een glad lopende klok. Deze klok hoeft voorlopig
helemaal niet eenparig (uniform) te lopen, als hij maar niet stilstaat.
Bij iedere puntgebeurtenis op de plaats van deze waarnemer (dus
op de plaats van het massapunt) hoort nu een eenduidig bepaald tijdstip,
namelijk de tijd 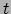 die de klok aanwijst als de puntgebeurtenis
die de klok aanwijst als de puntgebeurtenis
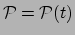 plaatsvindt. Voor een zeker tijdinterval
plaatsvindt. Voor een zeker tijdinterval
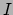 is er dus een bijectie
is er dus een bijectie
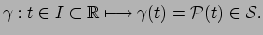 |
(80) |
Dit is een kromme in
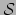 , de wereldlijn van de waarnemer. Er
zijn talloze voorbeelden van wereldlijnen te geven. Eén zo'n voorbeeld
is de wereldlijn van een punttrein, dat is een trein met verwaarloosbare
afmetingen ten opzichte van de beschouwde schaal (zie Fig. 31).
Hierin is
, de wereldlijn van de waarnemer. Er
zijn talloze voorbeelden van wereldlijnen te geven. Eén zo'n voorbeeld
is de wereldlijn van een punttrein, dat is een trein met verwaarloosbare
afmetingen ten opzichte van de beschouwde schaal (zie Fig. 31).
Hierin is 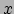 de afstand van de punttrein tot het station
de afstand van de punttrein tot het station 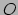 en
en 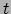 is de verlopen tijd sinds het vertrek uit
is de verlopen tijd sinds het vertrek uit 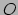 .
.
Figuur 31:
Wereldlijn van een punttrein. De vertikale delen van de wereldlijn
komen overeen met gebeurtenissen waarbij de trein stilstaat.
|
|
Lichtsignalen zijn van groot belang voor het beschrijven van de structuur
van ruimtetijd. Bij lichtsignalen moet men denken aan golfpakketjes van
radarsignalen, lichtpulsen of 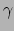 -quanta, waarvan de ruimtelijke
afmetingen en de tijdsduur weer verwaarloosbaar zijn ten opzichte van de
beschouwde schaal. Het is gebruikelijk doch niet geheel juist dergelijke
golfpakketjes collectief met de term foton aan te duiden. Het belang van
fotonen met betrekking tot de structuur van ruimtetijd is te wijten aan de
empirisch vastgestelde universaliteit van de voorplanting van elektromagnetische
golven in vacuüm, dat wil zeggen de voortplantingssnelheid in vacuüm is
onafhankelijk van de bewegingstoestand van de bron en van de golflengte,
de intensiteit en de polarisatie van de elektromagnetische golven.
-quanta, waarvan de ruimtelijke
afmetingen en de tijdsduur weer verwaarloosbaar zijn ten opzichte van de
beschouwde schaal. Het is gebruikelijk doch niet geheel juist dergelijke
golfpakketjes collectief met de term foton aan te duiden. Het belang van
fotonen met betrekking tot de structuur van ruimtetijd is te wijten aan de
empirisch vastgestelde universaliteit van de voorplanting van elektromagnetische
golven in vacuüm, dat wil zeggen de voortplantingssnelheid in vacuüm is
onafhankelijk van de bewegingstoestand van de bron en van de golflengte,
de intensiteit en de polarisatie van de elektromagnetische golven.
Beschouw nu een radarstation 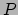 , dat een puntgebeurtenis
, dat een puntgebeurtenis 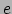 waarneemt.
Het radarstation is klein genoeg om dit met een wereldlijn in
waarneemt.
Het radarstation is klein genoeg om dit met een wereldlijn in
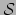 te beschrijven. Bij de puntgebeurtenis
te beschrijven. Bij de puntgebeurtenis 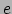 kan men denken aan een vliegtuig
waaraan op een zeker tijdstip en op een zekere plaats het radarsignaal
wordt gereflecteerd. De tijd
kan men denken aan een vliegtuig
waaraan op een zeker tijdstip en op een zekere plaats het radarsignaal
wordt gereflecteerd. De tijd 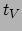 van vertrek van het radarsignaal en
de tijd
van vertrek van het radarsignaal en
de tijd 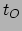 van ontvangst van het gereflecteerde radarsignaal worden
door het radarstation
van ontvangst van het gereflecteerde radarsignaal worden
door het radarstation 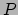 geregistreerd. In de newtonse mechanica wordt een
puntgebeurtenis vastgelegd door vier coördinaten,
geregistreerd. In de newtonse mechanica wordt een
puntgebeurtenis vastgelegd door vier coördinaten,
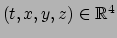 .
Daarom introduceren we een tweede radarstation
.
Daarom introduceren we een tweede radarstation 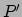 , dat een andere
wereldlijn beschrijft en tijden
, dat een andere
wereldlijn beschrijft en tijden
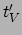 en
en
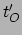 registreert
voor dezelfde puntgebeurtenis
registreert
voor dezelfde puntgebeurtenis 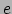 met de klok op
met de klok op 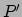 . Men veronderstelt
nu dat er een deelverzameling
. Men veronderstelt
nu dat er een deelverzameling 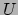 van
van
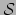 bestaat, zodanig dat
voor iedere puntgebeurtenis uit
bestaat, zodanig dat
voor iedere puntgebeurtenis uit 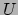 de vier reële getallen
de vier reële getallen
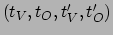 een coördinatenstelsel vormen.
De kaart
een coördinatenstelsel vormen.
De kaart
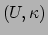 met
met
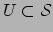 en
en
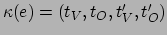 heet een
radarcoördinatenstelsel. Er is hier ondersteld dat een radarstation
door slechts één uitgaande en één terugkomende radarpuls met
heet een
radarcoördinatenstelsel. Er is hier ondersteld dat een radarstation
door slechts één uitgaande en één terugkomende radarpuls met 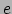 verbonden is. Als het heelal gesloten is zou puntgebeurtenis
verbonden is. Als het heelal gesloten is zou puntgebeurtenis 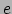 door meer
dan twee radarsignalen met een radarstation verbonden kunnen zijn. We
beperken daarom in bovenstaande constructie alle wereldlijnen tot een
deelverzameling
door meer
dan twee radarsignalen met een radarstation verbonden kunnen zijn. We
beperken daarom in bovenstaande constructie alle wereldlijnen tot een
deelverzameling 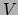 van
van
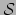 , zodat
, zodat 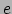 en
en 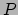 , respectievelijk
, respectievelijk
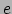 en
en 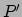 door slechts twee radarpulsen worden verbonden.
Dit wordt schematisch weergegeven in Fig. 32.
door slechts twee radarpulsen worden verbonden.
Dit wordt schematisch weergegeven in Fig. 32.
Figuur 32:
Twee waarnemers brengen een gebeurtenis in kaart door er
radarpulsen aan te reflecteren. Radarcoördinaten van een puntgebeurtenis 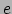 worden gevormd door tijden van vertrek en ontvangst van deze radarpulsen.
worden gevormd door tijden van vertrek en ontvangst van deze radarpulsen.
|
|
Door nu ruimtetijd
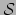 lapjesgewijs helemaal in kaart te brengen
op bovenstaande wijze komt men tot de uitspraak: ruimtetijd is
een vierdimensionale differentieerbare variëteit.
lapjesgewijs helemaal in kaart te brengen
op bovenstaande wijze komt men tot de uitspraak: ruimtetijd is
een vierdimensionale differentieerbare variëteit.
Er zijn naast genoemde manier nog andere manieren om ruimtetijd van
coördinaten te voorzien. We noemen er twee.
- Breng in ruimtetijd een voldoend dichte zwerm willekeurig
bewegende deeltjes aan (massapunten), en voorzie ieder van deze
deeltjes van een klok die weer niet noodzakelijkerwijs eenparig
hoeft te lopen, als hij maar niet stilstaat. Kenmerk verder ieder
deeltje door drie reële getallen
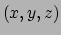 om ze van elkaar te
onderscheiden. Aan een puntgebeurtenis worden nu vier reële
getallen toegevoegd, namelijk het drietal plaatscoördinaten
om ze van elkaar te
onderscheiden. Aan een puntgebeurtenis worden nu vier reële
getallen toegevoegd, namelijk het drietal plaatscoördinaten
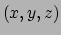 van het massapunt
van het massapunt 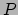 waar de puntgebeurtenis
waar de puntgebeurtenis 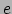 plaatsvindt
en het tijdstip
plaatsvindt
en het tijdstip 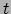 dat de klok van
dat de klok van 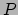 aanwijst op het moment
dat de puntgebeurtenis
aanwijst op het moment
dat de puntgebeurtenis 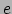 wordt waargenomen. We krijgen zo een
kaart
wordt waargenomen. We krijgen zo een
kaart
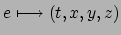 . Het coördinatenstelsel wordt
zo geconstrueerd dat voor naburige puntgebeurtenissen bijbehorende
. Het coördinatenstelsel wordt
zo geconstrueerd dat voor naburige puntgebeurtenissen bijbehorende
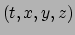 weinig verschillen.
weinig verschillen.
- Neem vier waarnemers met ieder een lopende klok, die
willekeurig bewegen. Laat deze waarnemers de aankomsttijden
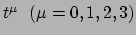 van een lichtsignaal registreren dat door een
puntgebeurtenis
van een lichtsignaal registreren dat door een
puntgebeurtenis 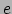 is uitgezonden. Men krijgt voor de puntgebeurtenis
is uitgezonden. Men krijgt voor de puntgebeurtenis
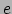 dan vier coördinaten
dan vier coördinaten 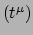 .
.
De belangrijkste begrippen met betrekking tot de structuur van ruimtetijd
zijn dus puntgebeurtenis, massapunt, foton en klok.




Next: Coördinatentransformaties
Up: Wiskunde I - Differentiaaltopologie
Previous: Differentieerbare variëteit
Contents
Jo van den Brand
2009-01-31
![]() die de klok aanwijst als de puntgebeurtenis
die de klok aanwijst als de puntgebeurtenis
![]() plaatsvindt. Voor een zeker tijdinterval
plaatsvindt. Voor een zeker tijdinterval
![]() is er dus een bijectie
is er dus een bijectie
![\includegraphics[width=8cm]{Figures/punttrein.eps}](img589.png)
![]() , dat een puntgebeurtenis
, dat een puntgebeurtenis ![]() waarneemt.
Het radarstation is klein genoeg om dit met een wereldlijn in
waarneemt.
Het radarstation is klein genoeg om dit met een wereldlijn in
![]() te beschrijven. Bij de puntgebeurtenis
te beschrijven. Bij de puntgebeurtenis ![]() kan men denken aan een vliegtuig
waaraan op een zeker tijdstip en op een zekere plaats het radarsignaal
wordt gereflecteerd. De tijd
kan men denken aan een vliegtuig
waaraan op een zeker tijdstip en op een zekere plaats het radarsignaal
wordt gereflecteerd. De tijd ![]() van vertrek van het radarsignaal en
de tijd
van vertrek van het radarsignaal en
de tijd ![]() van ontvangst van het gereflecteerde radarsignaal worden
door het radarstation
van ontvangst van het gereflecteerde radarsignaal worden
door het radarstation ![]() geregistreerd. In de newtonse mechanica wordt een
puntgebeurtenis vastgelegd door vier coördinaten,
geregistreerd. In de newtonse mechanica wordt een
puntgebeurtenis vastgelegd door vier coördinaten,
![]() .
Daarom introduceren we een tweede radarstation
.
Daarom introduceren we een tweede radarstation ![]() , dat een andere
wereldlijn beschrijft en tijden
, dat een andere
wereldlijn beschrijft en tijden
![]() en
en
![]() registreert
voor dezelfde puntgebeurtenis
registreert
voor dezelfde puntgebeurtenis ![]() met de klok op
met de klok op ![]() . Men veronderstelt
nu dat er een deelverzameling
. Men veronderstelt
nu dat er een deelverzameling ![]() van
van
![]() bestaat, zodanig dat
voor iedere puntgebeurtenis uit
bestaat, zodanig dat
voor iedere puntgebeurtenis uit ![]() de vier reële getallen
de vier reële getallen
![]() een coördinatenstelsel vormen.
De kaart
een coördinatenstelsel vormen.
De kaart
![]() met
met
![]() en
en
![]() heet een
radarcoördinatenstelsel. Er is hier ondersteld dat een radarstation
door slechts één uitgaande en één terugkomende radarpuls met
heet een
radarcoördinatenstelsel. Er is hier ondersteld dat een radarstation
door slechts één uitgaande en één terugkomende radarpuls met ![]() verbonden is. Als het heelal gesloten is zou puntgebeurtenis
verbonden is. Als het heelal gesloten is zou puntgebeurtenis ![]() door meer
dan twee radarsignalen met een radarstation verbonden kunnen zijn. We
beperken daarom in bovenstaande constructie alle wereldlijnen tot een
deelverzameling
door meer
dan twee radarsignalen met een radarstation verbonden kunnen zijn. We
beperken daarom in bovenstaande constructie alle wereldlijnen tot een
deelverzameling ![]() van
van
![]() , zodat
, zodat ![]() en
en ![]() , respectievelijk
, respectievelijk
![]() en
en ![]() door slechts twee radarpulsen worden verbonden.
Dit wordt schematisch weergegeven in Fig. 32.
door slechts twee radarpulsen worden verbonden.
Dit wordt schematisch weergegeven in Fig. 32.
![\includegraphics[width=12cm]{Figures/radar.eps}](img598.png)