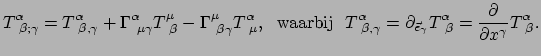Next: Geodeten en kromming
Up: De algemene relativiteitstheorie
Previous: Pseudo-riemannse variëteit
Contents
Stel we hebben een tensorveld
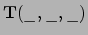 met rang 3. Dit veld
is een functie van lokatie en definieert een tensor op elk punt
met rang 3. Dit veld
is een functie van lokatie en definieert een tensor op elk punt
 .
We kunnen deze tensor expanderen in de basis
.
We kunnen deze tensor expanderen in de basis
 en dat
geeft de (boven-) componenten
en dat
geeft de (boven-) componenten
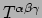 . In het algemeen
hebben we 64 termen voor ruimtetijd. We kunnen de tensor
. In het algemeen
hebben we 64 termen voor ruimtetijd. We kunnen de tensor 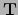 echter ook
expanderen in de duale basis
echter ook
expanderen in de duale basis
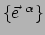 en er geldt
en er geldt
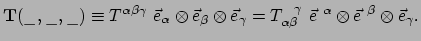 |
(311) |
Als je de waarden van de componenten wilt berekenen dan wordt het volgende
theorema gebruikt,
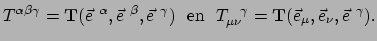 |
(312) |
Als je de componenten van de tensor 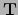 in een of andere rangschikking
van boven- en benedenindices hebt, en je wilt de componenten weten in een
andere rangschikking van indices, dan wordt de metriek gebruikt. Er geldt
in een of andere rangschikking
van boven- en benedenindices hebt, en je wilt de componenten weten in een
andere rangschikking van indices, dan wordt de metriek gebruikt. Er geldt
 |
(313) |
Vervolgens willen we contractie bespreken. Dat is nogal ingewikkeld om te
behandelen in onze abstracte notatie. Gegeven een tensor 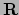 , kunnen
we deze altijd schrijven in termen van een basis van vectoren als
, kunnen
we deze altijd schrijven in termen van een basis van vectoren als
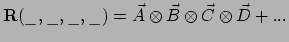 |
(314) |
We bespreken contractie enkel voor een tensorproduct van vectoren en gebruiken
lineariteit om een wiskundige beschrijving voor algemene tensoren te vinden.
Voor contractie
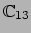 van de eerste met de derde index geldt
van de eerste met de derde index geldt
![$\displaystyle \mathbb{C}_{13} \left[
\vec A \otimes \vec B \otimes \vec C \oti...
..._,\_,\_) \right]
\equiv ( \vec A \cdot \vec C) \vec B \otimes \vec D (\_,\_) .$](img1421.png) |
(315) |
We kunnen bovenstaande abstracte definitie in termen van componenten schrijven
en vinden
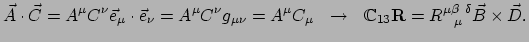 |
(316) |
Op dezelfde manier als hierboven, zien we
dat we uit twee vectoren 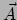 en
en 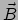 een tensor
een tensor
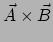 kunnen construeren door er het tensorproduct van te nemen,
terwijl we een scalar
kunnen construeren door er het tensorproduct van te nemen,
terwijl we een scalar
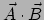 kunnen maken door het inproduct te nemen.
De contractie van het tensorproduct
kunnen maken door het inproduct te nemen.
De contractie van het tensorproduct
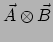 levert weer een scalar op,
levert weer een scalar op,
![$ \mathbb{C}\left[ \vec A \otimes \vec B \right] = \vec A \cdot \vec B$](img1426.png) .
.
Vanaf nu gaan we een vergelijking als
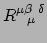 vanuit een
ander gezichtspunt bekijken. We hebben het steeds gezien als de
componenten van een tensor. Vanaf nu is onze interpretatie dat de indices
vanuit een
ander gezichtspunt bekijken. We hebben het steeds gezien als de
componenten van een tensor. Vanaf nu is onze interpretatie dat de indices
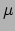 ,
, 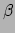 ,
, 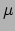 en
en 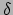 labels zijn van de sleuven van de
abstracte tensor
labels zijn van de sleuven van de
abstracte tensor 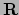 . Dus met
. Dus met
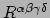 bedoelen we
de abstracte tensor
bedoelen we
de abstracte tensor
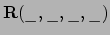 met eerste sleuf
met eerste sleuf 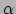 ,
tweede sleuf
,
tweede sleuf 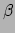 , enz.
, enz.
Het bovenstaande rondt onze discussie over tensoralgebra af. In het volgende
gaan we tensoranalyse bespreken. Dit doen we aan de hand van een
tensorveld
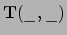 met rang 2, maar wat we concluderen is
geldig voor elk tensorveld. Het veld
met rang 2, maar wat we concluderen is
geldig voor elk tensorveld. Het veld 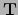 is een functie van lokatie in de variëteit,
is een functie van lokatie in de variëteit,
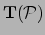 .
We differentiëren
.
We differentiëren 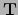 nu langs de curve
nu langs de curve
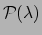 .
Op punt
.
Op punt
 wordt de raakvector
wordt de raakvector 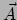 aan de curve
gegeven door
aan de curve
gegeven door
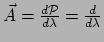 .
De afgeleide van
.
De afgeleide van 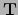 langs de curve (dus in de richting van
vector
langs de curve (dus in de richting van
vector 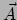 ) wordt gegeven door
) wordt gegeven door
![$\displaystyle \nabla_{\vec A} {\bf T} = \lim_{\Delta \lambda \rightarrow 0}
{...
...da ))\right]^\parallel
-{\bf T}(\mathcal{P}(\lambda )) \over \Delta \lambda }.$](img1434.png) |
(317) |
Merk op dat de twee tensoren,
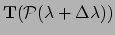 en
en
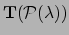 , in twee verschillende raakruimten
leven. Ze zijn bijna hetzelfde, omdat
, in twee verschillende raakruimten
leven. Ze zijn bijna hetzelfde, omdat
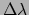 klein is, maar
desalniettemin zijn het verschillende raakruimten. We hebben een manier
nodig om de tensor
klein is, maar
desalniettemin zijn het verschillende raakruimten. We hebben een manier
nodig om de tensor
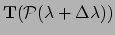 naar
punt
naar
punt
 te transporteren, waar we de afgeleide willen bepalen,
zodat we de tensoren kunnen aftrekken. Wat we nodig hebben wordt
parallel transporteren van
te transporteren, waar we de afgeleide willen bepalen,
zodat we de tensoren kunnen aftrekken. Wat we nodig hebben wordt
parallel transporteren van
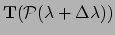 genoemd.
genoemd.
In een gekromde variëteit zien we de effecten van kromming niet als we
eerste-orde afgeleiden nemen65.
Het parallel transporteren betekent dan
hetzelfde als wat het betekent in een vlakke ruimte: de componenten
veranderen niet door het transporteren. We hebben dus met vergelijking
(323) een uitdrukking voor de afgeleide gevonden. De
orgininele tensor
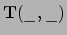 heeft twee sleuven, en dat is ook
zo voor de afgeleide
heeft twee sleuven, en dat is ook
zo voor de afgeleide
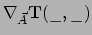 , want volgens
vergelijking (323) is de afgeleide niets anders dan het
verschil van twee tensoren
, want volgens
vergelijking (323) is de afgeleide niets anders dan het
verschil van twee tensoren 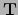 op verschillende punten, en dan
gedeeld door de afstand
op verschillende punten, en dan
gedeeld door de afstand
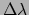 .
.
Als volgende stap kunnen we nu het concept gradiënt invoeren. We merken op
dat de afgeleide
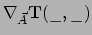 lineair is in de
vector
lineair is in de
vector 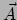 . Dat betekent dat er een rang-3 tensor
. Dat betekent dat er een rang-3 tensor
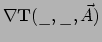 bestaat, zodanig, dat geldt
bestaat, zodanig, dat geldt
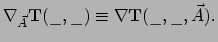 |
(319) |
Dit is de definitie van de gradiënt van 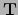 .
Het laatste slot wordt per conventie gebruikt als het differentiatieslot.
De gradiënt van
.
Het laatste slot wordt per conventie gebruikt als het differentiatieslot.
De gradiënt van 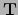 is een lineaire functie van vectoren en
heeft één sleuf meer dan
is een lineaire functie van vectoren en
heeft één sleuf meer dan 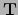 zelf, en heeft verder de eigenschap dat als
je
zelf, en heeft verder de eigenschap dat als
je 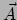 in de laatste sleuf stopt, je de afgeleide van
in de laatste sleuf stopt, je de afgeleide van 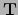 krijgt in de richting van
krijgt in de richting van 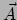 . We definiëren de componenten van
de gradiënt als
. We definiëren de componenten van
de gradiënt als
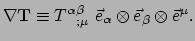 |
(320) |
Het is een conventie om de differentiatie index beneden te plaatsen.
Merk verder op dat je deze differentiatie index naar boven of beneden
kunt halen net als elke andere index. Verder correspondeert alles dat na de puntkomma
komt met een gradiënt. De componenten van de gradiënt zijn in
dit geval
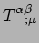 .
.
Hoe berekenen we de componenten van een gradiënt? Het gereedschap
hiervoor zijn de zogenaamde connectie coëfficiënten66.
Die coëfficiënten worden zo genoemd, omdat bij het nemen van
de afgeleide we het tensorveld in twee verschillende raakruimten
moeten vergelijken. De connectie coëfficiënten geven ons
informatie over hoe de basisvectoren veranderen tussen beide
naburige raakruimten. Omdat we
een basis hebben in punt
 ,
kunnen we ons afvragen wat de afgeleide is van
,
kunnen we ons afvragen wat de afgeleide is van
 in de richting van
in de richting van
 . Er geldt
. Er geldt
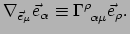 |
(321) |
Deze afgeleide is zelf ook een vector en we kunnen deze dus expanderen
in onze basis op punt
 waar we de afgeleide willen weten.
De expansiecoëfficiënten zijn
waar we de afgeleide willen weten.
De expansiecoëfficiënten zijn
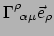 .
Evenzo geldt
.
Evenzo geldt
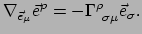 |
(322) |
Merk op dat we nu een minteken krijgen!
De connectie coëfficiënten
vertellen je hoe de basisvectoren van plaats tot plaats veranderen. Dus als
je de componenten van een gradiënt wilt weten, bijvoorbeeld
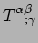 , dan moet je correcties maken voor het feit
dat de basisvectoren veranderen. De tensor
, dan moet je correcties maken voor het feit
dat de basisvectoren veranderen. De tensor
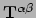 is
zelf misschien constant en enkel de basisvectoren hangen van positie af.
Het blijkt dat (zie ook vergelijking (285))
is
zelf misschien constant en enkel de basisvectoren hangen van positie af.
Het blijkt dat (zie ook vergelijking (285))
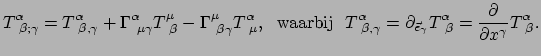 |
(323) |
Als we de metriek 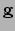 kennen, dan kunnen we de christoffelsymbolen
uitrekenen, en daarmee alle covariante afgeleiden. Hiermee vinden we
tenslotte weer de vergelijkingen
kennen, dan kunnen we de christoffelsymbolen
uitrekenen, en daarmee alle covariante afgeleiden. Hiermee vinden we
tenslotte weer de vergelijkingen




Next: Geodeten en kromming
Up: De algemene relativiteitstheorie
Previous: Pseudo-riemannse variëteit
Contents
Jo van den Brand
2009-01-31
![]() met rang 3. Dit veld
is een functie van lokatie en definieert een tensor op elk punt
met rang 3. Dit veld
is een functie van lokatie en definieert een tensor op elk punt
![]() .
We kunnen deze tensor expanderen in de basis
.
We kunnen deze tensor expanderen in de basis
![]() en dat
geeft de (boven-) componenten
en dat
geeft de (boven-) componenten
![]() . In het algemeen
hebben we 64 termen voor ruimtetijd. We kunnen de tensor
. In het algemeen
hebben we 64 termen voor ruimtetijd. We kunnen de tensor ![]() echter ook
expanderen in de duale basis
echter ook
expanderen in de duale basis
![]() en er geldt
en er geldt
![]() , kunnen
we deze altijd schrijven in termen van een basis van vectoren als
, kunnen
we deze altijd schrijven in termen van een basis van vectoren als
![]() vanuit een
ander gezichtspunt bekijken. We hebben het steeds gezien als de
componenten van een tensor. Vanaf nu is onze interpretatie dat de indices
vanuit een
ander gezichtspunt bekijken. We hebben het steeds gezien als de
componenten van een tensor. Vanaf nu is onze interpretatie dat de indices
![]() ,
, ![]() ,
, ![]() en
en ![]() labels zijn van de sleuven van de
abstracte tensor
labels zijn van de sleuven van de
abstracte tensor ![]() . Dus met
. Dus met
![]() bedoelen we
de abstracte tensor
bedoelen we
de abstracte tensor
![]() met eerste sleuf
met eerste sleuf ![]() ,
tweede sleuf
,
tweede sleuf ![]() , enz.
, enz.
![]() met rang 2, maar wat we concluderen is
geldig voor elk tensorveld. Het veld
met rang 2, maar wat we concluderen is
geldig voor elk tensorveld. Het veld ![]() is een functie van lokatie in de variëteit,
is een functie van lokatie in de variëteit,
![]() .
We differentiëren
.
We differentiëren ![]() nu langs de curve
nu langs de curve
![]() .
Op punt
.
Op punt
![]() wordt de raakvector
wordt de raakvector ![]() aan de curve
gegeven door
aan de curve
gegeven door
![]() .
De afgeleide van
.
De afgeleide van ![]() langs de curve (dus in de richting van
vector
langs de curve (dus in de richting van
vector ![]() ) wordt gegeven door
) wordt gegeven door
![]() heeft twee sleuven, en dat is ook
zo voor de afgeleide
heeft twee sleuven, en dat is ook
zo voor de afgeleide
![]() , want volgens
vergelijking (323) is de afgeleide niets anders dan het
verschil van twee tensoren
, want volgens
vergelijking (323) is de afgeleide niets anders dan het
verschil van twee tensoren ![]() op verschillende punten, en dan
gedeeld door de afstand
op verschillende punten, en dan
gedeeld door de afstand
![]() .
.
![]() lineair is in de
vector
lineair is in de
vector ![]() . Dat betekent dat er een rang-3 tensor
. Dat betekent dat er een rang-3 tensor
![]() bestaat, zodanig, dat geldt
bestaat, zodanig, dat geldt
![]() ,
kunnen we ons afvragen wat de afgeleide is van
,
kunnen we ons afvragen wat de afgeleide is van
![]() in de richting van
in de richting van
![]() . Er geldt
. Er geldt