![\includegraphics[width=8cm]{Figures/pt.eps}](img1457.png)
|
Als we sferische coördinaten aanbrengen op een bol, en we volgen twee lijnen, die loodrecht op de evenaar staan, in richting van de noordpool, dan zien we dat de initieel parallelle lijnen een snijpunt hebben op het gekromde oppervlak. Het vijfde postulaat van Euclides geldt dus niet in een gekromde ruimte: parallelle lijnen kunnen wel degelijk een snijpunt hebben.
![\includegraphics[width=8cm]{Figures/pt.eps}](img1457.png)
|
Een andere illustratie van hoe kromming zich manifesteert, en die misschien
nog doeltreffender is, wordt gegeven in Fig. 47.
We beginnen in punt P met een raakvector die in de horizontale
richting wijst. We nemen een kleine stap in de richting van Q en
na elke step projecteren we de raakvector weer op het lokale
raakvlak. Dit is onze manier van parallel transporteren. Nadat we
het gesloten traject PQRP hebben volbracht, zien we dat de eindvector
niet meer parallel is aan de initiële vector. Dit gebeurt niet
in een vlakke ruimte is een effect van de kromming van de bol.
De consequentie is dat we op een gekromde variëteit geen
globale parallelle vectorvelden kunnen definiëren. Het resultaat
van parallel transporteren hangt af van de gekozen weg en van de
grootte van de lus.
Teneinde een wiskundige beschrijving te vinden, vatten we het interval
PQ in Fig. 47 op als een curve, en stellen we dat ![]() de
parameter is van deze curve. Het vectorveld
de
parameter is van deze curve. Het vectorveld ![]() is gedefinieerd
op elk punt van de curve. De vector
is gedefinieerd
op elk punt van de curve. De vector
![]() is
de raakvector aan de curve. In een lokaal coördinatensysteem
op punt
is
de raakvector aan de curve. In een lokaal coördinatensysteem
op punt
![]() moeten de componenten van
moeten de componenten van ![]() constant zijn langs de curve, er geldt
constant zijn langs de curve, er geldt
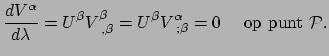 |
(325) |
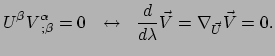 |
(326) |
De belangrijkste curven in een gekromde ruimte zijn de geodeten.
Geodeten zijn lijnen die (zo recht als mogelijk is) zijn getrokken, met
als voorwaarde dat de raakvectoren ![]() van deze lijnen parallel getransporteerd
worden. Voor een geodeet geldt dus
van deze lijnen parallel getransporteerd
worden. Voor een geodeet geldt dus
| (328) |
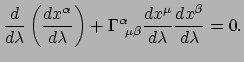 |
(329) |
Door de parameter ![]() te veranderen, veranderen we wiskundig de
curve (maar niet het pad). Als
te veranderen, veranderen we wiskundig de
curve (maar niet het pad). Als ![]() een parameter van de geodeet is,
en we definiëren een nieuwe parameter
een parameter van de geodeet is,
en we definiëren een nieuwe parameter
![]() , met
, met ![]() en
en ![]() constanten, die dus niet van de positie op de curve afhangen, dan
geldt voor
constanten, die dus niet van de positie op de curve afhangen, dan
geldt voor ![]() ook
ook
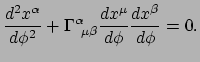 |
(330) |