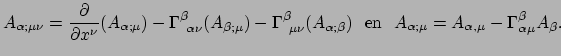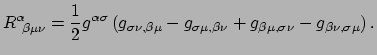Next: Newtoniaanse beschrijving van getijdenkrachten
Up: De algemene relativiteitstheorie
Previous: Geodeten en kromming
Contents
In Fig. 48 tonen we twee vectorenvelden 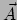 en
en 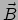 .
De vectoren zijn zo klein, dat de kromming van de variëteit geen rol
speelt in het gebied waar dit diagram getekend is. We kunnen daarmee
aannemen dat de vectoren op het oppervlak liggen in plaats van in de
raakruimte. Teneinde de commutator
.
De vectoren zijn zo klein, dat de kromming van de variëteit geen rol
speelt in het gebied waar dit diagram getekend is. We kunnen daarmee
aannemen dat de vectoren op het oppervlak liggen in plaats van in de
raakruimte. Teneinde de commutator
![$ [\vec A, \vec B]$](img1475.png) uit te kunnen rekenen,
gebruiken we een lokaal orthonormaal coördinatensysteem. Omdat we
een vector kunnen opvatten als een richtingsafgeleide, stelt
uit te kunnen rekenen,
gebruiken we een lokaal orthonormaal coördinatensysteem. Omdat we
een vector kunnen opvatten als een richtingsafgeleide, stelt
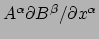 de grootte voor waarmee de
vector
de grootte voor waarmee de
vector 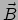 verandert als die langs
verandert als die langs 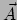 verplaatst wordt (dat
is de korte gestreepte lijn rechtsboven in Fig 48).
verplaatst wordt (dat
is de korte gestreepte lijn rechtsboven in Fig 48).
Figuur:
De commutator
![$ [\vec A, \vec B]$](img1475.png) van twee vectorvelden. We nemen
aan dat de vectoren klein zijn, zodat de kromming het toelaat dat ze in
de variëteit liggen.
van twee vectorvelden. We nemen
aan dat de vectoren klein zijn, zodat de kromming het toelaat dat ze in
de variëteit liggen.
|
|
Evenzo is
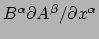 de verandering
van
de verandering
van 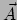 als die langs
als die langs 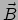 verplaatst wordt (dat is die andere
korte gestreepte lijn). Voor de componenten van de commutator in een
coördinatenstelsel geldt
verplaatst wordt (dat is die andere
korte gestreepte lijn). Voor de componenten van de commutator in een
coördinatenstelsel geldt
![$\displaystyle [ \vec A, \vec B ] = \left[ A^\alpha {\partial \over \partial x^\...
...l A^\beta \over \partial x^\alpha} \right)
{\partial \over \partial x^\beta} .$](img1479.png) |
(331) |
Volgens bovenstaande vergelijking is de commutator
![$ [\vec A, \vec B]$](img1475.png) het
verschil van de twee gestreepte lijnen in Fig. 48. Het is
het vijfde lijnsegment dat nodig is om de vierhoek te sluiten (dat is
de geometrische betekenis van de commutator). Vergelijking
(337) is een operatorvergelijking, waarbij de uiteindelijke
afgeleide opereert op een scalairveld (net als in de quantummechanica).
We vinden hiermee meteen de componenten van de commutator in een
willekeurig coördinatenstelsel:
het
verschil van de twee gestreepte lijnen in Fig. 48. Het is
het vijfde lijnsegment dat nodig is om de vierhoek te sluiten (dat is
de geometrische betekenis van de commutator). Vergelijking
(337) is een operatorvergelijking, waarbij de uiteindelijke
afgeleide opereert op een scalairveld (net als in de quantummechanica).
We vinden hiermee meteen de componenten van de commutator in een
willekeurig coördinatenstelsel:
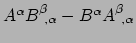 . De
commutator is nuttig om onderscheid te kunnen maken tussen een
coördinatenbasis en een niet-coördinatenbasis (ook wel niet-holonomische
basis genoemd)67.
. De
commutator is nuttig om onderscheid te kunnen maken tussen een
coördinatenbasis en een niet-coördinatenbasis (ook wel niet-holonomische
basis genoemd)67.
In de discussie die leidde tot vergelijking (310), zagen we
dat de effecten van kromming merkbaar worden als we tweede-orde
afgeleiden (of gradiënten) nemen van de metriek.
De krommingstensor van Riemann is een maat voor het falen van dubbele
gradiënten om te sluiten. Neem een vectorveld 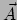 en neem er de
dubbele gradiënten van. Dan vinden we
en neem er de
dubbele gradiënten van. Dan vinden we
![$\displaystyle A_{\alpha ; \mu \nu} - A_{\alpha ; \nu \mu}
=[ \nabla_\mu , \nabla_\nu ] A_\alpha \equiv
R_{~\alpha \mu \nu}^\beta A_{\beta} .$](img1485.png) |
(332) |
Deze vergelijking kan gezien worden als de definitie van de
riemanntensor. We kunnen deze vergelijking uitwerken door te beginnen
met de definitie van de covariante afgeleide,
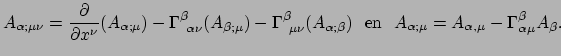 |
(333) |
We dienen nu een en ander te differentiëren, indices te manipuleren, etc.
Uiteindelijk vinden we
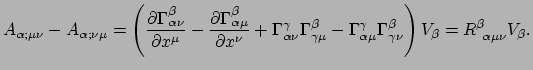 |
(334) |
De riemanntensor vertelt ons hoe een vectorveld verandert langs
een gesloten pad. We kunnen vergelijking (324) gebruiken om
de riemanntensor in een LLF te schrijven als
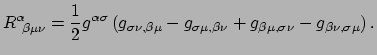 |
(335) |
We zien dat de metrische tensor 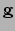 de informatie over de
intrinsieke kromming bevat68.
Deze kromming wordt manifest als we tweede-orde
afgeleiden van de metriek nemen.
Met
de informatie over de
intrinsieke kromming bevat68.
Deze kromming wordt manifest als we tweede-orde
afgeleiden van de metriek nemen.
Met
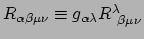 en bovenstaande relatie,
kunnen we een aantal belangrijke eigenschappen van de riemanntensor bewijzen.
De riemanntensor is
en bovenstaande relatie,
kunnen we een aantal belangrijke eigenschappen van de riemanntensor bewijzen.
De riemanntensor is
- antisymmetrisch in de laatste twee indices. Er geldt
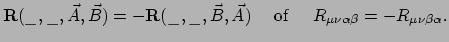 |
(336) |
- Antisymmetrisch in de eerste twee indices. Er geldt
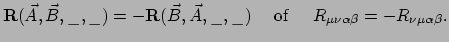 |
(337) |
- De tensor is symmetrisch.
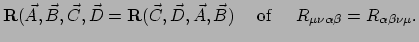 |
(338) |
- Er gelden de zogenaamde Biancchi identiteiten,
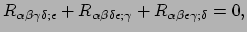 |
(339) |
waarbij we steeds de laatste drie indices permuteren.
Bovenstaande symmetriën reduceren de
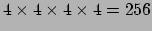 componenten van de riemanntensor tot 20.
componenten van de riemanntensor tot 20.
De krommingstensor van Ricci (riccitensor)
is gedefinieerd als de contractie van riemanntensor. Er geldt
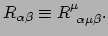 |
(340) |
Bijvoorbeeld in het geval van het aardoppervlak bevat deze tensor
ook de informatie over de kromming, maar dan als de riemanntensor
geïntegreert over de hoeken.
Verder kan men laten zien dat de riccitensor symmetrisch is. Tenslotte hebben
we nog de scalaire kromming, de riccikromming, gedefinieerd door
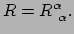 |
(341) |
We hebben nu de tensoren gedefinieerd, die we nodig hebben voor de
beschrijving van fenomenen met de algemene relativiteitstheorie.
Er is een formidabel wiskundig apparaat opgetuigd en we gaan dat
nu eerst gebruiken om de veldvergelijkingen (de zogenaamde einsteinvergelijkingen)
van de ART te poneren. We maken een en ander aannemelijk door een analogie
met de newtoniaanse beschrijving.




Next: Newtoniaanse beschrijving van getijdenkrachten
Up: De algemene relativiteitstheorie
Previous: Geodeten en kromming
Contents
Jo van den Brand
2009-01-31
![]() en
en ![]() .
De vectoren zijn zo klein, dat de kromming van de variëteit geen rol
speelt in het gebied waar dit diagram getekend is. We kunnen daarmee
aannemen dat de vectoren op het oppervlak liggen in plaats van in de
raakruimte. Teneinde de commutator
.
De vectoren zijn zo klein, dat de kromming van de variëteit geen rol
speelt in het gebied waar dit diagram getekend is. We kunnen daarmee
aannemen dat de vectoren op het oppervlak liggen in plaats van in de
raakruimte. Teneinde de commutator
![]() uit te kunnen rekenen,
gebruiken we een lokaal orthonormaal coördinatensysteem. Omdat we
een vector kunnen opvatten als een richtingsafgeleide, stelt
uit te kunnen rekenen,
gebruiken we een lokaal orthonormaal coördinatensysteem. Omdat we
een vector kunnen opvatten als een richtingsafgeleide, stelt
![]() de grootte voor waarmee de
vector
de grootte voor waarmee de
vector ![]() verandert als die langs
verandert als die langs ![]() verplaatst wordt (dat
is de korte gestreepte lijn rechtsboven in Fig 48).
verplaatst wordt (dat
is de korte gestreepte lijn rechtsboven in Fig 48).
![\includegraphics[width=8cm]{Figures/commu.eps}](img1477.png)
![]() en neem er de
dubbele gradiënten van. Dan vinden we
en neem er de
dubbele gradiënten van. Dan vinden we