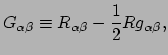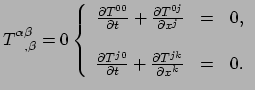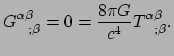Next: Zwakke gravitatievelden en de
Up: De algemene relativiteitstheorie
Previous: Newtoniaanse beschrijving van getijdenkrachten
Contents
We komen nu tot de kern van de ART, de veldvergelijkingen. We zullen proberen
de veldvergelijkingen plausibel te maken op een manier die al het voorgaande
nog eens samenvat. We beginnen met een
beschouwing in Fig. 51 (linker diagram) van de beweging van een deeltje langs
een wereldlijn. De wereldlijn is geparametriseerd met de eigentijd 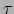 op een klok die het deeltje met zich mee draagt. We kunnen de positie
van het deeltje op een punt van de wereldlijn dus aangeven met
op een klok die het deeltje met zich mee draagt. We kunnen de positie
van het deeltje op een punt van de wereldlijn dus aangeven met
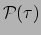 .
.
Figuur 51:
Links: de wereldlijn van een deeltje is een curve die geparametriseerd
kan worden met de eigentijd 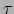 van het deeltje. De snelheid
van het deeltje. De snelheid 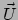 is
de raakvector aan de curve. Rechts: we brengen een coördinatenstelsel
is
de raakvector aan de curve. Rechts: we brengen een coördinatenstelsel
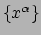 aan. De snelheid
aan. De snelheid 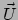 heeft nu componenten
heeft nu componenten
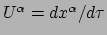 .
.
|
|
De snelheid 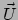 is de raakvector aan de curve en wordt gegeven door
is de raakvector aan de curve en wordt gegeven door
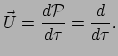 |
(346) |
Voor de snelheid geldt in het LLF op punt

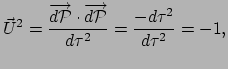 |
(347) |
waarbij we de definitie van de metriek hebben gebruikt70.
Omdat deze vergelijking een getal (scalar) oplevert, is dit geldig in elk
coördinatenstelsel.
We zien dus dat de
snelheid lengte 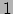 heeft en in de tijdrichting wijst. Merk op dat
deze definities geen gebruik maken van een coördinatenstelsel. In het
geval dat een coördinatenstelsel aangebracht wordt, geldt voor de componenten
van de snelheid
heeft en in de tijdrichting wijst. Merk op dat
deze definities geen gebruik maken van een coördinatenstelsel. In het
geval dat een coördinatenstelsel aangebracht wordt, geldt voor de componenten
van de snelheid
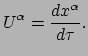 |
(348) |
De componenten zijn dus de afgeleiden van de coördinaten zelf.
Als het deeltje vrij beweegt en er geen andere krachten op werken dan die
ten gevolge van de kromming van ruimtetijd, dan moet het in een rechte
lijn bewegen. Hiermee bedoelen we zo recht als mogelijk is onder invloed van
kromming. Het deeltje dient zijn eigen snelheid parallel
te transporteren. Er geldt
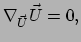 |
(349) |
en dat is, zoals we reeds in vergelijking (333) gezien hebben,
de abstracte uitdrukking voor een geodeet.
Wat dit betekent is dat wanneer je naar een lokaal lorentzframe gaat, de
componenten van de viersnelheid constant blijven (en daarom is
de richtingsafgeleide gelijk aan nul)
als het deeltje slechts een kleine afstand aflegt. We willen nu bekijken
hoe de geodetenvergelijking eruit komt te zien als we een
willekeurig coördinatenstelsel
aanbrengen. Dit is geschetst in het rechterpaneel van Fig. 51.
In dit coördinatenstelsel worden de componenten van 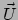 gegeven
door
gegeven
door
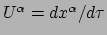 , en kunnen we de geodetenvergelijking
schrijven als
, en kunnen we de geodetenvergelijking
schrijven als
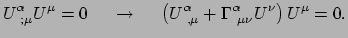 |
(350) |
Merk op dat
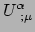 de gradiënt is, waarvan we dan het
inproduct nemen met de snelheid
de gradiënt is, waarvan we dan het
inproduct nemen met de snelheid 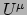 om de afgeleide van de snelheid
in de richting van de snelheid te vinden. Deze afgeleide stellen we
vervolgens gelijk aan nul. In de tweede stap maken we gebruik van de
uitdrukking in componenten van de covariante afgeleide. We vermenigvuldigen
nu de termen en vinden
om de afgeleide van de snelheid
in de richting van de snelheid te vinden. Deze afgeleide stellen we
vervolgens gelijk aan nul. In de tweede stap maken we gebruik van de
uitdrukking in componenten van de covariante afgeleide. We vermenigvuldigen
nu de termen en vinden
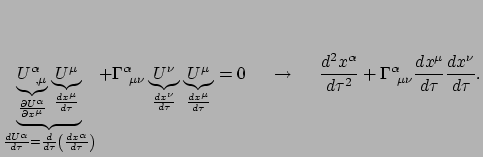 |
(351) |
Het is belangrijk in te zien dat we zijn uitgegaan van de abstracte
tensorvergelijking (355) voor een geodeet. Na het aanbrengen van
een willekeurig coördinatenstelsel hebben we deze vergelijking in
componenten geschreven en het resultaat is vergelijking (357).
Deze laatste geeft vier gewone tweede-orde differentiaalvergelijkingen
voor de coördinaten
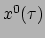 ,
,
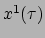 ,
,
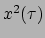 en
en
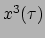 . Deze vergelijkingen zijn gekoppeld via de connectiecoëfficiënten.
Omdat het tweede-orde differentiaalvergelijkingen zijn, hebben we twee
randvoorwaarden nodig, bijvoorbeeld op tijdstip
. Deze vergelijkingen zijn gekoppeld via de connectiecoëfficiënten.
Omdat het tweede-orde differentiaalvergelijkingen zijn, hebben we twee
randvoorwaarden nodig, bijvoorbeeld op tijdstip 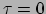 zowel
zowel
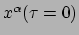 als
als
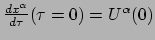 . Daarna ligt
de wereldlijn van het vrije deeltje (geodeet) vast.
. Daarna ligt
de wereldlijn van het vrije deeltje (geodeet) vast.
Figuur:
De wereldlijnen van twee deeltjes zijn initieel parallel.
Door kromming van ruimtetijd bewegen de deeltjes naar elkaar toe.
De afstand tussen de deeltjes wordt gegeven door de ruimtelijke
vector 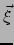 .
.
|
|
We gaan nu weer naar de geodetische afstand tussen twee deeltjes
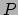 en
en 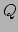 kijken;
zie Fig. 52.
Dit vormt de aanloop tot de einsteinvergelijkingen. Stel dat we twee
deeltjes hebben die op een bepaald tijdstip (dat we voor het gemak
als
kijken;
zie Fig. 52.
Dit vormt de aanloop tot de einsteinvergelijkingen. Stel dat we twee
deeltjes hebben die op een bepaald tijdstip (dat we voor het gemak
als 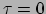 kiezen) in rust zijn ten opzichte van elkaar.
We definiëren de separatievector
kiezen) in rust zijn ten opzichte van elkaar.
We definiëren de separatievector 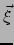 , die van ene naar het andere deeltje wijst.
Verder heeft deeltje
, die van ene naar het andere deeltje wijst.
Verder heeft deeltje 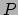 een snelheid
een snelheid 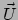 . De eis dat de deeltjes
aanvankelijk in rust zijn ten opzichte van elkaar, komt neer op
. De eis dat de deeltjes
aanvankelijk in rust zijn ten opzichte van elkaar, komt neer op
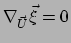 op punt
op punt
 op tijdstip
op tijdstip 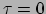 . Verder willen we
. Verder willen we
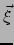 zo definiëren, dat in het LLF van deeltje
zo definiëren, dat in het LLF van deeltje 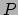 de
vector
de
vector 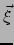 zuiver ruimtelijk is (dat is een keuze die we mogen maken).
Hiermee is
zuiver ruimtelijk is (dat is een keuze die we mogen maken).
Hiermee is 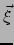 loodrecht op de snelheid
loodrecht op de snelheid 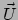 . Hij wijst
dus in een richting die loodrecht op de tijdrichting staat. Er geldt
dan
. Hij wijst
dus in een richting die loodrecht op de tijdrichting staat. Er geldt
dan
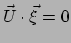 op punt
op punt
 .
Samengevat, eisen we op tijdstip
.
Samengevat, eisen we op tijdstip 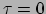
 |
(352) |
De tweede afgeleide
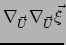 is echter niet gelijk aan nul, want we weten dat de effecten van kromming
merkbaar worden als we tweede-orde afgeleiden van de metriek nemen.
Dit betekent dat de geodeten van de deeltjes naar elkaar
toe worden gedrukt of van elkaar verwijderd raken (algelang de metriek),
naarmate de tijd vordert. Er geldt
is echter niet gelijk aan nul, want we weten dat de effecten van kromming
merkbaar worden als we tweede-orde afgeleiden van de metriek nemen.
Dit betekent dat de geodeten van de deeltjes naar elkaar
toe worden gedrukt of van elkaar verwijderd raken (algelang de metriek),
naarmate de tijd vordert. Er geldt
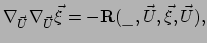 |
(353) |
met 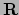 de krommingstensor.
Deze vergelijking beschrijft hoe twee aanvankelijk parallelle geodeten
in de loop der tijd van elkaar beginnen af te wijken ten gevolge van
de kromming. De uitdrukking volgt uit vergelijkingen (330)
en (338). De tweede afgeleide
de krommingstensor.
Deze vergelijking beschrijft hoe twee aanvankelijk parallelle geodeten
in de loop der tijd van elkaar beginnen af te wijken ten gevolge van
de kromming. De uitdrukking volgt uit vergelijkingen (330)
en (338). De tweede afgeleide
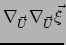 beschrijft de relatieve versnelling van de deeltjes.
beschrijft de relatieve versnelling van de deeltjes.
In het LLF van deeltje 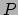 op tijdstip
op tijdstip 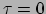 geldt
geldt 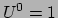 en
en 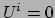 .
Hiermee verwachten we
.
Hiermee verwachten we
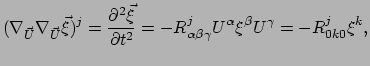 |
(354) |
want de snelheid 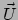 heeft enkel een tijdcomponent in het LLF van deeltje
heeft enkel een tijdcomponent in het LLF van deeltje
 , terwijl de separatievector
, terwijl de separatievector 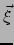 enkel ruimteachtige
componenten heeft
enkel ruimteachtige
componenten heeft 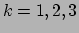 .
In het LLF heeft de vergelijking voor geodetische afwijking de vorm
.
In het LLF heeft de vergelijking voor geodetische afwijking de vorm
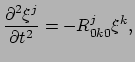 |
(355) |
terwijl we in de newtoniaanse mechanica gevonden hebben (zie vergelijking
(349)) dat
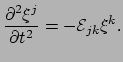 |
(356) |
In een LLF is het ruimtelijke deel van de metriek cartesisch
(
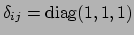 ) en maakt de plaats van de indices niets
uit. Vergelijken geeft dan
) en maakt de plaats van de indices niets
uit. Vergelijken geeft dan
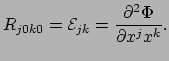 |
(357) |
We kunnen een deel van de krommingstensor identificeren met
afgeleiden van de newtoniaanse
gravitatie potentiaal. Volgens Newton geldt
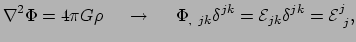 |
(358) |
en we vinden voor het spoor van de gravitationele getijdentensor
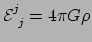 . Analoog zou je misschien verwachten
dat in de algemene relativiteitstheorie zou gelden dat
. Analoog zou je misschien verwachten
dat in de algemene relativiteitstheorie zou gelden dat
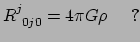 |
(359) |
als een eerste gok.
Er is echter een fundamenteel probleem met vergelijking (365). Het dient een
uitdrukking te zijn, die niet van het coördinatenstelsel afhangt.
Wat we echter gedaan hebben, is het opstellen van de vergelijking in een speciaal
stelsel: het LLF. Wat we derhalve dienen te doen, is proberen een relatie tussen
tensoren te vinden. Hiertoe merken we op dat in het LLF geldt dat
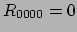 en
en
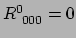 ten gevolge van antisymmetrie.
Er geldt dus
ten gevolge van antisymmetrie.
Er geldt dus
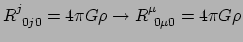 .
We bevinden ons nog steeds in het LLF (overigens geldt hier
.
We bevinden ons nog steeds in het LLF (overigens geldt hier
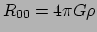 met
met 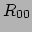 de Ricci tensor, maar dat terzijde).
de Ricci tensor, maar dat terzijde).
Er is nog een probleem met vergelijking (365): links van het
gelijkteken hebben we twee indices en rechts ervan geen enkele. Je zou dus misschien
kunnen denken dat geldt
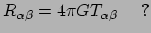 |
(360) |
Hierbij is
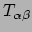 de energie-impuls tensor, waarvan
de energie-impuls tensor, waarvan
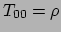 (en dat is overigens
vaak de dominerende term in het LLF). Einstein maakte deze gok al
in 1912, maar hij is fout! Deze vergelijkingen hebben ingebouwde
inconsistenties. Het is belangrijk om te begrijpen wat er mis is, en dat
komt neer op het volgende. Beschouw de riemanntensor
(en dat is overigens
vaak de dominerende term in het LLF). Einstein maakte deze gok al
in 1912, maar hij is fout! Deze vergelijkingen hebben ingebouwde
inconsistenties. Het is belangrijk om te begrijpen wat er mis is, en dat
komt neer op het volgende. Beschouw de riemanntensor
 |
(361) |
Als we de eerste en derde index contraheren, krijgen we
 |
(362) |
We zien hiermee dat de voorgestelde vergelijkingen (366)
een verzameling vormen van 10 partiële differentiaalvergelijkingen voor de 10
componenten van de metriek
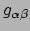 (merk op dat de metriek symmetrisch
is in
(merk op dat de metriek symmetrisch
is in 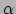 en
en 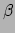 ). Ook de Ricci tensor is symmetrisch. Dat lijkt
allemaal prima, maar we hebben de vrijheid om zelf het coördinatenstelsel
te kiezen waarin we de vergelijkingen gaan opschrijven. We hebben de
vrijheid om
). Ook de Ricci tensor is symmetrisch. Dat lijkt
allemaal prima, maar we hebben de vrijheid om zelf het coördinatenstelsel
te kiezen waarin we de vergelijkingen gaan opschrijven. We hebben de
vrijheid om
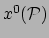 ,
,
,
,
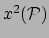 en
en
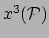 te kiezen. We kunnen dat gebruiken om 4 van de 10
componenten van
te kiezen. We kunnen dat gebruiken om 4 van de 10
componenten van
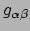 , zoals gezien als functie van de
coördinaten, gelijk te zetten aan wat we willen, bijvoorbeeld
, zoals gezien als functie van de
coördinaten, gelijk te zetten aan wat we willen, bijvoorbeeld
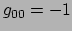 ,
,
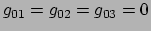 . Echter, onze vergelijkingen
(366) staan dit niet toe: 10 partiële differentiaalvergelijkingen
voor 10 onbekenden. Wat we nodig hebben, zijn 6 vergelijkingen voor 10
onbekenden.
. Echter, onze vergelijkingen
(366) staan dit niet toe: 10 partiële differentiaalvergelijkingen
voor 10 onbekenden. Wat we nodig hebben, zijn 6 vergelijkingen voor 10
onbekenden.
Voordat we onze speurtocht naar de einsteinvergelijkingen voortzetten, maken
we eerst twee opmerkingen. De eerste opmerking heeft te maken met de
Biancchi indentiteiten.
Dankzij deze indentiteiten
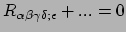 blijkt dat als we de einsteintensor definiëren,
blijkt dat als we de einsteintensor definiëren,
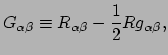 |
(363) |
met
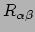 de riccitensor en
de riccitensor en 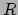 de scalaire kromming, dan
zorgen de Biancchi indentiteiten ervoor dat de divergentie van de einsteintensor
gelijk is aan nul,
de scalaire kromming, dan
zorgen de Biancchi indentiteiten ervoor dat de divergentie van de einsteintensor
gelijk is aan nul,
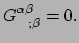 |
(364) |
De tweede opmerking heeft te maken met de ons bekende behoudswetten voor
energie en impuls. In een LLF geldt
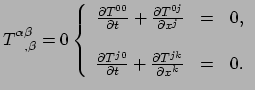 |
(365) |
Merk op dat
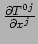 de ruimtelijke divergentie is
en energiebehoud zegt
de ruimtelijke divergentie is
en energiebehoud zegt
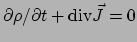 , met
, met
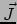 de massa-energieflux. Evenzo is
de massa-energieflux. Evenzo is
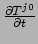 de impulsdichtheid en
de impulsdichtheid en
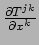 de impulsflux.
Omdat we enkel de eerste afgeleide nemen, is wat geldt in een vlakke ruimte in
het LLF, ook geldig voor gekromde ruimtetijd. Hiermee vinden we de tensorvergelijking
de impulsflux.
Omdat we enkel de eerste afgeleide nemen, is wat geldt in een vlakke ruimte in
het LLF, ook geldig voor gekromde ruimtetijd. Hiermee vinden we de tensorvergelijking
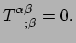 |
(366) |
Het lijkt redelijk om aan te nemen dat de natuur gekozen heeft voor
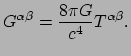 |
(367) |
Dit zijn de einsteinvergelijkingen.
De evenredigheidsfactor (
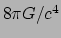 ) vinden we door de newtoniaanse limiet te nemen.
Voordat je de einsteinvergelijkingen oplegt, weet je al dat
) vinden we door de newtoniaanse limiet te nemen.
Voordat je de einsteinvergelijkingen oplegt, weet je al dat
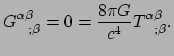 |
(368) |
Dit zijn 4 vergelijkingen en het zijn de afgeleiden van de einsteinvergelijkingen.
Aan deze 4 identiteiten (de divergentie van
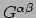 en
en
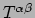 zijn nul) wordt al voldaan. Dit legt 4 beperkingen op aan de einsteinvergelijkingen
(ook wel de veldvergelijkingen genoemd) en de veldvergelijkingen geven slechts
6 nieuwe stukken informatie. Dat is precies wat we nodig hebben.
zijn nul) wordt al voldaan. Dit legt 4 beperkingen op aan de einsteinvergelijkingen
(ook wel de veldvergelijkingen genoemd) en de veldvergelijkingen geven slechts
6 nieuwe stukken informatie. Dat is precies wat we nodig hebben.




Next: Zwakke gravitatievelden en de
Up: De algemene relativiteitstheorie
Previous: Newtoniaanse beschrijving van getijdenkrachten
Contents
Jo van den Brand
2009-01-31
![]() op een klok die het deeltje met zich mee draagt. We kunnen de positie
van het deeltje op een punt van de wereldlijn dus aangeven met
op een klok die het deeltje met zich mee draagt. We kunnen de positie
van het deeltje op een punt van de wereldlijn dus aangeven met
![]() .
.
![\includegraphics[width=12cm]{Figures/curve3.eps}](img1509.png)
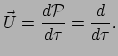
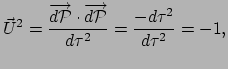
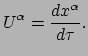
![\includegraphics[width=6cm]{Figures/geod3.eps}](img1528.png)
![]() en
en ![]() kijken;
zie Fig. 52.
Dit vormt de aanloop tot de einsteinvergelijkingen. Stel dat we twee
deeltjes hebben die op een bepaald tijdstip (dat we voor het gemak
als
kijken;
zie Fig. 52.
Dit vormt de aanloop tot de einsteinvergelijkingen. Stel dat we twee
deeltjes hebben die op een bepaald tijdstip (dat we voor het gemak
als ![]() kiezen) in rust zijn ten opzichte van elkaar.
We definiëren de separatievector
kiezen) in rust zijn ten opzichte van elkaar.
We definiëren de separatievector ![]() , die van ene naar het andere deeltje wijst.
Verder heeft deeltje
, die van ene naar het andere deeltje wijst.
Verder heeft deeltje ![]() een snelheid
een snelheid ![]() . De eis dat de deeltjes
aanvankelijk in rust zijn ten opzichte van elkaar, komt neer op
. De eis dat de deeltjes
aanvankelijk in rust zijn ten opzichte van elkaar, komt neer op
![]() op punt
op punt
![]() op tijdstip
op tijdstip ![]() . Verder willen we
. Verder willen we
![]() zo definiëren, dat in het LLF van deeltje
zo definiëren, dat in het LLF van deeltje ![]() de
vector
de
vector ![]() zuiver ruimtelijk is (dat is een keuze die we mogen maken).
Hiermee is
zuiver ruimtelijk is (dat is een keuze die we mogen maken).
Hiermee is ![]() loodrecht op de snelheid
loodrecht op de snelheid ![]() . Hij wijst
dus in een richting die loodrecht op de tijdrichting staat. Er geldt
dan
. Hij wijst
dus in een richting die loodrecht op de tijdrichting staat. Er geldt
dan
![]() op punt
op punt
![]() .
Samengevat, eisen we op tijdstip
.
Samengevat, eisen we op tijdstip ![]()

![]() op tijdstip
op tijdstip ![]() geldt
geldt ![]() en
en ![]() .
Hiermee verwachten we
.
Hiermee verwachten we
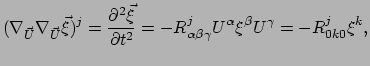
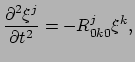
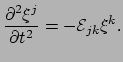
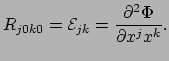
![]() en
en
![]() ten gevolge van antisymmetrie.
Er geldt dus
ten gevolge van antisymmetrie.
Er geldt dus
![]() .
We bevinden ons nog steeds in het LLF (overigens geldt hier
.
We bevinden ons nog steeds in het LLF (overigens geldt hier
![]() met
met ![]() de Ricci tensor, maar dat terzijde).
de Ricci tensor, maar dat terzijde).
![]() blijkt dat als we de einsteintensor definiëren,
blijkt dat als we de einsteintensor definiëren,