



Next: De zwakke-veld limiet van
Up: De algemene relativiteitstheorie
Previous: De einsteinvergelijkingen
Contents
Het is duidelijk dat de ART beschrijving van gravitatie in termen van kromming van
ruimtetijd reduceert tot de SRT voor lokale lorentzframes. Het is echter belangrijk
om expliciet te controleren dat de beschrijving reduceert tot de newtoniaanse
beschrijving als we de correcte randvoorwaarden bezien.
Zonder gravitatie heeft ruimtetijd de minkowskimetriek. Derhalve zullen zwakke
gravitatievelden overeenkomen met een geringe kromming van ruimtetijd. We nemen
aan dat er coördinaten bestaan, waarin de metriek de volgende vorm heeft,
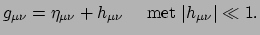 |
(369) |
Verder nemen we aan dat in dat coördinatenstelsel de metriek stationair is,
waardoor geldt
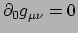 . De wereldlijn van een vrijvallend
deeltje wordt gegeven door de geodetische vergelijking
. De wereldlijn van een vrijvallend
deeltje wordt gegeven door de geodetische vergelijking
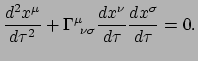 |
(370) |
We nemen aan dat het deeltje langzaam beweegt (niet-relativistisch), zodat
voor de componenten van de driesnelheid geldt
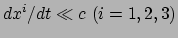 ,
met
,
met 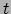 gedefinieerd via
gedefinieerd via 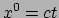 . Hiermee eisen we voor
. Hiermee eisen we voor 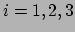
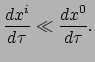 |
(371) |
We mogen de driesnelheid verwaarlozen en vinden
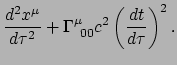 |
(372) |
We gebruiken vergelijking (303) en vinden
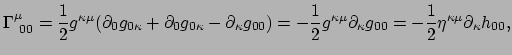 |
(373) |
waarbij we vergelijking (375) hebben gebruikt. De laatste
gelijkheid is geldig tot op eerste orde in
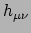 .
Omdat we hebben aangenomen dat de metriek stationair is geldt
.
Omdat we hebben aangenomen dat de metriek stationair is geldt
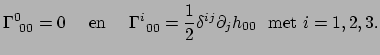 |
(374) |
Invullen in vergelijking (378) levert
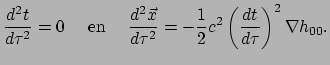 |
(375) |
De eerste vergelijking stelt dat
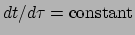 ,
en hiermee kunnen we de twee uitdrukkingen combineren. Dat geeft
de volgende bewegingsvergelijking voor het deeltje,
,
en hiermee kunnen we de twee uitdrukkingen combineren. Dat geeft
de volgende bewegingsvergelijking voor het deeltje,
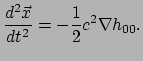 |
(376) |
Als we deze uitdrukking vergelijken met de newtoniaanse uitdrukking
voor de beweging van een deeltje in een gravitatieveld, formule
(15), dan zien we dat beide identiek zijn, als we de
identificatie maken dat
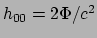 .
We vinden dat voor een langzaam bewegend deeltje de ART overgaat
in de newtoniaanse beschrijving, als we de metriek gegeven wordt door
.
We vinden dat voor een langzaam bewegend deeltje de ART overgaat
in de newtoniaanse beschrijving, als we de metriek gegeven wordt door
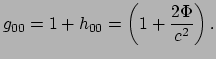 |
(377) |
We kunnen een schatting maken van deze correctie op de
minkowskimetriek, want
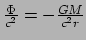 en we vinden
en we vinden 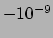 aan het aardoppervlak,
aan het aardoppervlak, 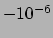 aan
het oppervlak van de zon, en
aan
het oppervlak van de zon, en 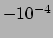 aan het oppervlak van een
witte dwerg. We zien dat de zwakke-veld limiet een uitstekende
benadering is.
aan het oppervlak van een
witte dwerg. We zien dat de zwakke-veld limiet een uitstekende
benadering is.
Vergelijking (383) toont dat ruimtetijdkromming ervoor
zorgt dat de tijdcoördinaat 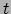 in het algemeen niet de eigentijd
meet. Hiertoe nemen we een klok die in rust is op een bepaald punt
in ons coördinatensysteem (dan geldt
in het algemeen niet de eigentijd
meet. Hiertoe nemen we een klok die in rust is op een bepaald punt
in ons coördinatensysteem (dan geldt
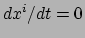 ). Het
eigentijd interval
). Het
eigentijd interval 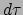 tussen twee tikken van deze klok wordt
gegeven door
tussen twee tikken van deze klok wordt
gegeven door
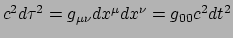 ,
waarmee we vinden
,
waarmee we vinden
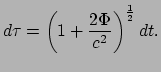 |
(378) |
Dit geeft het interval in eigentijd 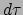 dat correspondeert met
een interval
dat correspondeert met
een interval 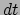 in coördinatentijd voor een stationaire waarnemer
in de buurt van een massief object, in een gebied met gravitatie
potentiaal
in coördinatentijd voor een stationaire waarnemer
in de buurt van een massief object, in een gebied met gravitatie
potentiaal 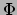 , Omdat
, Omdat 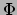 negatief is, is dit eigentijd interval
korter dan het corresponderende interval voor een stationaire waarnemer
op grote afstand van het object, waar
negatief is, is dit eigentijd interval
korter dan het corresponderende interval voor een stationaire waarnemer
op grote afstand van het object, waar
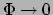 en
dus
en
dus
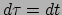 . Merk op dat we dit reeds hebben afgeleid uit het
equivalentieprincipe; zie vergelijking (9) met
. Merk op dat we dit reeds hebben afgeleid uit het
equivalentieprincipe; zie vergelijking (9) met 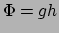 .
.
Figuur 53:
Banen van een bal en een kogel door de ruimte. Gezien vanuit een
laboratorium hebben de banen een verschillende kromming.
|
|
Het ruimtetijdinterval wordt gegeven door
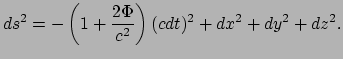 |
(379) |
Deze vergelijking beschrijft een geometrie van ruimtetijd waarin deeltjes
op geodeten bewegen die precies dezelfde banen volgen als die van
deeltjes in een vlakke ruimtetijd waarin de newtoniaanse gravitatiekracht
actief is. We hebben hiermee in gekromde ruimtetijd beeld gevonden
voor Newton's gravitatie. De kromming is enkel in de tijdrichting.
Kromming in de tijd is niets anders dan de gravitationele roodverschuiving:
tijd schrijdt voort met verschillende snelheid op verschillende plaatsen,
derhalve is tijd gekromd. Deze gravitationele roodverschuiving bepaalt
volledig de banen van deeltjes in een gravitatieveld. De gehele
newtoniaanse gravitatie is enkel tijdkromming.
Wellicht gaat het bovenstaande tegen ons gevoel in. Immers niets lijkt zo
vanzelfsprekend als het idee dat gravitatie een manifestatie is van
kromming van de ruimte.
Kijk bijvoorbeeld naar de banen van twee
objecten in de ruimte, zoals getoond in Fig. 53.
Een van de objecten is een bal die met een relatief lage snelheid
van 5 m/s beweegt en een hoogte bereikt van 5 m. Het andere
object is de kogel uit een geweer. Deze kogel beweegt met hoge
snelheid (500 m/s). Als we de figuur bekijken, dan lijkt de
baan van de bal sterker gekromd dan die van de kogel.
Het punt is echter dat we niet naar een kromming van de ruimte dienen
te kijken, maar naar de kromming van ruimtetijd. Hiertoe tekenen we
de banen nogmaals in Fig. 54, maar nu in
minkowski ruimtetijd. We zien dat nu de banen van de ballen een
gelijke kromming hebben in ruimtetijd.
Figuur 54:
Banen van een bal en een kogel door ruimtetijd. Gezien vanuit een
laboratorium hebben de banen dezelfde kromming. We vergelijken de
baanlengte ten opzichte van de booglengte van de cirkel: (straal)
= (horizontale afstand)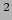 / 8(hoogte).
/ 8(hoogte).
|
|
In werkelijkheid heeft echter geen van de banen een kromming! Ze zien
er gekromd uit omdat we vergeten zijn dat de ruimtetijd waarin ze
getekend zijn, zelf gekromd is. De kromming van ruimtetijd is precies
zodanig, dat de banen zelf volledig recht zijn: het zijn immers geodeten.




Next: De zwakke-veld limiet van
Up: De algemene relativiteitstheorie
Previous: De einsteinvergelijkingen
Contents
Jo van den Brand
2009-01-31
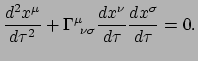
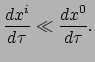
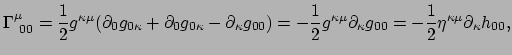
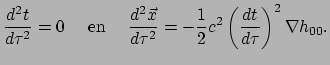
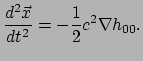
![]() in het algemeen niet de eigentijd
meet. Hiertoe nemen we een klok die in rust is op een bepaald punt
in ons coördinatensysteem (dan geldt
in het algemeen niet de eigentijd
meet. Hiertoe nemen we een klok die in rust is op een bepaald punt
in ons coördinatensysteem (dan geldt
![]() ). Het
eigentijd interval
). Het
eigentijd interval ![]() tussen twee tikken van deze klok wordt
gegeven door
tussen twee tikken van deze klok wordt
gegeven door
![]() ,
waarmee we vinden
,
waarmee we vinden
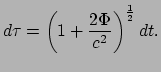
![\includegraphics[width=10cm]{Figures/ballen.eps}](img1600.png)
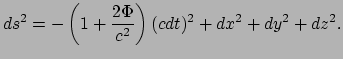
![\includegraphics[width=12cm]{Figures/ballenrt.eps}](img1602.png)