We zijn nu op het punt aangekomen dat we ons kunnen buigen over de vraag hoe snelheden
veranderen tussen waarnemers die zich bewegen ten opzichte van elkaar. Snelheid is
niets anders dan een verandering van positie gedeeld door de verstreken tijd
benodigd om de afstand tussen de begin en eindposities te overbruggen. Maar zoals al gezien,
zijn afgelegde afstanden en verstreken tijden niet meer absoluut: zij verschillen
van waarnemer tot waarnemer. Het is dan ook te verwachten dat het concept gemeten
snelheid op een nieuwe manier zal transformeren tussen verschillende waarnemers.
Hiervoor beschouwen we twee waarnemers, 1 en 2, die
ten opzichte van elkaar bewegen met een constante snelheid ![]() . Beiden kijken
naar een bewegend deeltje, en meten daar de snelheid van, waarbij
. Beiden kijken
naar een bewegend deeltje, en meten daar de snelheid van, waarbij ![]() de snelheid
is zoals gemeten door waarnemer 1, en
de snelheid
is zoals gemeten door waarnemer 1, en ![]() de snelheid zoals gemeten door
waarnemer 2. De vraag is nu hoe deze twee gemeten snelheden zich tot elkaar
verhouden.
de snelheid zoals gemeten door
waarnemer 2. De vraag is nu hoe deze twee gemeten snelheden zich tot elkaar
verhouden.
Per definitie is de snelheid zoals gemeten door waarnemer 2 gegeven door
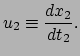 |
(189) |
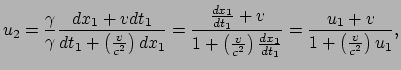 |
(190) |
Dit is de zogenaamde regel van Einstein voor het samenstellen van snelheden:
gegeven de snelheid ![]() van een
object zoals gemeten door waarnemer 1, geeft deze formule ons de snelheid
van een
object zoals gemeten door waarnemer 1, geeft deze formule ons de snelheid ![]() van
dit object zoals gemeten door waarnemer 2 die zich zelf met snelheid
van
dit object zoals gemeten door waarnemer 2 die zich zelf met snelheid ![]() beweegt ten
opzichte van waarnemer 1. Voor kleine snelheden gaat de relatie over in de normale
optelling van snelheden in de klassieke mechanica:
beweegt ten
opzichte van waarnemer 1. Voor kleine snelheden gaat de relatie over in de normale
optelling van snelheden in de klassieke mechanica:
![]() .
.
Een aantal interessantie eigenschappen kan nu worden opgemerkt. Zo kan eenvoudig
worden aangetoond dat als een waarnemer een deeltje ziet bewegen met een snelheid
lager dan de lichtsnelheid (oftewel ![]() ), elke andere waarnemer dit deeltje
ook ziet bewegen met een snelheid lager dan de lichtsnelheid (
), elke andere waarnemer dit deeltje
ook ziet bewegen met een snelheid lager dan de lichtsnelheid (![]() ). Ook kan
worden aangetoond dat als een waarnemer het deeltje ziet bewegen met een snelheid
hoger dan de lichtsnelheid, elke andere waarnemer dit deeltje ook ziet bewegen met
een snelheid hoger dan de lichtsnelheid. Dit laatste is overigens alleen wiskundig
waar: het zal later worden aangetoond dat niets sneller kan gaan dan het
licht53.
). Ook kan
worden aangetoond dat als een waarnemer het deeltje ziet bewegen met een snelheid
hoger dan de lichtsnelheid, elke andere waarnemer dit deeltje ook ziet bewegen met
een snelheid hoger dan de lichtsnelheid. Dit laatste is overigens alleen wiskundig
waar: het zal later worden aangetoond dat niets sneller kan gaan dan het
licht53.
Ht belangrijkste gevolg van Einstein's snelheidsregel is dat alle
waarnemers dezelfde snelheid voor een lichtsignaal zullen meten, ongeacht de onderlinge
snelheden tussen deze waarnemers: voor elke waarnemer zal een foton zich voortplanten
met snelheid ![]() . Neem als bewegend object een foton, dat voor waarnemer 1 met een
snelheid van
. Neem als bewegend object een foton, dat voor waarnemer 1 met een
snelheid van ![]() beweegt. Einstein's snelheidsregel zegt dan vervolgens dat
ook waarnemer 2 dit foton met snelheid
beweegt. Einstein's snelheidsregel zegt dan vervolgens dat
ook waarnemer 2 dit foton met snelheid ![]() ziet bewegen,
ziet bewegen,
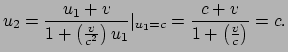 |
(191) |
Tijddilatatie kan ook direct worden afgeleid uit de constantheid van de
lichtsnelheid voor verschillende waarnemers. Om dit duidelijk te maken
beschouwen we een eenvoudige klok gebaseerd op reflecterend licht. De
klok is weergegeven in Fig. 38.
![\includegraphics[width=14cm]{Figures/time.eps}](img1003.png)
|
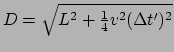 . Invullen en
oplossen van
. Invullen en
oplossen van
Een goed voorbeeld van tijddilatatie zijn muonen die gecreëerd worden
in de buitenste laag van de aardatmosfeer en richting de aarde bewegen.
Vanwege tijddilatatie is hun levensduur beduidend langer dan de
levensduur zoals die op aarde (in het rustsysteem van de muonen) gemeten
wordt: 2.2 ![]() s. Dit laat toe dat dergelijke kosmische muonen een
grotere weg afleggen en het oppervlak van de aarde bereiken kunnen.
Voor een waarnemer die meereist met een muon nadert de aarde met een
snelheid in de buurt van de lichtsnelheid, maar kan de afgelegde weg desondanks
niet meer dan
s. Dit laat toe dat dergelijke kosmische muonen een
grotere weg afleggen en het oppervlak van de aarde bereiken kunnen.
Voor een waarnemer die meereist met een muon nadert de aarde met een
snelheid in de buurt van de lichtsnelheid, maar kan de afgelegde weg desondanks
niet meer dan
![]() m afleggen. Toch bereiken deze muonen het aardoppervlak, terwijl
de afstand van de buitenste laag van de atmosfeer tot het oppervlak
ongeveer 20 km is. De verklaring is dat deze lengte van 20 km voor
de meereizende waarnemer lorentz-gecontraheerd is tot minder dan 660 m.
m afleggen. Toch bereiken deze muonen het aardoppervlak, terwijl
de afstand van de buitenste laag van de atmosfeer tot het oppervlak
ongeveer 20 km is. De verklaring is dat deze lengte van 20 km voor
de meereizende waarnemer lorentz-gecontraheerd is tot minder dan 660 m.
We kunnen onze lichtklok ook gebruiken om lorentzcontractie te begrijpen.
We tonen de geometrie in Fig. 39.
![\includegraphics[width=14cm]{Figures/contr.eps}](img1011.png)
|
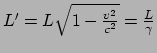 .
.