



Next: Invariantie van de lichtsnelheid
Up: De speciale relativiteitstheorie
Previous: Lorentzcontractie
Contents
Uit het relativiteitsprincipe volgde al dat het lijnelement invariant dient te zijn
onder transformaties van coördinaten. Dit betekent dat er een beperkte set waarnemers is
die onderling het minkowksilijnelement mogen gebruiken. We vragen ons af
welke transformaties tussen waarnemers het minkowskilijnelement niet van vorm doen
veranderen.
Wiskundig gezien is dan ook de vraag welke functies
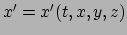 ,
,
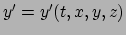 ,
,
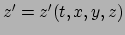 de volgende vergelijking
oplossen,
de volgende vergelijking
oplossen,
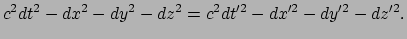 |
(172) |
Er zijn meerdere transformaties te bedenken die hieraan voldoen. De makkelijkste die
we bedenken kunnen is dat we gewoon bij elke coordinaat een constante optellen,
 |
(173) |
Ingevuld in vergelijking (178)
laat direct zien dat dit een oplossing is. Fysisch betekent deze
oplossing niets anders dan dat de twee waarnemers een (vaste) afstand van elkaar
staan (
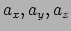 ), en dat de klok van een van de waarnemers een (vaste) hoeveelheid
tijd voor of achter
loopt op die van de ander (
), en dat de klok van een van de waarnemers een (vaste) hoeveelheid
tijd voor of achter
loopt op die van de ander (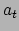 ). Zulke transformaties noemt men translaties.
). Zulke transformaties noemt men translaties.
Een tweede set transformaties die het lijnelement gegeven in vergelijking (178)
invariant laten, kan gevonden worden door veranderingen
in de tijd en één van de plaats-coördinaten (bijvoorbeeld 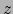 ) niet te beschouwen. In dat
geval moet voldaan worden aan
) niet te beschouwen. In dat
geval moet voldaan worden aan
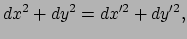 |
(174) |
oftewel de som van twee kwadraten dient niet te veranderen. Deze vergelijking is
eenvoudig op te lossen door te schrijven
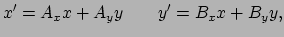 |
(175) |
waar
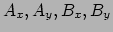 constanten zijn. Ingevuld in vergelijking (180)
laat dan zien dat voor deze constanten dient te gelden
constanten zijn. Ingevuld in vergelijking (180)
laat dan zien dat voor deze constanten dient te gelden
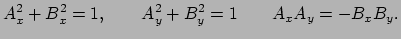 |
(176) |
Aan de eerste twee eisen kan direct voldaan worden: als een som van twee kwadraten
een constante moet opleveren, dan ligt het voor de hand om sinussen en cosinussen te
proberen, aangezien voor deze functies geldt
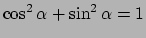 voor
elke hoek
voor
elke hoek 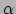 . Men kan dus kiezen
. Men kan dus kiezen
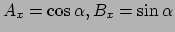 en
en
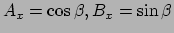 om aan de eerste twee vergelijkingen te voldoen;
aan de derde vergelijking is dan ook voldaan wanneer gekozen wordt
om aan de eerste twee vergelijkingen te voldoen;
aan de derde vergelijking is dan ook voldaan wanneer gekozen wordt
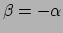 .
Op deze manier is de transformatie compleet, en vinden we
.
Op deze manier is de transformatie compleet, en vinden we
Deze transformatie correspondeert met een
draaiing om de 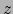 -as over een hoek
-as over een hoek 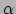 . Bijvoorbeeld, als die hoek
. Bijvoorbeeld, als die hoek
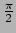 is
(een draaiing van
is
(een draaiing van 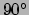 ), dan is
), dan is 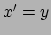 , en
, en 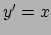 : de twee waarnemers staan
stil ten opzichte van elkaar, maar zijn onderling
: de twee waarnemers staan
stil ten opzichte van elkaar, maar zijn onderling 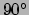 gedraaid. Transformaties
als deze heten rotaties. In het voorgaande hebben we alleen een draaiing over
de
gedraaid. Transformaties
als deze heten rotaties. In het voorgaande hebben we alleen een draaiing over
de 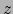 -as beschouwd, maar de uitbreiding naar draaiingen over de andere assen zijn
net zo eenvoudig te vinden.
-as beschouwd, maar de uitbreiding naar draaiingen over de andere assen zijn
net zo eenvoudig te vinden.
Een derde soort transformatie kan gevonden worden door nu niet de tijd en een
plaatscoördinaat constant te houden, maar in plaats daarvan twee ruimtelijke coördinaten
(bijvoorbeeld 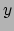 en
en 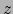 ). In dat geval dient de transformatie te voldoen aan
). In dat geval dient de transformatie te voldoen aan
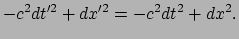 |
(178) |
Door nu te schrijven
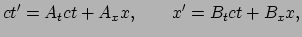 |
(179) |
(waar 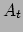 ,
, 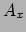 ,
, 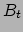 ,
, 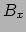 constanten zijn) en in te vullen in vergelijking (184),
wordt gevonden dat de constanten moeten voldoen aan
constanten zijn) en in te vullen in vergelijking (184),
wordt gevonden dat de constanten moeten voldoen aan
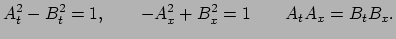 |
(180) |
Deze keer zullen sinussen en cosinussen niet voldoen, omdat hier nu het
verschil van twee kwadraten een constante moet zijn om aan de eerste
twee vergelijkingen te voldoen. Dit is precies wat de hyperbolische functies
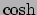 en
en 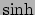 definieert: voor deze geldt namelijk dat
definieert: voor deze geldt namelijk dat
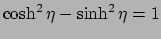 ,
voor elke waarde van
,
voor elke waarde van 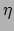 . Het ligt dan ook voor de hand te kiezen
. Het ligt dan ook voor de hand te kiezen
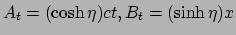 en
en
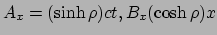 zodat aan de eerste twee vergelijkingen is voldaan. Aan de derde vergelijking kan
vervolgens voldaan worden door
zodat aan de eerste twee vergelijkingen is voldaan. Aan de derde vergelijking kan
vervolgens voldaan worden door
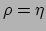 te kiezen. Hiermee is dan de transformatie
compleet, en vinden we
te kiezen. Hiermee is dan de transformatie
compleet, en vinden we
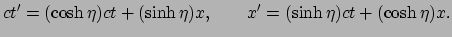 |
(181) |
Wiskundig is dit een draaiing in ruimtetijd, maar dan over een
`hyperbolische hoek' 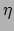 in plaats van een normale. Maar wat betekent dit
fysisch? Met name: wat is de betekenis van de hyperbolische hoek
in plaats van een normale. Maar wat betekent dit
fysisch? Met name: wat is de betekenis van de hyperbolische hoek 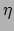 ? Dit kan
worden gevonden door de tijddilatatie te beschouwen: we hadden al gezien dat de tijden
van twee waarnemers die met snelheid
? Dit kan
worden gevonden door de tijddilatatie te beschouwen: we hadden al gezien dat de tijden
van twee waarnemers die met snelheid 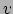 ten opzichte van elkaar bewegen, gerelateerd
zijn via vergelijking (172).
Als we de differentiaalvorm nemen van vergelijking (187)
en kiezen
ten opzichte van elkaar bewegen, gerelateerd
zijn via vergelijking (172).
Als we de differentiaalvorm nemen van vergelijking (187)
en kiezen 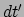 =
= 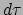 , dan
kunnen we de eerste uitdrukking in vergelijking (187) schrijven als
, dan
kunnen we de eerste uitdrukking in vergelijking (187) schrijven als
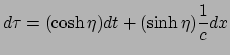 |
(182) |
Kwadrateren, delen door 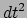 en vergelijken met de tijddilatatie formule
geeft dan
en vergelijken met de tijddilatatie formule
geeft dan
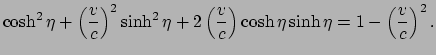 |
(183) |
Dit is een kwadratische vergelijking voor de variabele
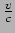 , en geeft een
relatie tussen de snelheid
, en geeft een
relatie tussen de snelheid 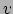 en de hyperbolische hoek
en de hyperbolische hoek 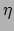 . Zo is al meteen te zien
dat
. Zo is al meteen te zien
dat 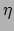 niets anders is dan een ingewikkelde manier om de snelheid tussen twee
waarnemers te beschrijven51.
Wat de precieze relatie is tussen
niets anders is dan een ingewikkelde manier om de snelheid tussen twee
waarnemers te beschrijven51.
Wat de precieze relatie is tussen 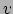 en
en 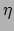 vraagt nog een beetje meer rekenwerk.
Allereerst moet vergelijking (189) herschreven worden tot
vraagt nog een beetje meer rekenwerk.
Allereerst moet vergelijking (189) herschreven worden tot
waar in de laatste stap de relatie
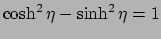 is gebruikt.
Deze vergelijking kan worden opgelost voor
is gebruikt.
Deze vergelijking kan worden opgelost voor
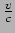 met behulp van de abc-formule.
Het resultaat is het directe verband tussen
met behulp van de abc-formule.
Het resultaat is het directe verband tussen
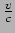 en
en 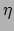 ,
,
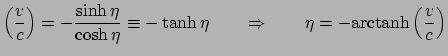 |
(185) |
Dit kan nu worden gebruikt om de transformatievergelijking (191)
uit te drukken in de snelheid 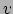 ,
wat vaak een inzichtelijker grootheid is dan de hyperbolische hoek
,
wat vaak een inzichtelijker grootheid is dan de hyperbolische hoek 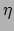 . Hiervoor
kunnen de volgende rekenregels worden gebruikt52,
. Hiervoor
kunnen de volgende rekenregels worden gebruikt52,
Merk op dat de lorentzfactor 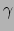 hier op natuurlijke wijze zijn intrede doet.
Hiermee is dan gevonden dat de transformaties tussen de twee waarnemers gegeven worden door
hier op natuurlijke wijze zijn intrede doet.
Hiermee is dan gevonden dat de transformaties tussen de twee waarnemers gegeven worden door
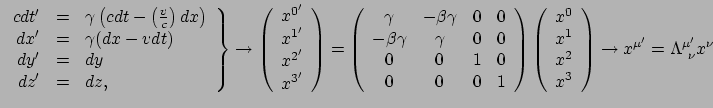 |
(187) |
(waar de relaties tussen de 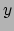 en
en 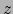 afstanden ook weer zijn toegevoegd).
Hierbij is
afstanden ook weer zijn toegevoegd).
Hierbij is
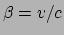 de snelheid als fractie van de lichtsnelheid.
Verder gebruiken we
de snelheid als fractie van de lichtsnelheid.
Verder gebruiken we 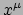 met
met 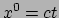 ,
, 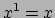 ,
, 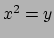 en
en 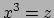 , alsook
de transformatiematrix
, alsook
de transformatiematrix
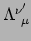 .
.
De inverse transformaties kunnen we vinden door 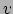 door
door 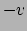 te vervangen. We vinden
te vervangen. We vinden
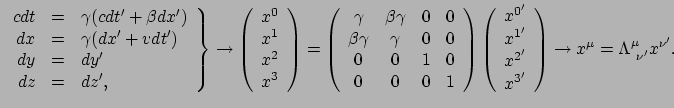 |
(188) |
We zien dan dat vergelijking (193) geschreven
kan worden als
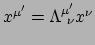 , terwijl
voor de inverse relaties (194) geldt
, terwijl
voor de inverse relaties (194) geldt
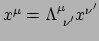 .
Deze vergelijkingen heten de lorentztransformaties, en spelen een hoofdrol in
de SRT. Fysisch stellen zij het verschil voor tussen
afstanden en tijdsduren zoals gemeten door waarnemers die zich ten opzichte
van elkaar bewegen met een constante snelheid
.
Deze vergelijkingen heten de lorentztransformaties, en spelen een hoofdrol in
de SRT. Fysisch stellen zij het verschil voor tussen
afstanden en tijdsduren zoals gemeten door waarnemers die zich ten opzichte
van elkaar bewegen met een constante snelheid 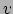 in
in 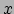 -richting. Zulke vergelijkingen
zijn eenvoudig af te leiden voor waarnemers die zich met snelheid
-richting. Zulke vergelijkingen
zijn eenvoudig af te leiden voor waarnemers die zich met snelheid 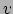 in andere
richtingen bewegen. Tezamen met de translaties in alle richtingen en de rotaties om
de drie ruimte-assen, vormen de lorentztransformaties de volledige set transformaties
die het lijnelement niet veranderen, oftewel: onder deze transformaties is het
relativiteitprincipe veilig gesteld. De conclusie is dan ook de volgende: zolang
waarnemers maar louter getransleerd en/of geroteerd zijn ten opzichte van elkaar, of
alleen met constante snelheid ten opzichte van elkaar bewegen, kunnen zij allen het
minkowskilijnelement blijven gebruiken, en gelden dus alle wetten afgeleid in dit
hoofstuk voor de coördinaatsystemen voor al zulke waarnemers. Zulke stelsels noemen
we inertiaalstelsels. Dit is wat de speciale relativititeitstheorie het
predikaat `speciaal' geeft: alle wetten afgeleid gelden voor een beperkte set
waarnemers. In latere hoofdstukken zullen we onze bevindingen uitbreiden naar
alle waarnemers, leidend tot de theorie van de algemene relativiteit.
Voor nu zullen we in de rest van dit hoofdstuk altijd louter inertiaalstelsels
beschouwen: vanaf nu zal er met `waarnemer' een waarnemer bedoeld worden die zich
in een inertiaalstelsel bevindt.
in andere
richtingen bewegen. Tezamen met de translaties in alle richtingen en de rotaties om
de drie ruimte-assen, vormen de lorentztransformaties de volledige set transformaties
die het lijnelement niet veranderen, oftewel: onder deze transformaties is het
relativiteitprincipe veilig gesteld. De conclusie is dan ook de volgende: zolang
waarnemers maar louter getransleerd en/of geroteerd zijn ten opzichte van elkaar, of
alleen met constante snelheid ten opzichte van elkaar bewegen, kunnen zij allen het
minkowskilijnelement blijven gebruiken, en gelden dus alle wetten afgeleid in dit
hoofstuk voor de coördinaatsystemen voor al zulke waarnemers. Zulke stelsels noemen
we inertiaalstelsels. Dit is wat de speciale relativititeitstheorie het
predikaat `speciaal' geeft: alle wetten afgeleid gelden voor een beperkte set
waarnemers. In latere hoofdstukken zullen we onze bevindingen uitbreiden naar
alle waarnemers, leidend tot de theorie van de algemene relativiteit.
Voor nu zullen we in de rest van dit hoofdstuk altijd louter inertiaalstelsels
beschouwen: vanaf nu zal er met `waarnemer' een waarnemer bedoeld worden die zich
in een inertiaalstelsel bevindt.
De lorentztransformaties geven ons alle mogelijke relaties tussen de tijdsduren
en afstanden zoals gemeten door verschillende waarnemers die zich bewegen met
snelheid 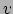 ten opzichte van elkaar. Twee specifieke voorbeelden van zulke relaties
hadden we al eerder gezien, toen nog direct afgeleid uit het minkowskilijnelement:
de tijddilatatie en de lorentzcontractie. Deze liggen dan ook automatisch opgesloten
in de lorentztransformaties. Voor tijddilatatie hoeven we alleen maar te kijken
naar het speciale geval dat een van de waarnemers een tijdsduur meet tussen
twee gebeurtenissen die ten opzichte van hem op een en dezelfde positie plaatsvinden,
zodat
ten opzichte van elkaar. Twee specifieke voorbeelden van zulke relaties
hadden we al eerder gezien, toen nog direct afgeleid uit het minkowskilijnelement:
de tijddilatatie en de lorentzcontractie. Deze liggen dan ook automatisch opgesloten
in de lorentztransformaties. Voor tijddilatatie hoeven we alleen maar te kijken
naar het speciale geval dat een van de waarnemers een tijdsduur meet tussen
twee gebeurtenissen die ten opzichte van hem op een en dezelfde positie plaatsvinden,
zodat 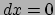 ; voor deze waarnemer schrijven we
; voor deze waarnemer schrijven we
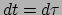 ;
er volgt dan direct uit vergelijking (194)
dat een andere waarnemer een tijdsduur meet tussen
deze twee gebeurtenissen gelijk aan
;
er volgt dan direct uit vergelijking (194)
dat een andere waarnemer een tijdsduur meet tussen
deze twee gebeurtenissen gelijk aan
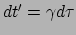 . Dit is precies de
tijddilatatieformule in vergelijking (172).
Verder, om de lorentzcontractie af te leiden uit
de lorentztransformaties hoeft alleen naar het speciale geval gekeken te worden
dat de twee gebeurtenissen de metingen zijn van voor- en achterkant van een lat
door een waarnemer die deze metingen doet op een en hetzelfde tijdstip (immers:
als dat niet het geval is, zal de lat `voorbij' vliegen in de tijd die deze waarnemer
wacht tussen meting van voor- en achterkant, en stelt de afstand tussen gemeten
positie van voor- en achterkant dus niet meer de lengte van de lat voor). Voor
deze waarnemer geldt dan ook
. Dit is precies de
tijddilatatieformule in vergelijking (172).
Verder, om de lorentzcontractie af te leiden uit
de lorentztransformaties hoeft alleen naar het speciale geval gekeken te worden
dat de twee gebeurtenissen de metingen zijn van voor- en achterkant van een lat
door een waarnemer die deze metingen doet op een en hetzelfde tijdstip (immers:
als dat niet het geval is, zal de lat `voorbij' vliegen in de tijd die deze waarnemer
wacht tussen meting van voor- en achterkant, en stelt de afstand tussen gemeten
positie van voor- en achterkant dus niet meer de lengte van de lat voor). Voor
deze waarnemer geldt dan ook 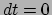 , en zal de lengte van de lat gegeven zijn
door
, en zal de lengte van de lat gegeven zijn
door 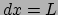 ; volgens vergelijking (194)
meet de waarnemer in rust ten opzichte van de lat een
lengte van
; volgens vergelijking (194)
meet de waarnemer in rust ten opzichte van de lat een
lengte van
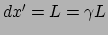 . Dit is
precies de lorentzcontractie formule, vergelijking (177).
. Dit is
precies de lorentzcontractie formule, vergelijking (177).
De tijddilatatie en lorentzcontractie zijn slechts
speciale gevallen van de lorentztransformaties, een set algemene
relaties tussen tijdsduren en afstanden zoals gemeten door waarnemers die bewegen
ten opzichte van elkaar met een snelheid 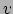 .
.




Next: Invariantie van de lichtsnelheid
Up: De speciale relativiteitstheorie
Previous: Lorentzcontractie
Contents
Jo van den Brand
2009-01-31
![]() ,
,
![]() ,
,
![]() de volgende vergelijking
oplossen,
de volgende vergelijking
oplossen,
![]() ) niet te beschouwen. In dat
geval moet voldaan worden aan
) niet te beschouwen. In dat
geval moet voldaan worden aan
![]() en
en ![]() ). In dat geval dient de transformatie te voldoen aan
). In dat geval dient de transformatie te voldoen aan
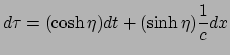
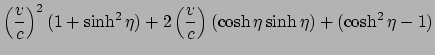
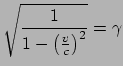
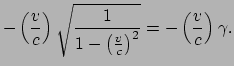
![]() door
door ![]() te vervangen. We vinden
te vervangen. We vinden
![]() ten opzichte van elkaar. Twee specifieke voorbeelden van zulke relaties
hadden we al eerder gezien, toen nog direct afgeleid uit het minkowskilijnelement:
de tijddilatatie en de lorentzcontractie. Deze liggen dan ook automatisch opgesloten
in de lorentztransformaties. Voor tijddilatatie hoeven we alleen maar te kijken
naar het speciale geval dat een van de waarnemers een tijdsduur meet tussen
twee gebeurtenissen die ten opzichte van hem op een en dezelfde positie plaatsvinden,
zodat
ten opzichte van elkaar. Twee specifieke voorbeelden van zulke relaties
hadden we al eerder gezien, toen nog direct afgeleid uit het minkowskilijnelement:
de tijddilatatie en de lorentzcontractie. Deze liggen dan ook automatisch opgesloten
in de lorentztransformaties. Voor tijddilatatie hoeven we alleen maar te kijken
naar het speciale geval dat een van de waarnemers een tijdsduur meet tussen
twee gebeurtenissen die ten opzichte van hem op een en dezelfde positie plaatsvinden,
zodat ![]() ; voor deze waarnemer schrijven we
; voor deze waarnemer schrijven we
![]() ;
er volgt dan direct uit vergelijking (194)
dat een andere waarnemer een tijdsduur meet tussen
deze twee gebeurtenissen gelijk aan
;
er volgt dan direct uit vergelijking (194)
dat een andere waarnemer een tijdsduur meet tussen
deze twee gebeurtenissen gelijk aan
![]() . Dit is precies de
tijddilatatieformule in vergelijking (172).
Verder, om de lorentzcontractie af te leiden uit
de lorentztransformaties hoeft alleen naar het speciale geval gekeken te worden
dat de twee gebeurtenissen de metingen zijn van voor- en achterkant van een lat
door een waarnemer die deze metingen doet op een en hetzelfde tijdstip (immers:
als dat niet het geval is, zal de lat `voorbij' vliegen in de tijd die deze waarnemer
wacht tussen meting van voor- en achterkant, en stelt de afstand tussen gemeten
positie van voor- en achterkant dus niet meer de lengte van de lat voor). Voor
deze waarnemer geldt dan ook
. Dit is precies de
tijddilatatieformule in vergelijking (172).
Verder, om de lorentzcontractie af te leiden uit
de lorentztransformaties hoeft alleen naar het speciale geval gekeken te worden
dat de twee gebeurtenissen de metingen zijn van voor- en achterkant van een lat
door een waarnemer die deze metingen doet op een en hetzelfde tijdstip (immers:
als dat niet het geval is, zal de lat `voorbij' vliegen in de tijd die deze waarnemer
wacht tussen meting van voor- en achterkant, en stelt de afstand tussen gemeten
positie van voor- en achterkant dus niet meer de lengte van de lat voor). Voor
deze waarnemer geldt dan ook ![]() , en zal de lengte van de lat gegeven zijn
door
, en zal de lengte van de lat gegeven zijn
door ![]() ; volgens vergelijking (194)
meet de waarnemer in rust ten opzichte van de lat een
lengte van
; volgens vergelijking (194)
meet de waarnemer in rust ten opzichte van de lat een
lengte van
![]() . Dit is
precies de lorentzcontractie formule, vergelijking (177).
. Dit is
precies de lorentzcontractie formule, vergelijking (177).
![]() .
.