



Next: Vectorveld
Up: Geometrische objecten
Previous: Curve
Contents
We beschouwen enkel differentieerbare
variëteiten en dat zijn ruimten die continu en differentieerbaar zijn.
Dit betekent dat we op elk punt van de variëteit een scalairveld
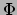 kunnen definiëren en dat deze functie overal kan worden
gedifferentieerd.
kunnen definiëren en dat deze functie overal kan worden
gedifferentieerd.
Figuur:
Grafische voorstelling van een differentieerbare variëteit
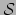 .
Binnen een lokaal gebied kan een kaart met gladde (reële getallen) coördinaten
.
Binnen een lokaal gebied kan een kaart met gladde (reële getallen) coördinaten 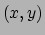 de punten in de variëteit labelen. Om de hele variëteit te bestrijken dienen
we verschillende kaarten samen te `lijmen'.
de punten in de variëteit labelen. Om de hele variëteit te bestrijken dienen
we verschillende kaarten samen te `lijmen'.
|
|
Stel we hebben een gladde functie 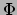 gedefinieerd op
gedefinieerd op
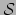 , denk
bijvoorbeeld aan de temperatuur op het aardoppervlak. In moderne wiskundige
taal is
, denk
bijvoorbeeld aan de temperatuur op het aardoppervlak. In moderne wiskundige
taal is 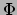 dan een gladde afbeelding van
dan een gladde afbeelding van
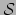 naar de ruimte
van reële getallen
naar de ruimte
van reële getallen
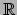 , omdat
, omdat 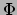 aan ieder punt van
aan ieder punt van
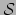 een reëel getal toekent, dit wil zeggen
een reëel getal toekent, dit wil zeggen 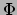 maakt
een afbeelding van
maakt
een afbeelding van
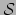 naar de reële getallen. Een
dergelijke functie wordt vaak een scalairveld op
naar de reële getallen. Een
dergelijke functie wordt vaak een scalairveld op
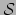 genoemd.
Binnen een bepaald lokaal gebied heeft
genoemd.
Binnen een bepaald lokaal gebied heeft 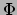 een coördinatenvergelijking
een coördinatenvergelijking
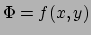 op de bijbehorende kaart. De gladheid van het scalairveld
op de bijbehorende kaart. De gladheid van het scalairveld
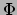 komt dan tot uitdrukking in de differentieerbaarheid
van de functie
komt dan tot uitdrukking in de differentieerbaarheid
van de functie 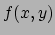 . Het zal de lezer opgevallen zijn dat onderscheid
wordt gemaakt tussen
. Het zal de lezer opgevallen zijn dat onderscheid
wordt gemaakt tussen 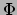 en
en 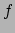 . De reden is dat
. De reden is dat 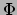 gedefinieerd
is op het oppervlak, maar uitgedrukt kan worden in verschillende
coördinatensystemen. De wiskundige uitdrukking voor
gedefinieerd
is op het oppervlak, maar uitgedrukt kan worden in verschillende
coördinatensystemen. De wiskundige uitdrukking voor 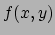 kan
verschillen voor verschillende kaarten, terwijl de grootheid
kan
verschillen voor verschillende kaarten, terwijl de grootheid 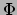 op elk specifiek punt van het oppervlak bestreken door deze kaarten
niet verandert. Voor een andere kaart in Fig. 33
geldt bijvoorbeeld
op elk specifiek punt van het oppervlak bestreken door deze kaarten
niet verandert. Voor een andere kaart in Fig. 33
geldt bijvoorbeeld
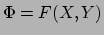 . Als de kaarten overlappen geldt
. Als de kaarten overlappen geldt
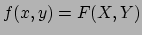 . De specifieke uitdrukking voor
. De specifieke uitdrukking voor 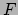 , in termen
van
, in termen
van 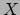 en
en 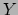 , zal in het algemeen verschillen van de uitdrukking
voor
, zal in het algemeen verschillen van de uitdrukking
voor 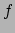 in termen van
in termen van 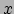 en
en 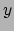 . In het algemeen is
. In het algemeen is 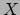 een
gecompliceerde functie van
een
gecompliceerde functie van 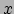 en
en 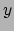 in het overlap gebied,
en dat geldt ook voor
in het overlap gebied,
en dat geldt ook voor 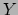 . Met deze functies dienen we rekening
te houden als we van
. Met deze functies dienen we rekening
te houden als we van 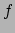 naar
naar 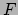 gaan. Dergelijke functies, die de
coördinaten van één systeem beschrijven in termen van die
van het andere systeem,
gaan. Dergelijke functies, die de
coördinaten van één systeem beschrijven in termen van die
van het andere systeem,
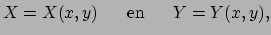 |
(91) |
en hun inverse
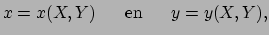 |
(92) |
noemen we overgangsfuncties.
Teneinde het bovenstaande concreet te maken, stelt U zich de volgende
situatie voor. Een waarnemer die we voorzien van het label
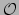 besluit om de temperatuur van een bepaald gebiedje van het aardoppervlak
in kaart te brengen. Hiertoe maakt hij een kaart van het gebied en
gebruikt hij coördinaten
besluit om de temperatuur van een bepaald gebiedje van het aardoppervlak
in kaart te brengen. Hiertoe maakt hij een kaart van het gebied en
gebruikt hij coördinaten 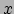 en
en 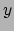 . Een bepaald punt
. Een bepaald punt
 van het aardoppervlak komt overeen met een bepaald punt
van het aardoppervlak komt overeen met een bepaald punt 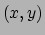 op zijn
kaart. Een tweede waarnemer (die we labelen met
op zijn
kaart. Een tweede waarnemer (die we labelen met
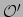 ) komt
op hetzelfde idee. Hij maakt ook een kaart, echter met volledig andere
coördinaten
) komt
op hetzelfde idee. Hij maakt ook een kaart, echter met volledig andere
coördinaten
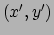 . Na verloop van tijd
besluiten beide waarnemers om hun analyse te vergelijken en leggen ze
de kaarten naast elkaar. Het blijkt mogelijk om een wiskundige
transformatie33
te vinden tussen punten
. Na verloop van tijd
besluiten beide waarnemers om hun analyse te vergelijken en leggen ze
de kaarten naast elkaar. Het blijkt mogelijk om een wiskundige
transformatie33
te vinden tussen punten 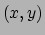 op de kaart van waarnemer
op de kaart van waarnemer
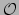 en
en
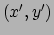 van
van
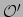 .
De transformatie correspondeert met de volgende set lineaire vergelijkingen,
.
De transformatie correspondeert met de volgende set lineaire vergelijkingen,
Deze vergelijkingen definiëren een lineaire transformatie34
(of lineaire afbeelding) van een
punt 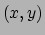 naar een corresponderend beeld
naar een corresponderend beeld
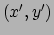 .
In matrixvorm mogen we dit schrijven als
.
In matrixvorm mogen we dit schrijven als
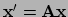 ,
en indien de afbeelding bijectief (een-op-een afbeelding)
is, geldt
,
en indien de afbeelding bijectief (een-op-een afbeelding)
is, geldt
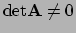 .
Er is altijd sprake van een alias-alibi aspect bij dergelijke
transformaties: als
.
Er is altijd sprake van een alias-alibi aspect bij dergelijke
transformaties: als
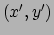 wordt beschouwd als
het definiëren van nieuwe coördinaten (een nieuwe naam) voor
wordt beschouwd als
het definiëren van nieuwe coördinaten (een nieuwe naam) voor 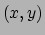 ,
dan hebben we te maken met het alias aspect; als
,
dan hebben we te maken met het alias aspect; als
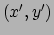 beschouwd wordt als een nieuwe positie (plaats) voor
beschouwd wordt als een nieuwe positie (plaats) voor 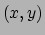 , dan komt
het alibi aspect te voorschijn. In tensorrekening zijn we in het algemeen
meer geïnteresseerd in het alias aspect. We noemen de twee coördinatenstelsels
gerelateerd door
, dan komt
het alibi aspect te voorschijn. In tensorrekening zijn we in het algemeen
meer geïnteresseerd in het alias aspect. We noemen de twee coördinatenstelsels
gerelateerd door
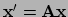 respectievelijk het systeem
respectievelijk het systeem
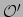 en
en
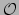 . Stel dat het punt
. Stel dat het punt
 van de variëteit in het systeem
van de variëteit in het systeem
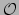 gegeven wordt door
de coördinaten
gegeven wordt door
de coördinaten
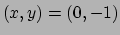 . Met vergelijking (99)
vinden voor het punt
. Met vergelijking (99)
vinden voor het punt
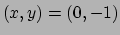 het beeldpunt
het beeldpunt
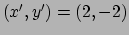 in systeem
in systeem
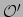 .
Het origineel in
.
Het origineel in
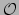 en het beeldpunt in
en het beeldpunt in
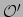 hebben verschillende coördinaten,
maar stellen hetzelfde punt
hebben verschillende coördinaten,
maar stellen hetzelfde punt
 in de variëteit voor.
in de variëteit voor.
Stel dat waarnemer
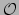 de temperatuur
de temperatuur 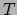 in zijn coördinatenstelsel kan
beschrijven met uitdrukking
in zijn coördinatenstelsel kan
beschrijven met uitdrukking
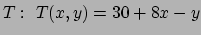 (dit is een scalairveld
(dit is een scalairveld 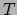 dat verschillende waarden kan aannemen op verschillende punten).
Op punt
dat verschillende waarden kan aannemen op verschillende punten).
Op punt
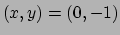 wordt de temperatuur
dan gegeven door
wordt de temperatuur
dan gegeven door
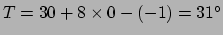 C. Om de corresponderende uitdrukking
voor de andere waarnemer, die in
coördinatenstelsel
C. Om de corresponderende uitdrukking
voor de andere waarnemer, die in
coördinatenstelsel
 , te vinden, dienen we eerst de inverse
transformatie gegeven door vergelijking (99) af te leiden. Hiertoe inverteren
we de bijbehorende matrix en vinden
, te vinden, dienen we eerst de inverse
transformatie gegeven door vergelijking (99) af te leiden. Hiertoe inverteren
we de bijbehorende matrix en vinden
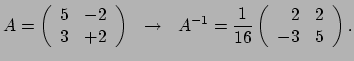 |
(94) |
Er geldt dan
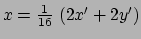 en
en
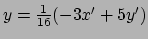 en
we krijgen een andere uitdrukking voor de temperatuur. We vinden
en
we krijgen een andere uitdrukking voor de temperatuur. We vinden
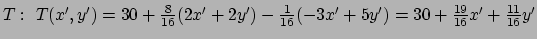 .
Als we nu weer naar de temperatuur op hetzelfde punt (beeldpunt
.
Als we nu weer naar de temperatuur op hetzelfde punt (beeldpunt
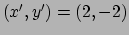 ) kijken,
vinden we weer
) kijken,
vinden we weer
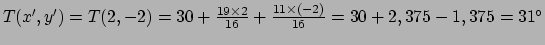 C, zoals het hoort, want de temperatuur
is een scalairveld dat zich niets aantrekt van het coördinatenstelsel
dat we kiezen. Beide waarnemers zijn het eens: in de variëteit (het stukje
aardoppervlak waar de kaarten overlappen in dit geval) is de temperatuur op punt
C, zoals het hoort, want de temperatuur
is een scalairveld dat zich niets aantrekt van het coördinatenstelsel
dat we kiezen. Beide waarnemers zijn het eens: in de variëteit (het stukje
aardoppervlak waar de kaarten overlappen in dit geval) is de temperatuur op punt
 gelijk aan
gelijk aan 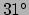 C.
C.




Next: Vectorveld
Up: Geometrische objecten
Previous: Curve
Contents
Jo van den Brand
2009-01-31
![]() kunnen definiëren en dat deze functie overal kan worden
gedifferentieerd.
kunnen definiëren en dat deze functie overal kan worden
gedifferentieerd.
![\includegraphics[width=12cm]{Figures/manifold.eps}](img636.png)
![]() besluit om de temperatuur van een bepaald gebiedje van het aardoppervlak
in kaart te brengen. Hiertoe maakt hij een kaart van het gebied en
gebruikt hij coördinaten
besluit om de temperatuur van een bepaald gebiedje van het aardoppervlak
in kaart te brengen. Hiertoe maakt hij een kaart van het gebied en
gebruikt hij coördinaten ![]() en
en ![]() . Een bepaald punt
. Een bepaald punt
![]() van het aardoppervlak komt overeen met een bepaald punt
van het aardoppervlak komt overeen met een bepaald punt ![]() op zijn
kaart. Een tweede waarnemer (die we labelen met
op zijn
kaart. Een tweede waarnemer (die we labelen met
![]() ) komt
op hetzelfde idee. Hij maakt ook een kaart, echter met volledig andere
coördinaten
) komt
op hetzelfde idee. Hij maakt ook een kaart, echter met volledig andere
coördinaten
![]() . Na verloop van tijd
besluiten beide waarnemers om hun analyse te vergelijken en leggen ze
de kaarten naast elkaar. Het blijkt mogelijk om een wiskundige
transformatie33
te vinden tussen punten
. Na verloop van tijd
besluiten beide waarnemers om hun analyse te vergelijken en leggen ze
de kaarten naast elkaar. Het blijkt mogelijk om een wiskundige
transformatie33
te vinden tussen punten ![]() op de kaart van waarnemer
op de kaart van waarnemer
![]() en
en
![]() van
van
![]() .
De transformatie correspondeert met de volgende set lineaire vergelijkingen,
.
De transformatie correspondeert met de volgende set lineaire vergelijkingen,
![]() de temperatuur
de temperatuur ![]() in zijn coördinatenstelsel kan
beschrijven met uitdrukking
in zijn coördinatenstelsel kan
beschrijven met uitdrukking
![]() (dit is een scalairveld
(dit is een scalairveld ![]() dat verschillende waarden kan aannemen op verschillende punten).
Op punt
dat verschillende waarden kan aannemen op verschillende punten).
Op punt
![]() wordt de temperatuur
dan gegeven door
wordt de temperatuur
dan gegeven door
![]() C. Om de corresponderende uitdrukking
voor de andere waarnemer, die in
coördinatenstelsel
C. Om de corresponderende uitdrukking
voor de andere waarnemer, die in
coördinatenstelsel
![]() , te vinden, dienen we eerst de inverse
transformatie gegeven door vergelijking (99) af te leiden. Hiertoe inverteren
we de bijbehorende matrix en vinden
, te vinden, dienen we eerst de inverse
transformatie gegeven door vergelijking (99) af te leiden. Hiertoe inverteren
we de bijbehorende matrix en vinden