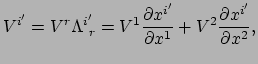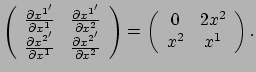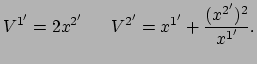Next: Lineaire functionaal, 1-vorm of
Up: Geometrische objecten
Previous: Scalairveld
Contents
Het begrip vector is ontstaan in de fysica en wel door begrippen als
snelheid en versnelling. Deze objecten hebben een grootte
en een richting en ze kunnen worden opgeteld en met een reëel getal
vermenigvuldigd.
Veel verwarring komt voort uit het feit dat de naam `vector' refereert
naar twee verschillende concepten: enerzijds een zuiver numeriek object
(een rij of kolom getallen) en anderzijds een object met geometrische
of topologische eigenschappen. In deze laatste betekenis is de vector
onafhankelijk van het referentiesysteem en heeft daarom geen unieke
decompositie in numerieke elementen. We benadrukken het om een vector
(of meer algemeen een tensor)
te zien als een `geometrisch object', iets dat men zich kan voorstellen
zonder te moeten refereren naar een specifiek referentiesysteem.
Figuur:
Grafische voorstelling van een vectorveld als een
`verdeling van pijltjes over de variëteit' getekend op
 .
De vectoren zijn gebonden aan hun plaats.
.
De vectoren zijn gebonden aan hun plaats.
|
|
Fig. 34 geeft een voorstelling van een vectorveld,
bijvoorbeeld de horizontale windsnelheid op het oppervlak van de aarde.
Een topologische vector is een object  dat leeft in een bepaalde ruimte,
in ons voorbeeld van het aardoppervlak is dat een niet-euclidische twee-dimensionale ruimte met
constante positieve kromming35. De vector heeft een bepaalde betekenis
in die ruimte en stelt in ons voorbeeld de horizontale windsnelheid
op het oppervlak van de aarde voor.
We kunnen vectoren tekenen als pijltjes, zonder
te refereren naar een bepaalde basis, en dat hebben we gedaan in
Fig. 34.
dat leeft in een bepaalde ruimte,
in ons voorbeeld van het aardoppervlak is dat een niet-euclidische twee-dimensionale ruimte met
constante positieve kromming35. De vector heeft een bepaalde betekenis
in die ruimte en stelt in ons voorbeeld de horizontale windsnelheid
op het oppervlak van de aarde voor.
We kunnen vectoren tekenen als pijltjes, zonder
te refereren naar een bepaalde basis, en dat hebben we gedaan in
Fig. 34.
Er is geen unieke manier om een topologische
vector te expanderen in termen van componenten. Zonder verdere
informatie is een statement als
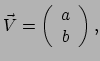 |
(95) |
zonder enige betekenis, omdat we niet weten welke basis we dienen te gebruiken.
Wat we dienen te doen is iets te schrijven als
![$\displaystyle \vec V \xrightarrow[ \mathcal{O} ]{}
\left( \begin{array}{c}
a \\
b \\
\end{array}
\right),$](img664.png) |
(96) |
waarmee we met het pijltje
![$ \xrightarrow[ O ]{}$](img665.png) bedoelen dat de vector
bedoelen dat de vector  componenten
componenten 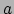 en
en 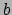 heeft, die gegeven zijn in het referentiesysteem van
waarnemer
heeft, die gegeven zijn in het referentiesysteem van
waarnemer
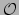 (bijvoorbeeld het
(bijvoorbeeld het 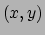 systeem).
De vector
systeem).
De vector  is een pijl met als componenten een verzameling van
coördinatenstelsel afhankelijke getallen. We kunnen ook schrijven
is een pijl met als componenten een verzameling van
coördinatenstelsel afhankelijke getallen. We kunnen ook schrijven
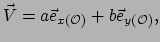 |
(97) |
waarbij
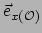 en
en
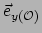 de basisvectoren in het
referentiesysteem van waarnemer
de basisvectoren in het
referentiesysteem van waarnemer
 zijn. We hadden net zo goed
een andere waarnemer kunnen kiezen, bijvoorbeeld
zijn. We hadden net zo goed
een andere waarnemer kunnen kiezen, bijvoorbeeld
 ,
en dan geldt
,
en dan geldt
![$\displaystyle \vec V \xrightarrow[ {\mathcal{O}}^\prime ]{}
\left( \begin{array}{c}
p \\
q \\
\end{array}
\right) ,$](img670.png) |
(98) |
waarbij
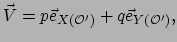 |
(99) |
met
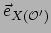 en
en
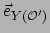 de basisvectoren in het
referentiesysteem van waarnemer
de basisvectoren in het
referentiesysteem van waarnemer
 (bijvoorbeeld het
(bijvoorbeeld het  systeem).
Merk op dat vergelijkingen
(102) - (105) alle geldige beschrijvingen zijn van
dezelfde topologische vector
systeem).
Merk op dat vergelijkingen
(102) - (105) alle geldige beschrijvingen zijn van
dezelfde topologische vector  .
.
Het verleidelijk om te denken dat het symbool 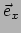 de
de 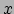 -component van
de
-component van
de 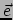 -vector voorstelt. We bedoelen echter met
-vector voorstelt. We bedoelen echter met 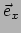 een volledige vector,
waarbij het subscript
een volledige vector,
waarbij het subscript 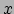 onderdeel is van de naam van de vector en aangeeft
welke van de basisvectoren we bedoelen (namelijk de basisvector in de
onderdeel is van de naam van de vector en aangeeft
welke van de basisvectoren we bedoelen (namelijk de basisvector in de 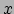 -richting).
De vector
-richting).
De vector 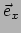 heeft zelf componenten, waarvan de
heeft zelf componenten, waarvan de 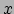 -component geschreven
kan worden als
-component geschreven
kan worden als
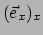 . De volledige basis36
geven we in dit geval aan met {
. De volledige basis36
geven we in dit geval aan met {
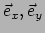 }.
}.
Elke complete set vectoren kan gebruikt worden als basis. In Fig. 33
zijn de referentiesystemen van drie waarnemers weergegeven. Een topologische
vector wordt voorgesteld door de pijl (zie Fig. 34) en hoort niet bij een of
ander referentiesysteem. Het is een topologisch object met zelfstandig bestaansrecht.
De waarnemers bekijken het echter vanuit hun eigen gezichtspunt (referentiesysteem).
Cruciaal is te begrijpen dat de vector niet verandert als we van het ene naar
het andere referentiesysteem gaan. Er geldt
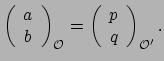 |
(100) |
Natuurlijk zijn de componenten 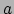 en
en 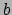 niet gelijk aan
niet gelijk aan 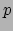 en
en 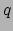 en
dienen we een voorschrift te vinden hoe we deze kunnen berekenen als we van
basis veranderen. We gaan als volgt te werk: kies eerst een
puntgebeurtenis
en
dienen we een voorschrift te vinden hoe we deze kunnen berekenen als we van
basis veranderen. We gaan als volgt te werk: kies eerst een
puntgebeurtenis
 . Op deze puntgebeurtenis kiezen we
dan een complete set onafhankelijke vectoren (hierbij is elke
redelijke keuze geoorloofd). We noemen deze vectoren
. Op deze puntgebeurtenis kiezen we
dan een complete set onafhankelijke vectoren (hierbij is elke
redelijke keuze geoorloofd). We noemen deze vectoren 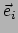 en gebruiken
deze als basis om andere vectoren op punt
en gebruiken
deze als basis om andere vectoren op punt
 in te expanderen:
in te expanderen:
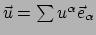 en
en
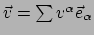 .
.
Figuur 35:
De basisvectoren die door een coördinatensysteem worden geïnduceerd,
vormen een tangentenruimte op elke gebeurtenis van de variëteit.
|
|
Fig. 35 toont deze basis een tangentenruimte  definieert op punt
definieert op punt
 .
Alle vectoren worden lokaal op dit punt worden beschreven37.
De richtingsafgeleiden
.
Alle vectoren worden lokaal op dit punt worden beschreven37.
De richtingsafgeleiden
 langs deze basisvectoren spannen de tangentenruimte (de raakruimte in
punt
langs deze basisvectoren spannen de tangentenruimte (de raakruimte in
punt
 op. In Fig. 35 hebben we als coördinaten
op. In Fig. 35 hebben we als coördinaten
 en
en
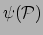 gebruikt. De basisvectoren
worden gegeven door de richtingsafgeleiden langs de coördinaatlijnen
en zijn
gebruikt. De basisvectoren
worden gegeven door de richtingsafgeleiden langs de coördinaatlijnen
en zijn
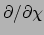 en
en
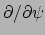 . We kunnen
een vector dus zien als een richtingsafgeleide. We zien dat deze vectoren
niet in de variëteit liggen, maar een eigen vectorruimte opspannen.
Alhoewel Fig. 35 een inzichtelijke voorstelling geeft, dienen
we ons te realiseren, dat een abstracte variëteit beschouwd dient te
worden als een zelfstandige entiteit: er is geen hogere-dimensionele
ruimte waarin de variëteit en zijn tangentenruimten zijn ingebed.
We geven een toelichting aan de hand
van een voorbeeld dat de gang van zaken in de vertrouwde drie-dimensionale
euclidische ruimte beschrijft.
. We kunnen
een vector dus zien als een richtingsafgeleide. We zien dat deze vectoren
niet in de variëteit liggen, maar een eigen vectorruimte opspannen.
Alhoewel Fig. 35 een inzichtelijke voorstelling geeft, dienen
we ons te realiseren, dat een abstracte variëteit beschouwd dient te
worden als een zelfstandige entiteit: er is geen hogere-dimensionele
ruimte waarin de variëteit en zijn tangentenruimten zijn ingebed.
We geven een toelichting aan de hand
van een voorbeeld dat de gang van zaken in de vertrouwde drie-dimensionale
euclidische ruimte beschrijft.
Voorbeeld: coördinatensysteem in euclidische ruimte
We beschouwen de euclidische ruimte met cartesische coördinaten 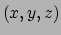 en de bijbehorende basis van eenheidsvectoren
en de bijbehorende basis van eenheidsvectoren
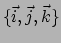 .
We gebruiken dit systeem als algemene referentie om andere, niet cartesische
coördinaten in te beschrijven.
We hebben een tweede coördinatensysteem
.
We gebruiken dit systeem als algemene referentie om andere, niet cartesische
coördinaten in te beschrijven.
We hebben een tweede coördinatensysteem 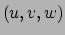 dat niet cartesisch is,
bijvoorbeeld de sferische coördinaten
dat niet cartesisch is,
bijvoorbeeld de sferische coördinaten
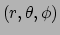 . Er geldt
. Er geldt
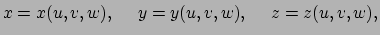 |
(101) |
en we kunnen dit inverteren om 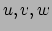 te schrijven in termen van
te schrijven in termen van 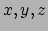 .
We kunnen bovenstaande vergelijking schrijven als
.
We kunnen bovenstaande vergelijking schrijven als
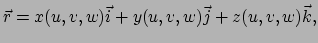 |
(102) |
Indien we 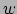 gelijk zetten aan de constante
gelijk zetten aan de constante 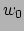 , terwijl
, terwijl 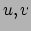 mogen
variëren, krijgen we
mogen
variëren, krijgen we
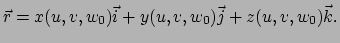 |
(103) |
hetgeen een parametrische vergelijking is voor het coördinatenoppervlak
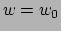 , waarbij de coördinaten
, waarbij de coördinaten 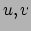 de rol van parameters spelen.
We kunnen de parametrische vergelijkingen voor de twee andere oppervlakken
op identieke wijze verkrijgen. Als we in bovenstaande vergelijking
de rol van parameters spelen.
We kunnen de parametrische vergelijkingen voor de twee andere oppervlakken
op identieke wijze verkrijgen. Als we in bovenstaande vergelijking
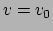 en
en 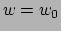 stellen, maar
stellen, maar 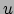 laten variëren, krijgen we
laten variëren, krijgen we
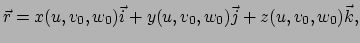 |
(104) |
krijgen we een parametrische vergelijking voor de coördinatencurve
gegeven door de snijlijn van vlakken 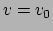 en
en 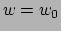 , waarbij
, waarbij 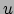 de rol van parameter langs de curve speelt.
We kunnen de parametrische vergelijkingen voor de twee andere curven
op identieke wijze verkrijgen.
de rol van parameter langs de curve speelt.
We kunnen de parametrische vergelijkingen voor de twee andere curven
op identieke wijze verkrijgen.
Figuur 36:
De coördinaatoppervlakken (bol, kegel en halfruimte)
en coördinaatcurven voor sferische coördinaten.
|
|
Door elk punt
 met coördinaten
met coördinaten
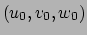 gaan drie
coördinaatvlakken gegeven door
gaan drie
coördinaatvlakken gegeven door 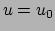 ,
, 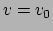 en
en 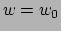 . De
vlakken snijden elkaar in coördinaatcurven. Voor sferische
coördinaten hebben we
. De
vlakken snijden elkaar in coördinaatcurven. Voor sferische
coördinaten hebben we
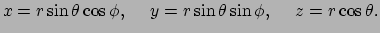 |
(105) |
waarbij de coördinaten het volgende bereik hebben: 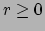 ,
,
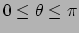 en
en
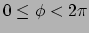 .
Fig. 36
toont dat het coördinaatvlak
.
Fig. 36
toont dat het coördinaatvlak 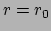 een bol is met straal
een bol is met straal 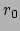 ,
het coördinaatvlak
,
het coördinaatvlak
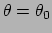 is een oneindige kegel met de apex
in de oorsprong en de as verticaal, en het coördinaatvlak
is een oneindige kegel met de apex
in de oorsprong en de as verticaal, en het coördinaatvlak
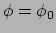 is een
half-oneindig vlak met de
is een
half-oneindig vlak met de 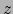 -as als rand.
-as als rand.
De oppervlakken
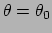 en
en
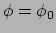 snijden elkaar en dat
resulteert in de coördinaatcurve die een deellijn is die vanaf
snijden elkaar en dat
resulteert in de coördinaatcurve die een deellijn is die vanaf  vertrekt
door
vertrekt
door
 gaat; de oppervlakken
gaat; de oppervlakken
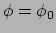 en
en 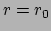 snijden
elkaar in de curve die een halve cirkel is met eindpunten op de
snijden
elkaar in de curve die een halve cirkel is met eindpunten op de 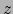 -as en
die door
-as en
die door
 gaat; en de oppervlakken
gaat; en de oppervlakken 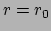 en
en
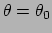 snijden elkaar in de horizontale cirkel door
snijden elkaar in de horizontale cirkel door
 met het middelpunt
op de
met het middelpunt
op de 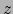 -as.
-as.
Als we vergelijking (110) differentiëren naar de parameter 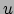 ,
krijgen we een tangentenvector aan de coördinaatcurve. Omdat we tijdens
differentiëren
,
krijgen we een tangentenvector aan de coördinaatcurve. Omdat we tijdens
differentiëren 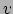 en
en 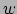 constant houden (want op deze wijze was de
curve gedefinieerd), hebben we in feite de partiële afgeleide
naar
constant houden (want op deze wijze was de
curve gedefinieerd), hebben we in feite de partiële afgeleide
naar 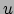 genomen van vergelijking (107). Als we op dezelfde
manier vergelijking (107) partieel afleiden naar
genomen van vergelijking (107). Als we op dezelfde
manier vergelijking (107) partieel afleiden naar 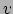 en
en 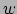 ,
krijgen we de tangentenvectoren van de andere twee coördinaatcurven.
De drie partiële afgeleiden
,
krijgen we de tangentenvectoren van de andere twee coördinaatcurven.
De drie partiële afgeleiden
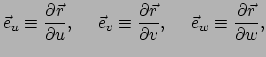 |
(106) |
berekend op punt
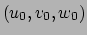 geven tangentenvectoren aan de drie
coördinaatcurven die door
geven tangentenvectoren aan de drie
coördinaatcurven die door
 gaan. Op deze wijze
verkrijgen we de natuurlijke basis
gaan. Op deze wijze
verkrijgen we de natuurlijke basis
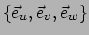 op punt
op punt
 . In het algemeen is deze basis niet orthogonaal
en zijn de vectoren geen eenheidsvectoren.
. In het algemeen is deze basis niet orthogonaal
en zijn de vectoren geen eenheidsvectoren.
Gegeven een vectorveld
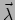 , kunnen we in elk punt
, kunnen we in elk punt
 de vector
de vector
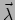 refereren aan basis
refereren aan basis
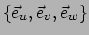 ,
,
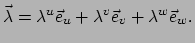 |
(107) |
We gebruiken 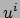
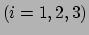 in plaats van
in plaats van 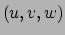 voor de coördinaten,
en
voor de coördinaten,
en
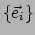
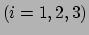 in plaats van
in plaats van
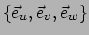 voor de natuurlijke basis. Voor een vector
voor de natuurlijke basis. Voor een vector
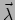 duiden we
de componenten in de basis
duiden we
de componenten in de basis
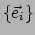 aan met
aan met 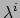
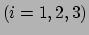 .
We kunnen vergelijking (113) nu uitdrukken als
.
We kunnen vergelijking (113) nu uitdrukken als
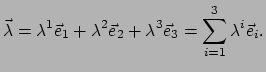 |
(108) |
We spreken nu af dat een index uit het midden van het alfabet (
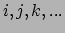 )
altijd loopt over de waarden 1,2 en 3. Verder sommeren we automatisch
als dezelfde index voorkomt als superscript en subscript (dit heet de
sommatieconventie van Einstein). We kunnen vergelijking (114)
nu schrijven als
)
altijd loopt over de waarden 1,2 en 3. Verder sommeren we automatisch
als dezelfde index voorkomt als superscript en subscript (dit heet de
sommatieconventie van Einstein). We kunnen vergelijking (114)
nu schrijven als
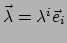 .
Merk op dat de twee indices die op deze wijze gebruikt worden
dummie indices genoemd worden en vervangen mogen worden door andere
letters (die nog niet in gebruik zijn).
.
Merk op dat de twee indices die op deze wijze gebruikt worden
dummie indices genoemd worden en vervangen mogen worden door andere
letters (die nog niet in gebruik zijn).
In het volgende bestuderen we viervectoren in ruimtetijd.
Een typische vector is de verplaatsingsvector
![$ \Delta \vec x \xrightarrow[ \mathcal{O} ]{} (\Delta t, \Delta x, \Delta y, \Delta z)$](img728.png) .
Een andere notatie is
.
Een andere notatie is
![$ \Delta \vec x \xrightarrow[ \mathcal{O} ]{} \left\{ \Delta x^\alpha \right\}$](img729.png) . Als we
willen weten wat de componenten van deze vector zijn in een ander coördinatenstelsel,
bijvoorbeeld het systeem
. Als we
willen weten wat de componenten van deze vector zijn in een ander coördinatenstelsel,
bijvoorbeeld het systeem
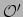 , dan schrijven we
, dan schrijven we
![$ \Delta \vec x \xrightarrow[ {\mathcal{O}}^\prime ]{} \left\{ \Delta x^{\alpha^\prime} \right\}$](img730.png) .
We gebruiken het accent boven de index om de nieuwe coördinaten aan te geven. De
vector
.
We gebruiken het accent boven de index om de nieuwe coördinaten aan te geven. De
vector
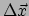 is hetzelfde en daarvoor hebben we geen nieuwe notatie nodig
als we van referentiesysteem veranderen. We kunnen de nieuwe componenten
is hetzelfde en daarvoor hebben we geen nieuwe notatie nodig
als we van referentiesysteem veranderen. We kunnen de nieuwe componenten
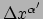 vinden met behulp van de transformatiematrix van
het ene naar het andere systeem (zie vergelijking (88)) en we
schrijven
vinden met behulp van de transformatiematrix van
het ene naar het andere systeem (zie vergelijking (88)) en we
schrijven
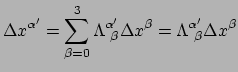 |
(109) |
voor willekeurige
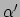 . De verzameling
. De verzameling
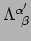 bestaat uit 16 getallen die de transformatiematrix vertegenwoordigen.
De notatie maakt weer gebruik van Einstein's sommatieconventie en vergelijking
(115) stelt eigenlijk vier verschillende vergelijkingen voor
(
bestaat uit 16 getallen die de transformatiematrix vertegenwoordigen.
De notatie maakt weer gebruik van Einstein's sommatieconventie en vergelijking
(115) stelt eigenlijk vier verschillende vergelijkingen voor
(
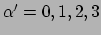 ).
).
Een algemene vector (wij zijn geïnteresseerd in viervectoren) is gedefinieerd
als een verzameling getallen (de componenten van de vector ten opzichte van
een bepaalde basis,
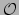 ) als
) als
![$ \vec V \xrightarrow[ \mathcal{O} ]{} (V^0, V^1, V^2, V^3) = \left\{ V^\alpha \right\}$](img736.png) en door de regel dat zijn componenten in een systeem
en door de regel dat zijn componenten in een systeem
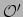 gegeven worden door
gegeven worden door
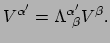 |
(110) |
Dus de componenten van een vector (vergelijking (116))
transformeren op dezelfde manier als de coördinaten (vergelijking (115)).
De componenten 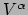 van een vector
van een vector  ten opzichte
van de natuurlijke basis
ten opzichte
van de natuurlijke basis
 worden de
contravariante componenten genoemd. Een object waarvan de componenten
contravariant transformeren, een vector, noemen we een
worden de
contravariante componenten genoemd. Een object waarvan de componenten
contravariant transformeren, een vector, noemen we een
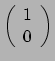 tensor.
Stel dat we twee systemen met curvelineaire coördinaten hebben
in ruimtetijd, aangegeven met
tensor.
Stel dat we twee systemen met curvelineaire coördinaten hebben
in ruimtetijd, aangegeven met
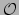 en
en
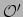 . We vragen ons af hoe
de contravariante componenten van een vector veranderen als we
van het ene naar het andere systeem gaan. We noemen
. We vragen ons af hoe
de contravariante componenten van een vector veranderen als we
van het ene naar het andere systeem gaan. We noemen
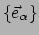 de basis in het systeem van waarnemer
de basis in het systeem van waarnemer
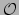 en
en
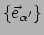 de basis in het systeem van waarnemer
de basis in het systeem van waarnemer
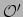 .
Er geldt
.
Er geldt
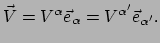 |
(111) |
We kunnen bovenstaande relatie gebruiken om de transformatiewet voor de basisvectoren
te vinden, dit wil zeggen de relatie tussen
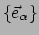 en
en
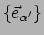 . Met vergelijking (116)
kunnen we vergelijking (117) schrijven als
. Met vergelijking (116)
kunnen we vergelijking (117) schrijven als
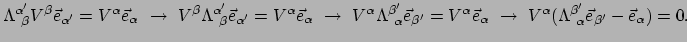 |
(112) |
In de eerste stap maken we gebruik van het feit dat
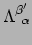 en
en 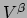 gewoon getallen zijn, en dat hun volgorde in een eindige som niet uitmaakt.
In de tweede stap gebruiken we het feit dat
gewoon getallen zijn, en dat hun volgorde in een eindige som niet uitmaakt.
In de tweede stap gebruiken we het feit dat 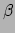 en
en
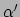 dummie
indices zijn: we veranderen
dummie
indices zijn: we veranderen 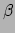 in
in 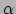 en
en
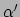 in
in
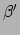 . De laatste vergelijking moet waar zijn voor elke verzameling
. De laatste vergelijking moet waar zijn voor elke verzameling
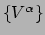 omdat
omdat  een willekeurige vector is. We vinden
een willekeurige vector is. We vinden
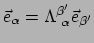 |
(113) |
en dit is de transformatiewet voor basisvectoren. Het is geen transformatie
van componenten, maar geeft de basis
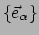 van
van
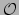 als een lineaire som van de basis
als een lineaire som van de basis
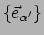 van
van
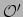 . Als we dit vergelijken met relatie (116)
dan zien we dat het transformatiegedrag verschilt. Omdat de componenten
met de inverse transformatiematrix van die van de basisvectoren transformeert,
noemen we de componenten van een vector contravariant.
. Als we dit vergelijken met relatie (116)
dan zien we dat het transformatiegedrag verschilt. Omdat de componenten
met de inverse transformatiematrix van die van de basisvectoren transformeert,
noemen we de componenten van een vector contravariant.
We kunnen de inverse transformaties vinden door ons te realiseren dat
de systemen
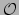 en
en
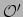 op gelijke voet
staan. We kunnen derhalve de indices met en zonder accenten verwisselen
en vinden voor de inverse transformatie van basis en componenten
op gelijke voet
staan. We kunnen derhalve de indices met en zonder accenten verwisselen
en vinden voor de inverse transformatie van basis en componenten
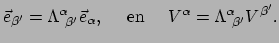 |
(114) |
Dit volgt ook uit het feit dat eerst heen en vervolgens
terug transformeren niets mag veranderen. Dit leidt tot de identiteit
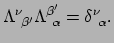 |
(115) |
Merk op dat we bovenstaand verband al hadden gevonden in vergelijking (91).
We eindigen de discussie over vectoren met een voorbeeld in
 .
Stel dat
.
Stel dat 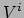 met
met 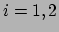 de contravariante componenten zijn van een vector,
en dat
de contravariante componenten zijn van een vector,
en dat
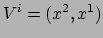 in het coördinatenstelsel
in het coördinatenstelsel
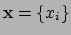 .
We willen nu de componenten van deze vector,
.
We willen nu de componenten van deze vector,
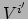 , berekenen in
het systeem
, berekenen in
het systeem
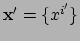 met transformatie
met transformatie
Volgens de definitie van covariantie, vergelijking (116), geldt
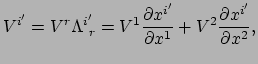 |
(117) |
waarbij we vergelijking (88) gebruikt hebben om
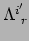 uit te werken. We zien dat we de transformatiematrix nodig hebben
voor geval
uit te werken. We zien dat we de transformatiematrix nodig hebben
voor geval  en
en  . We vinden
. We vinden
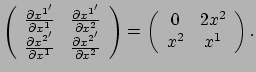 |
(118) |
Dit geeft
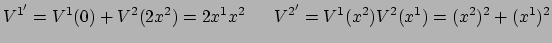 |
(119) |
en in termen van de geaccentueerde coördinaten wordt dit
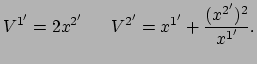 |
(120) |




Next: Lineaire functionaal, 1-vorm of
Up: Geometrische objecten
Previous: Scalairveld
Contents
Jo van den Brand
2009-01-31
![\includegraphics[width=8cm]{Figures/vectorfield.eps}](img661.png)
![\includegraphics[width=8cm]{Figures/vectorfield.eps}](img661.png)
![]() dat leeft in een bepaalde ruimte,
in ons voorbeeld van het aardoppervlak is dat een niet-euclidische twee-dimensionale ruimte met
constante positieve kromming35. De vector heeft een bepaalde betekenis
in die ruimte en stelt in ons voorbeeld de horizontale windsnelheid
op het oppervlak van de aarde voor.
We kunnen vectoren tekenen als pijltjes, zonder
te refereren naar een bepaalde basis, en dat hebben we gedaan in
Fig. 34.
dat leeft in een bepaalde ruimte,
in ons voorbeeld van het aardoppervlak is dat een niet-euclidische twee-dimensionale ruimte met
constante positieve kromming35. De vector heeft een bepaalde betekenis
in die ruimte en stelt in ons voorbeeld de horizontale windsnelheid
op het oppervlak van de aarde voor.
We kunnen vectoren tekenen als pijltjes, zonder
te refereren naar een bepaalde basis, en dat hebben we gedaan in
Fig. 34.
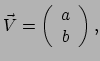
![$\displaystyle \vec V \xrightarrow[ {\mathcal{O}}^\prime ]{}
\left( \begin{array}{c}
p \\
q \\
\end{array}
\right) ,$](img670.png)
![]() de
de ![]() -component van
de
-component van
de ![]() -vector voorstelt. We bedoelen echter met
-vector voorstelt. We bedoelen echter met ![]() een volledige vector,
waarbij het subscript
een volledige vector,
waarbij het subscript ![]() onderdeel is van de naam van de vector en aangeeft
welke van de basisvectoren we bedoelen (namelijk de basisvector in de
onderdeel is van de naam van de vector en aangeeft
welke van de basisvectoren we bedoelen (namelijk de basisvector in de ![]() -richting).
De vector
-richting).
De vector ![]() heeft zelf componenten, waarvan de
heeft zelf componenten, waarvan de ![]() -component geschreven
kan worden als
-component geschreven
kan worden als
![]() . De volledige basis36
geven we in dit geval aan met {
. De volledige basis36
geven we in dit geval aan met {
![]() }.
}.
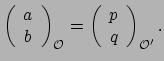
![\includegraphics[width=10cm]{Figures/tangent.eps}](img686.png)
![]() en de bijbehorende basis van eenheidsvectoren
en de bijbehorende basis van eenheidsvectoren
![]() .
We gebruiken dit systeem als algemene referentie om andere, niet cartesische
coördinaten in te beschrijven.
We hebben een tweede coördinatensysteem
.
We gebruiken dit systeem als algemene referentie om andere, niet cartesische
coördinaten in te beschrijven.
We hebben een tweede coördinatensysteem ![]() dat niet cartesisch is,
bijvoorbeeld de sferische coördinaten
dat niet cartesisch is,
bijvoorbeeld de sferische coördinaten
![]() . Er geldt
. Er geldt
![\includegraphics[width=10cm]{Figures/sferisch.eps}](img706.png)
![]() en
en
![]() snijden elkaar en dat
resulteert in de coördinaatcurve die een deellijn is die vanaf
snijden elkaar en dat
resulteert in de coördinaatcurve die een deellijn is die vanaf ![]() vertrekt
door
vertrekt
door
![]() gaat; de oppervlakken
gaat; de oppervlakken
![]() en
en ![]() snijden
elkaar in de curve die een halve cirkel is met eindpunten op de
snijden
elkaar in de curve die een halve cirkel is met eindpunten op de ![]() -as en
die door
-as en
die door
![]() gaat; en de oppervlakken
gaat; en de oppervlakken ![]() en
en
![]() snijden elkaar in de horizontale cirkel door
snijden elkaar in de horizontale cirkel door
![]() met het middelpunt
op de
met het middelpunt
op de ![]() -as.
-as.
![]() ,
krijgen we een tangentenvector aan de coördinaatcurve. Omdat we tijdens
differentiëren
,
krijgen we een tangentenvector aan de coördinaatcurve. Omdat we tijdens
differentiëren ![]() en
en ![]() constant houden (want op deze wijze was de
curve gedefinieerd), hebben we in feite de partiële afgeleide
naar
constant houden (want op deze wijze was de
curve gedefinieerd), hebben we in feite de partiële afgeleide
naar ![]() genomen van vergelijking (107). Als we op dezelfde
manier vergelijking (107) partieel afleiden naar
genomen van vergelijking (107). Als we op dezelfde
manier vergelijking (107) partieel afleiden naar ![]() en
en ![]() ,
krijgen we de tangentenvectoren van de andere twee coördinaatcurven.
De drie partiële afgeleiden
,
krijgen we de tangentenvectoren van de andere twee coördinaatcurven.
De drie partiële afgeleiden
![]() , kunnen we in elk punt
, kunnen we in elk punt
![]() de vector
de vector
![]() refereren aan basis
refereren aan basis
![]() ,
,
![]() .
Een andere notatie is
.
Een andere notatie is
![]() . Als we
willen weten wat de componenten van deze vector zijn in een ander coördinatenstelsel,
bijvoorbeeld het systeem
. Als we
willen weten wat de componenten van deze vector zijn in een ander coördinatenstelsel,
bijvoorbeeld het systeem
![]() , dan schrijven we
, dan schrijven we
![]() .
We gebruiken het accent boven de index om de nieuwe coördinaten aan te geven. De
vector
.
We gebruiken het accent boven de index om de nieuwe coördinaten aan te geven. De
vector
![]() is hetzelfde en daarvoor hebben we geen nieuwe notatie nodig
als we van referentiesysteem veranderen. We kunnen de nieuwe componenten
is hetzelfde en daarvoor hebben we geen nieuwe notatie nodig
als we van referentiesysteem veranderen. We kunnen de nieuwe componenten
![]() vinden met behulp van de transformatiematrix van
het ene naar het andere systeem (zie vergelijking (88)) en we
schrijven
vinden met behulp van de transformatiematrix van
het ene naar het andere systeem (zie vergelijking (88)) en we
schrijven
![]() ) als
) als
![]() en door de regel dat zijn componenten in een systeem
en door de regel dat zijn componenten in een systeem
![]() gegeven worden door
gegeven worden door
![]() van een vector
van een vector ![]() ten opzichte
van de natuurlijke basis
ten opzichte
van de natuurlijke basis
![]() worden de
contravariante componenten genoemd. Een object waarvan de componenten
contravariant transformeren, een vector, noemen we een
worden de
contravariante componenten genoemd. Een object waarvan de componenten
contravariant transformeren, een vector, noemen we een
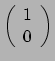 tensor.
Stel dat we twee systemen met curvelineaire coördinaten hebben
in ruimtetijd, aangegeven met
tensor.
Stel dat we twee systemen met curvelineaire coördinaten hebben
in ruimtetijd, aangegeven met
![]() en
en
![]() . We vragen ons af hoe
de contravariante componenten van een vector veranderen als we
van het ene naar het andere systeem gaan. We noemen
. We vragen ons af hoe
de contravariante componenten van een vector veranderen als we
van het ene naar het andere systeem gaan. We noemen
![]() de basis in het systeem van waarnemer
de basis in het systeem van waarnemer
![]() en
en
![]() de basis in het systeem van waarnemer
de basis in het systeem van waarnemer
![]() .
Er geldt
.
Er geldt
![]() en
en
![]() op gelijke voet
staan. We kunnen derhalve de indices met en zonder accenten verwisselen
en vinden voor de inverse transformatie van basis en componenten
op gelijke voet
staan. We kunnen derhalve de indices met en zonder accenten verwisselen
en vinden voor de inverse transformatie van basis en componenten
![]() .
Stel dat
.
Stel dat ![]() met
met ![]() de contravariante componenten zijn van een vector,
en dat
de contravariante componenten zijn van een vector,
en dat
![]() in het coördinatenstelsel
in het coördinatenstelsel
![]() .
We willen nu de componenten van deze vector,
.
We willen nu de componenten van deze vector,
![]() , berekenen in
het systeem
, berekenen in
het systeem
![]() met transformatie
met transformatie