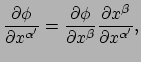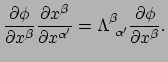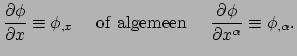Next: Algemene tensorvelden
Up: Geometrische objecten
Previous: Vectorveld
Contents
Een tensor van het type
 wordt een covector, een covariante vector, een lineaire functionaal38 of
een 1-vorm genoemd. De lineaire functionaal39
wordt een covector, een covariante vector, een lineaire functionaal38 of
een 1-vorm genoemd. De lineaire functionaal39
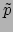 heeft een vector als argument en beeldt af op de reële getallen:
heeft een vector als argument en beeldt af op de reële getallen:
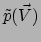 is een reëel getal40. De functionalen voldoen aan
de axioma's voor een vectorruimte. Deze ruimte wordt de duale vectorruimte
genoemd om het onderscheiden van de ruimte van alle vectoren
is een reëel getal40. De functionalen voldoen aan
de axioma's voor een vectorruimte. Deze ruimte wordt de duale vectorruimte
genoemd om het onderscheiden van de ruimte van alle vectoren  .
De componenten van
.
De componenten van 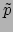 worden
worden 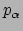 genoemd en er geldt
genoemd en er geldt
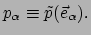 |
(121) |
Elke component met één enkel subscript is per conventie de component
van een 1-vorm; een superscript geeft een component van een vector aan.
In termen van componenten wordt
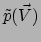 gegeven door
gegeven door
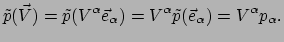 |
(122) |
Merk op dat we in bovenstaande afleiding gebruik maken van de
lineairiteit van de functionaal. Voor ruimtetijd ( ) is het getal
) is het getal
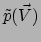 gelijk aan
gelijk aan
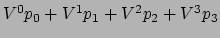 en de bewerking wordt contractie van
en de bewerking wordt contractie van  en
en 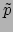 genoemd.
genoemd.
De componenten van 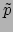 op een andere basis
op een andere basis
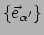 zijn
zijn
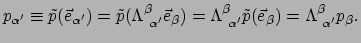 |
(123) |
Als we dit vergelijken met uitdrukking (120) dan zien we
dat de componenten van 1-vormen op precies dezelfde wijze transformeren als
basisvectoren en tegengesteld aan de componenten van vectoren. Met tegengesteld
bedoelen we met de inverse transformatie (zie weer
vergelijking (120)).
Dit gebruik van de inverse garadeert dat
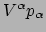 systeem
onafhankelijk is voor ieder vector
systeem
onafhankelijk is voor ieder vector  en 1-vorm
en 1-vorm 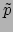 .
De inverse transformatie geeft aanleiding tot het woord duaal
in duale vectorruimte. De eigenschap van transformeren met
basisvectoren geeft aanleiding tot de co in covariante vector.
Omdat componenten van gewone vectoren tegengesteld transformeren aan
de basisvectoren, worden ze contravariant genoemd.
.
De inverse transformatie geeft aanleiding tot het woord duaal
in duale vectorruimte. De eigenschap van transformeren met
basisvectoren geeft aanleiding tot de co in covariante vector.
Omdat componenten van gewone vectoren tegengesteld transformeren aan
de basisvectoren, worden ze contravariant genoemd.
Omdat de 1-vormen een vectorruimte opbouwen, kunnen we een verzameling van
onafhankelijke 1-vormen als basis kiezen. We hebben de basis
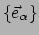 reeds gebruikt om de componenten van de 1-vorm te definiëren. We kunnen
nu de geassocieerde 1-vorm basis
reeds gebruikt om de componenten van de 1-vorm te definiëren. We kunnen
nu de geassocieerde 1-vorm basis
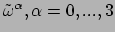 definiëren die we duaal aan
definiëren die we duaal aan
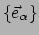 noemen. Dat wil
zeggen dat we de verzameling
noemen. Dat wil
zeggen dat we de verzameling
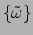 zó kiezen, dat
zó kiezen, dat
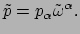 |
(124) |
We vinden op deze manier specieke 1-vormen als basis.
Merk op dat we de notatie weer zodanig kiezen, dat we gebruik kunnen
maken van de sommatieconventie. Als we vergelijking (130)
gebruiken, vinden we
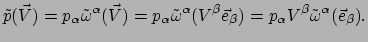 |
(125) |
Het bovenstaande dient gelijk te zijn aan
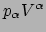 en
daaruit volgt
en
daaruit volgt
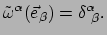 |
(126) |
Bovenstaande relatie definieert de 1-vorm basis: de vector basis
induceert een unieke en bruikbare 1-vorm basis41. We illustreren dit
aan de hand van een voorbeeld uit de 3D euclidische ruimte.
Voorbeeld: duale basis in euclidische ruimte
We beschouwen de euclidische ruimte met cartesische coördinaten 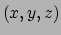 en de bijbehorende basis van eenheidsvectoren
en de bijbehorende basis van eenheidsvectoren
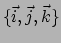 .
We gebruiken dit systeem weer als algemene referentie om een ander, niet cartesisch
systeem,
.
We gebruiken dit systeem weer als algemene referentie om een ander, niet cartesisch
systeem, 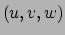 , te beschrijven.
We kunnen de gradiënt van een scalaire functie beschouwen als een
1-vorm. Teneinde dat duidelijk te maken gaan we weer even terug
naar onze beschrijving in de drie-dimensionale euclidische ruimte.
Vergelijking (112) geeft de natuurlijke
basis
, te beschrijven.
We kunnen de gradiënt van een scalaire functie beschouwen als een
1-vorm. Teneinde dat duidelijk te maken gaan we weer even terug
naar onze beschrijving in de drie-dimensionale euclidische ruimte.
Vergelijking (112) geeft de natuurlijke
basis
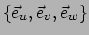 op punt
op punt
 , waarbij
we de coördinaten
, waarbij
we de coördinaten 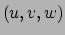 gebruiken om punten te labelen.
Er is een andere manier om het coördinatensysteem
gebruiken om punten te labelen.
Er is een andere manier om het coördinatensysteem 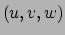 te
gebruiken om een basis te construeren op punt
te
gebruiken om een basis te construeren op punt
 .
Allereerst inverteren we vergelijkingen (107)
om
.
Allereerst inverteren we vergelijkingen (107)
om 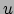 ,
, 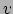 en
en 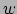 te krijgen in termen van
te krijgen in termen van 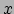 ,
, 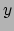 en
en 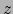 ,
,
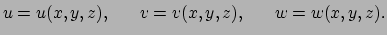 |
(127) |
Dit stelt ons in staat om elke coördinaat als een scalair veld
te beschouwen en de bijbehorende gradiënten te berekenen.
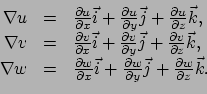 |
(128) |
Op elk punt
 staan deze gradiëntvectoren loodrecht op de
corresponderende coördinaatoppervlakken door
staan deze gradiëntvectoren loodrecht op de
corresponderende coördinaatoppervlakken door
 , die overeenkomen
met de oppervlakken
, die overeenkomen
met de oppervlakken 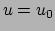 ,
, 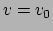 en
en 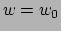 . We hebben daarom met
. We hebben daarom met
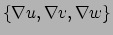 een alternatieve basis op
een alternatieve basis op
 .
Deze basis is de duale van de basis van tangentenvectoren. Teneinde
deze basis te onderscheiden van de natuurlijke basis, gebruiken we
de indices als superscipten42.
.
Deze basis is de duale van de basis van tangentenvectoren. Teneinde
deze basis te onderscheiden van de natuurlijke basis, gebruiken we
de indices als superscipten42.
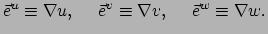 |
(129) |
Laten we nu een concreet voorbeeld beschouwen. Er geldt
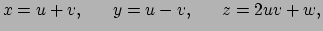 |
(130) |
waarbij
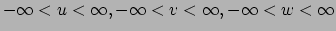 .
Inverteren van deze vergelijkingen geeft
.
Inverteren van deze vergelijkingen geeft
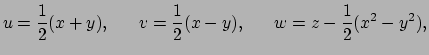 |
(131) |
waaraan we kunnen zien dat de coördinaatvlakken 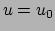 een familie
vlakken vormen, net zoals
een familie
vlakken vormen, net zoals 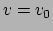 , terwijl de coördinaatvlakken
, terwijl de coördinaatvlakken 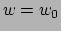 een familie hyperbolische paraboloïden vormen.
een familie hyperbolische paraboloïden vormen.
De positievector 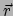 wordt gegeven door
wordt gegeven door
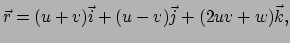 |
(132) |
waarmee we voor de vectoren van de natuurlijke basis
vinden. Enkel de laatste vector is een eenheidsvector. Geen van de inproducten
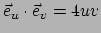 ,
,
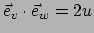 en
en
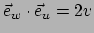 is in het algemeen gelijk aan nul. Het systeem is dus niet orthogonaal.
is in het algemeen gelijk aan nul. Het systeem is dus niet orthogonaal.
We vinden voor de vectoren van de duale basis
We zien dat in het algemeen 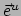 niet parallel is met
niet parallel is met 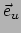 ,
,
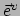 niet met
niet met 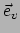 , en
, en 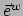 niet met
niet met 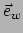 .
.
Gegeven een vectorveld
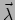 kunnen we op elk punt
kunnen we op elk punt
 de
vector
de
vector
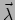 beschrijven ten opzichte van de natuurlijke basis
beschrijven ten opzichte van de natuurlijke basis
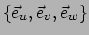 of de duale basis
of de duale basis
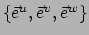 .
We schrijven
.
We schrijven
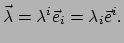 |
(135) |
Figuur:
Links: de waarde
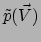 is gelijk aan 2,5.
Rechts: een topologische kaart demonstreert de gradiënt 1-vorm (lokale
contouren van constante hoogte). De verandering van hoogte voor een
reis (pijl) is het aantal contouren dat door de pijl doorboort wordt.
Deze is het grootst voor reis (2).
is gelijk aan 2,5.
Rechts: een topologische kaart demonstreert de gradiënt 1-vorm (lokale
contouren van constante hoogte). De verandering van hoogte voor een
reis (pijl) is het aantal contouren dat door de pijl doorboort wordt.
Deze is het grootst voor reis (2).
|
|
Bij vectoren denken we meestal aan een pijl als we een beeld nodig hebben.
Het kan handig zijn om ook een voorstelling van een 1-vorm te hebben.
Dit beeld moet het feit uitdrukken dat een 1-vorm een afbeelding
is van een vector naar een reëel getal. In de drie-dimensionale
ruimte kan men zich een 1-vorm 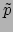 op punt
op punt
 voorstellen als een aantal parallelle vlakken. De contractie met een
vector
voorstellen als een aantal parallelle vlakken. De contractie met een
vector  is dan het aantal vlakken dat door de vector
`doorboort' wordt. Hoe dichter de oppervlakken bij elkaar staan,
hoe groter
is dan het aantal vlakken dat door de vector
`doorboort' wordt. Hoe dichter de oppervlakken bij elkaar staan,
hoe groter
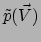 .
.
Het dualisme is overigens compleet, omdat we vectoren ook kunnen beschouwen als
functies die 1-vormen afbeelden op de reële getallen. Gegeven vector  krijgen we een reëel getal als we de vector voorzien van een 1-vorm,
krijgen we een reëel getal als we de vector voorzien van een 1-vorm,
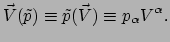 |
(136) |
Vectoren hebben dus geen speciale positie als objecten die als input
dienen voor tensoren. We kunnen een vector ook als tensor zien: een lineaire
functie van een 1-vorm naar een reëel getal. Vectoren en 1-vormen hebben
hiermee een gelijke en symmetrische status.
Voordat we de beschrijving van 1-vormen afsluiten zullen we nog een
speciale 1-vorm bespreken, de gradiënt. Beschouw een scalairveld
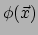 . De wereldlijn van een waarnemer meet een waarde voor
. De wereldlijn van een waarnemer meet een waarde voor 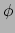 voor elke gebeurtenis die hij meemaakt en deze waarde verandert voortdurend.
We parametriseren de wereldlijn met de eigentijd
voor elke gebeurtenis die hij meemaakt en deze waarde verandert voortdurend.
We parametriseren de wereldlijn met de eigentijd 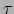 van de waarnemer
en dit staat ons toe om de coördinaten van gebeurtenissen op de wereldlijn
uit te drukken als functies van
van de waarnemer
en dit staat ons toe om de coördinaten van gebeurtenissen op de wereldlijn
uit te drukken als functies van 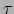 . Er geldt
. Er geldt
![$ [ t=t(\tau ), x=x( \tau ), y=y( \tau ), z=z(\tau )]$](img811.png) . De viersnelheid
heeft componenten
. De viersnelheid
heeft componenten
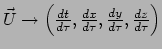 en omdat
en omdat 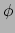 een functie is van
een functie is van 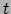 ,
, 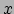 ,
, 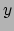 en
en 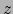 , is
, is 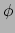 op de
wereldlijn impliciet een functie van
op de
wereldlijn impliciet een functie van 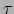 ,
,
![$ \phi(\tau ) = \phi[t(\tau ), x( \tau ), y( \tau ), z(\tau )]$](img813.png) .
De mate van verandering van
.
De mate van verandering van 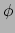 op de wereldlijn, dat is de
afgeleide, bedraagt
op de wereldlijn, dat is de
afgeleide, bedraagt
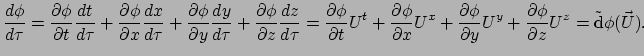 |
(137) |
Het is duidelijk dat we in bovenstaande vergelijking erin geslaagd zijn
om met de vector 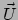 het getal
het getal
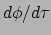 te produceren, dat
de mate van verandering van
te produceren, dat
de mate van verandering van 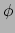 is langs de wereldlijn waaraan
is langs de wereldlijn waaraan
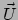 een tangent vector is. Dit getal
een tangent vector is. Dit getal
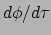 is duidelijk
een lineaire functie van
is duidelijk
een lineaire functie van 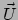 en hiermee hebben we dus een 1-vorm
gedefinieerd. Vergelijken met uitdrukking (128) toont
dat deze 1-vorm de componenten
en hiermee hebben we dus een 1-vorm
gedefinieerd. Vergelijken met uitdrukking (128) toont
dat deze 1-vorm de componenten
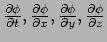 heeft.
Deze 1-vorm wordt de gradiënt van
heeft.
Deze 1-vorm wordt de gradiënt van 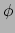 genoemd en aangeduid met
genoemd en aangeduid met
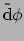 .
Er geldt
.
Er geldt
![$\displaystyle \tilde {\rm d}\phi \xrightarrow[{\mathcal{O}}]{} \left(
{\partia...
...phi~~{\rm met~} \nabla_\alpha \phi =
{\partial \phi \over \partial x^\alpha} .$](img819.png) |
(138) |
Merk op dat ondanks de notatie,
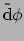 niet klein hoeft te zijn.
We dus verder dat de gradiënt een 1-vorm is, terwijl we in de vectoranalyse
geleerd hebben dat het een vectorgrootheid is. De reden hiervoor is dat
er een metriek nodig is om 1-vormen aan vectoren te relateren. Op dit
moment hebben we deze extra mathematische structuur nog niet aan onze
variëteit opgelegd.
niet klein hoeft te zijn.
We dus verder dat de gradiënt een 1-vorm is, terwijl we in de vectoranalyse
geleerd hebben dat het een vectorgrootheid is. De reden hiervoor is dat
er een metriek nodig is om 1-vormen aan vectoren te relateren. Op dit
moment hebben we deze extra mathematische structuur nog niet aan onze
variëteit opgelegd.
We kunnen vergelijking (144) nog controleren op haar consistentie
door te bestuderen hoe de componenten transformeren. Voor een 1-vorm
moet gelden
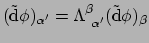 .
We weten hoe partiële afgeleiden transformeren, namelijk
.
We weten hoe partiële afgeleiden transformeren, namelijk
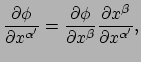 |
(139) |
hetgeen betekent dat
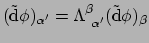 , want
gegeven dat
, want
gegeven dat
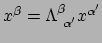 geldt
geldt
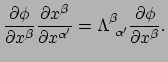 |
(140) |
De componenten van de gradiënt transformeren met de inverse van de
componenten van vectoren. De gradiënt is dus een 1-vorm.
Van nu af aan zullen we partiële afgeleiden aanduiden met de komma-notatie.
Er geldt de definitie
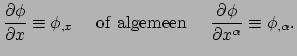 |
(141) |
Merk op dat de index 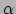 aan de linkerkant als een boven-index
optreedt en aan de rechterkant als een beneden-index.
aan de linkerkant als een boven-index
optreedt en aan de rechterkant als een beneden-index.




Next: Algemene tensorvelden
Up: Geometrische objecten
Previous: Vectorveld
Contents
Jo van den Brand
2009-01-31
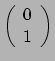 wordt een covector, een covariante vector, een lineaire functionaal38 of
een 1-vorm genoemd. De lineaire functionaal39
wordt een covector, een covariante vector, een lineaire functionaal38 of
een 1-vorm genoemd. De lineaire functionaal39
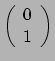 wordt een covector, een covariante vector, een lineaire functionaal38 of
een 1-vorm genoemd. De lineaire functionaal39
wordt een covector, een covariante vector, een lineaire functionaal38 of
een 1-vorm genoemd. De lineaire functionaal39
![]() heeft een vector als argument en beeldt af op de reële getallen:
heeft een vector als argument en beeldt af op de reële getallen:
![]() is een reëel getal40. De functionalen voldoen aan
de axioma's voor een vectorruimte. Deze ruimte wordt de duale vectorruimte
genoemd om het onderscheiden van de ruimte van alle vectoren
is een reëel getal40. De functionalen voldoen aan
de axioma's voor een vectorruimte. Deze ruimte wordt de duale vectorruimte
genoemd om het onderscheiden van de ruimte van alle vectoren ![]() .
De componenten van
.
De componenten van ![]() worden
worden ![]() genoemd en er geldt
genoemd en er geldt
![]() op een andere basis
op een andere basis
![]() zijn
zijn
![]() reeds gebruikt om de componenten van de 1-vorm te definiëren. We kunnen
nu de geassocieerde 1-vorm basis
reeds gebruikt om de componenten van de 1-vorm te definiëren. We kunnen
nu de geassocieerde 1-vorm basis
![]() definiëren die we duaal aan
definiëren die we duaal aan
![]() noemen. Dat wil
zeggen dat we de verzameling
noemen. Dat wil
zeggen dat we de verzameling
![]() zó kiezen, dat
zó kiezen, dat
![]() en de bijbehorende basis van eenheidsvectoren
en de bijbehorende basis van eenheidsvectoren
![]() .
We gebruiken dit systeem weer als algemene referentie om een ander, niet cartesisch
systeem,
.
We gebruiken dit systeem weer als algemene referentie om een ander, niet cartesisch
systeem, ![]() , te beschrijven.
We kunnen de gradiënt van een scalaire functie beschouwen als een
1-vorm. Teneinde dat duidelijk te maken gaan we weer even terug
naar onze beschrijving in de drie-dimensionale euclidische ruimte.
Vergelijking (112) geeft de natuurlijke
basis
, te beschrijven.
We kunnen de gradiënt van een scalaire functie beschouwen als een
1-vorm. Teneinde dat duidelijk te maken gaan we weer even terug
naar onze beschrijving in de drie-dimensionale euclidische ruimte.
Vergelijking (112) geeft de natuurlijke
basis
![]() op punt
op punt
![]() , waarbij
we de coördinaten
, waarbij
we de coördinaten ![]() gebruiken om punten te labelen.
Er is een andere manier om het coördinatensysteem
gebruiken om punten te labelen.
Er is een andere manier om het coördinatensysteem ![]() te
gebruiken om een basis te construeren op punt
te
gebruiken om een basis te construeren op punt
![]() .
Allereerst inverteren we vergelijkingen (107)
om
.
Allereerst inverteren we vergelijkingen (107)
om ![]() ,
, ![]() en
en ![]() te krijgen in termen van
te krijgen in termen van ![]() ,
, ![]() en
en ![]() ,
,
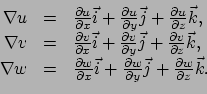
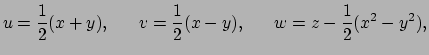
![]() wordt gegeven door
wordt gegeven door
![]() kunnen we op elk punt
kunnen we op elk punt
![]() de
vector
de
vector
![]() beschrijven ten opzichte van de natuurlijke basis
beschrijven ten opzichte van de natuurlijke basis
![]() of de duale basis
of de duale basis
![]() .
We schrijven
.
We schrijven
![\includegraphics[width=12cm]{Figures/1vorm.eps}](img807.png)
![]() op punt
op punt
![]() voorstellen als een aantal parallelle vlakken. De contractie met een
vector
voorstellen als een aantal parallelle vlakken. De contractie met een
vector ![]() is dan het aantal vlakken dat door de vector
`doorboort' wordt. Hoe dichter de oppervlakken bij elkaar staan,
hoe groter
is dan het aantal vlakken dat door de vector
`doorboort' wordt. Hoe dichter de oppervlakken bij elkaar staan,
hoe groter
![]() .
.
![]() krijgen we een reëel getal als we de vector voorzien van een 1-vorm,
krijgen we een reëel getal als we de vector voorzien van een 1-vorm,
![]() . De wereldlijn van een waarnemer meet een waarde voor
. De wereldlijn van een waarnemer meet een waarde voor ![]() voor elke gebeurtenis die hij meemaakt en deze waarde verandert voortdurend.
We parametriseren de wereldlijn met de eigentijd
voor elke gebeurtenis die hij meemaakt en deze waarde verandert voortdurend.
We parametriseren de wereldlijn met de eigentijd ![]() van de waarnemer
en dit staat ons toe om de coördinaten van gebeurtenissen op de wereldlijn
uit te drukken als functies van
van de waarnemer
en dit staat ons toe om de coördinaten van gebeurtenissen op de wereldlijn
uit te drukken als functies van ![]() . Er geldt
. Er geldt
![]() . De viersnelheid
heeft componenten
. De viersnelheid
heeft componenten
![]() en omdat
en omdat ![]() een functie is van
een functie is van ![]() ,
, ![]() ,
, ![]() en
en ![]() , is
, is ![]() op de
wereldlijn impliciet een functie van
op de
wereldlijn impliciet een functie van ![]() ,
,
![]() .
De mate van verandering van
.
De mate van verandering van ![]() op de wereldlijn, dat is de
afgeleide, bedraagt
op de wereldlijn, dat is de
afgeleide, bedraagt
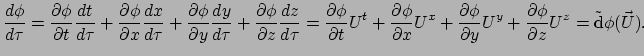
![]() .
We weten hoe partiële afgeleiden transformeren, namelijk
.
We weten hoe partiële afgeleiden transformeren, namelijk