



Next: Metrische tensor
Up: Geometrische objecten
Previous: Lineaire functionaal, 1-vorm of
Contents
De
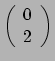 tensoren
zijn tensoren die twee vectorargumenten hebben. Een voorbeeld is de
metrische tensor, maar een eenvoudiger voorbeeld is het product van
twee 1-vormen. We gebruiken hierbij de volgende regel: als
tensoren
zijn tensoren die twee vectorargumenten hebben. Een voorbeeld is de
metrische tensor, maar een eenvoudiger voorbeeld is het product van
twee 1-vormen. We gebruiken hierbij de volgende regel: als 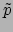 en
en 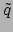 beide 1-vormen zijn, dan is
beide 1-vormen zijn, dan is
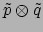 de
de
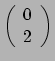 tensor die, als
hij de vectoren
tensor die, als
hij de vectoren 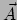 en
en 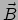 als argumenten krijgt, het getal
als argumenten krijgt, het getal
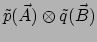 produceert. Het is dus
het product van de getallen geproduceert door de
produceert. Het is dus
het product van de getallen geproduceert door de
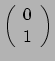 tensoren.
Het symbool
tensoren.
Het symbool  wordt het tensorproduct genoemd en geeft de formele
notatie hoe we een
wordt het tensorproduct genoemd en geeft de formele
notatie hoe we een
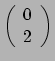 tensor moeten samenstellen uit 1-vormen. Overigens is
tensor moeten samenstellen uit 1-vormen. Overigens is  niet
commutatief:
niet
commutatief:
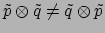 zijn verschillende tensoren. De eerste geeft de waarde
zijn verschillende tensoren. De eerste geeft de waarde
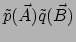 en de tweede
en de tweede
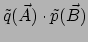 .
.
De meest algemene
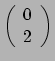 tensor geen eenvoudig tensorproduct van twee 1-vormen, maar kan wel
altijd voorgesteld worden als een som van dergelijke tensoren. Hiertoe
beschouwen we de componenten van een willekeurige
tensor geen eenvoudig tensorproduct van twee 1-vormen, maar kan wel
altijd voorgesteld worden als een som van dergelijke tensoren. Hiertoe
beschouwen we de componenten van een willekeurige
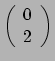 tensor
tensor 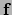 .
Er geldt
.
Er geldt
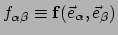 ,
waarbij elke index vier waarden kan aannemen voor ruimtetijd. In totaal
heeft
,
waarbij elke index vier waarden kan aannemen voor ruimtetijd. In totaal
heeft 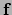 dus 16 componenten. De waarde van
dus 16 componenten. De waarde van 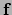 voor
willekeurige vectoren is
voor
willekeurige vectoren is
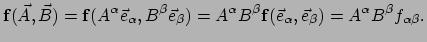 |
(142) |
De vraag is of we een basis kunnen vormen voor deze tensoren43. Kunnen we
een verzameling bestaande uit 16 verschillende
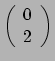 tensoren
tensoren
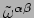 definiëren, zodat geldt
definiëren, zodat geldt
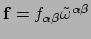 ? Als dat zo is,
dan dient te gelden
? Als dat zo is,
dan dient te gelden
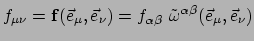 |
(143) |
en dat betekent, dat moet gelden
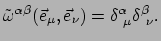 |
(144) |
Volgens vergelijking (132) is
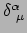 de
waarde van
de
waarde van
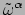 voor
voor
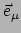 en hetzelfde verhaal
voor
en hetzelfde verhaal
voor
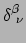 . Daarom is
. Daarom is
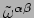 een
tensor, waarvan de waarde het product is van de waarden van de twee
basis 1-vormen. We concluderen derhalve
een
tensor, waarvan de waarde het product is van de waarden van de twee
basis 1-vormen. We concluderen derhalve
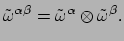 |
(145) |
De tensoren
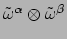 vormen een basis
voor alle
vormen een basis
voor alle
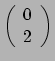 tensoren, en we mogen schrijven
tensoren, en we mogen schrijven
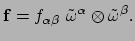 |
(146) |
Op deze wijze is een algemene
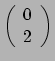 tensor een som over eenvoudige tensorproduct tensoren.
tensor een som over eenvoudige tensorproduct tensoren.
Een tensor van het type
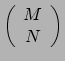 is een afbeelding (functie) van
is een afbeelding (functie) van 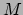 1-vormen en
1-vormen en 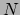 vectoren naar reële getallen,
die lineair is in elk van zijn
vectoren naar reële getallen,
die lineair is in elk van zijn 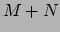 argumenten44.
Merk op dat deze definitie van een
tensor niet spreekt over de componenten van de 1-vormen en vectoren. De tensor
dient hetzelfde reële getal als uitkomst te geven, onafhankelijk
van het gebruikte coördinatensysteem.
argumenten44.
Merk op dat deze definitie van een
tensor niet spreekt over de componenten van de 1-vormen en vectoren. De tensor
dient hetzelfde reële getal als uitkomst te geven, onafhankelijk
van het gebruikte coördinatensysteem.
Net als een 1-vorm en vector heeft ook een tensor componenten. De definitie is
als volgt: de componenten in een referentiesysteem
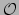 van
een tensor van het type
van
een tensor van het type
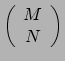 zijn de waarden van de functie als men voor de argumenten de
basis 1-vormen
zijn de waarden van de functie als men voor de argumenten de
basis 1-vormen
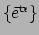 en basisvectoren
en basisvectoren
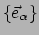 van het systeem
van het systeem
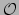 gebruikt.
De componenten van een tensor zijn dus afhankelijk van het referentiesysteem
van de waarnemer, omdat de basis immers per systeem verschilt. De tensor zelf
kan gezien worden als een topologisch object dat zelfstandig bestaat in
ruimtetijd en onafhankelijk gezien kan worden van coördinatenstelsels.
gebruikt.
De componenten van een tensor zijn dus afhankelijk van het referentiesysteem
van de waarnemer, omdat de basis immers per systeem verschilt. De tensor zelf
kan gezien worden als een topologisch object dat zelfstandig bestaat in
ruimtetijd en onafhankelijk gezien kan worden van coördinatenstelsels.




Next: Metrische tensor
Up: Geometrische objecten
Previous: Lineaire functionaal, 1-vorm of
Contents
Jo van den Brand
2009-01-31
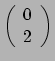 tensoren
zijn tensoren die twee vectorargumenten hebben. Een voorbeeld is de
metrische tensor, maar een eenvoudiger voorbeeld is het product van
twee 1-vormen. We gebruiken hierbij de volgende regel: als
tensoren
zijn tensoren die twee vectorargumenten hebben. Een voorbeeld is de
metrische tensor, maar een eenvoudiger voorbeeld is het product van
twee 1-vormen. We gebruiken hierbij de volgende regel: als 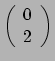 tensor die, als
hij de vectoren
tensor die, als
hij de vectoren 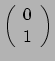 tensoren.
Het symbool
tensoren.
Het symbool 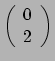 tensor moeten samenstellen uit 1-vormen. Overigens is
tensor moeten samenstellen uit 1-vormen. Overigens is 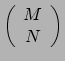 is een afbeelding (functie) van
is een afbeelding (functie) van