



Next: De speciale relativiteitstheorie
Up: Wiskunde I - Differentiaaltopologie
Previous: Algemene tensorvelden
Contents
Tot nu toe hebben we enkel variëteiten beschouwd die een
relatief eenvoudige vorm hebben.
De variëteit is continu en differentieerbaar, waardoor we 1-vormen, vectoren
en andere tensoren kunnen definiëren. Verder betreft het een
amorfe verzameling punten (of puntgebeurtenissen). Er is nog geen
meetkunde gedefinieerd. Zo kunnen we twee vectoren (of 1-vormen) niet
afbeelden op een reëel getal. Er is dan ook nog geen concept van inproduct.
Als volgende stap kiezen we nu een
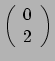 tensor die dienst gaat doen als de metriek van de variëteit. Een dergelijke
variëteit noemen we een riemannse variëteit. De metrische tensor
maakt het mogelijk om de (kwadratische) lengte van een vector
te berekenen, of het scalaire product (inproduct) van twee
vectoren te bepalen. Ook levert de metriek een één op één
correspondentie tussen vectoren en 1-vormen. We definiëren
tensor die dienst gaat doen als de metriek van de variëteit. Een dergelijke
variëteit noemen we een riemannse variëteit. De metrische tensor
maakt het mogelijk om de (kwadratische) lengte van een vector
te berekenen, of het scalaire product (inproduct) van twee
vectoren te bepalen. Ook levert de metriek een één op één
correspondentie tussen vectoren en 1-vormen. We definiëren
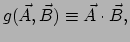 |
(147) |
en hieruit volgt direct dat de metrische tensor symmetrisch is,
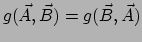 .
We beschouwen
.
We beschouwen  als een functie met twee argumenten en die lineair
is in deze argumenten, bijvoorbeeld
als een functie met twee argumenten en die lineair
is in deze argumenten, bijvoorbeeld
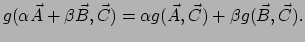 |
(148) |
Merk op dat deze definitie van metriek geen gebruik maakt van de componenten
van de vectoren. De metriek kan weer gezien worden als een topologisch
object in ruimtetijd. In een specifieke basis
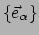 heeft de metrische tensor componenten die gegeven zijn door
heeft de metrische tensor componenten die gegeven zijn door
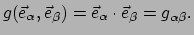 |
(149) |
De fundamentele rol van de metriek is om te zorgen voor een afbeelding
tussen vectoren en 1-vormen. Om te begrijpen hoe dit werkt, beschouwen
we 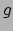 en een enkele vector
en een enkele vector  . Omdat
. Omdat 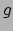 twee vector argumenten
nodig heeft, kunnen we de uitdrukking
twee vector argumenten
nodig heeft, kunnen we de uitdrukking
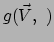 , waar nog een
argument ontbreekt, beschouwen als een functie van vectoren. Als men
aan
, waar nog een
argument ontbreekt, beschouwen als een functie van vectoren. Als men
aan
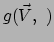 nog een vector toekent, dan krijgen we een reëel
getal. Een dergelijke lineaire functie van vectoren die een reëel
getal produceert, noemen we een 1-vorm. We noemen het
nog een vector toekent, dan krijgen we een reëel
getal. Een dergelijke lineaire functie van vectoren die een reëel
getal produceert, noemen we een 1-vorm. We noemen het 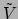 .
Er geldt
.
Er geldt
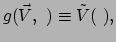 |
(150) |
waar we tussen de haakjes het vector argument moeten aanleveren.
Dan geldt dat 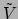 de 1-vorm is, die voor de vector
de 1-vorm is, die voor de vector 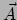 de waarde
de waarde
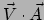 heeft. Er geldt
heeft. Er geldt
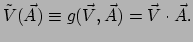 |
(151) |
Omdat 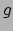 symmetrisch is, kunnen we ook schrijven
symmetrisch is, kunnen we ook schrijven
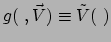 .
De componenten van
.
De componenten van 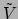 vinden we als volgt,
vinden we als volgt,
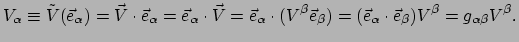 |
(152) |
Hiermee hebben we de relatie tussen vectoren en 1-vormen gevonden,
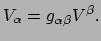 |
(153) |
We onderscheiden de componenten 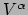 van de vector
van de vector  van de componenten
van de componenten 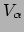 van de 1-vorm
van de 1-vorm 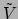 enkel
door de positie van de index
enkel
door de positie van de index 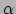 . De inverse van de metriek
bestaat ook en wordt aangeduid met
. De inverse van de metriek
bestaat ook en wordt aangeduid met
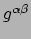 . Hiermee
vinden we
. Hiermee
vinden we
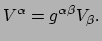 |
(154) |
Een vector is een
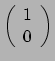 tensor en een 1-vorm is een
tensor en een 1-vorm is een
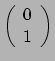 tensor. We gebruiken de metrische tensor als afbeelding tussen beide.
Op dezelfde manier kunnen we een
tensor. We gebruiken de metrische tensor als afbeelding tussen beide.
Op dezelfde manier kunnen we een
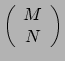 tensor afbeelden op een
tensor afbeelden op een
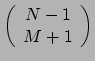 tensor, of door gebruik te maken van de inverse metriek op een
tensor, of door gebruik te maken van de inverse metriek op een
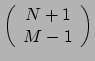 tensor. Het is gebruikelijk om voor deze geassocieerde tensoren hetzelfde
symbool te gebruiken, maar we dienen ons ervan bewust te zijn
dat we te maken hebben met verschillende tensoren. Stel
tensor. Het is gebruikelijk om voor deze geassocieerde tensoren hetzelfde
symbool te gebruiken, maar we dienen ons ervan bewust te zijn
dat we te maken hebben met verschillende tensoren. Stel
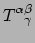 zijn de componenten van een
zijn de componenten van een
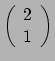 tensor. Dan zijn
tensor. Dan zijn
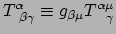 |
(155) |
de componenten van een
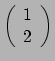 tensor, omdat
we het tweede 1-vorm argument veranderd hebben in een vector.
We noemen dergelijke manipulaties het naar boven brengen en naar
beneden halen van indices en gebruiken hierbij de metriek als afbeelding.
tensor, omdat
we het tweede 1-vorm argument veranderd hebben in een vector.
We noemen dergelijke manipulaties het naar boven brengen en naar
beneden halen van indices en gebruiken hierbij de metriek als afbeelding.
We kunnen dit ook doen met de metriek zelf en vinden
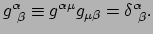 |
(156) |
De laatste stap volgt uit het feit dat
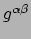 en
en
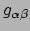 elkaars inverse afbeelding zijn.
elkaars inverse afbeelding zijn.
Een differentieerbare variëteit is een riemannse variëteit als de
kwadratische booglengte langs een curve voldoet aan
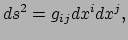 |
(157) |
waarbij de componenten van de metrische tensor,
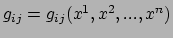 ,
continue functies zijn van de coördinaten en verschillen van constanten.
In het speciale geval dat
,
continue functies zijn van de coördinaten en verschillen van constanten.
In het speciale geval dat
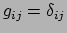 , reduceert de riemannse ruimte
tot de euclidische ruimte
, reduceert de riemannse ruimte
tot de euclidische ruimte
 . De ruimte is vlak als het mogelijk
is om een coördinatentransformatie te vinden, waarvoor
. De ruimte is vlak als het mogelijk
is om een coördinatentransformatie te vinden, waarvoor
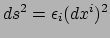 ,
waarbij iedere
,
waarbij iedere
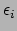 gelijk is aan
gelijk is aan 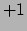 of
of 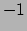 . Een ruimte die niet
vlak is, wordt gekromd genoemd.
. Een ruimte die niet
vlak is, wordt gekromd genoemd.
De ruimtetijd van Minkowski is een van de belangrijkste differentieerbare variëteiten,
het is de ruimtetijd die beschreven wordt door de speciale relativiteitstheorie.
Eenvoudige behandelingen van SRT introduceren de bijbehorende minkowskimetriek zelfs
niet expliciet, maar geven ons wel alle ingrediënten die we nodig hebben
om deze af te leiden. In het bijzonder weten we dat er voorkeurstelsel zijn
voor de coördinaten, de zogenaamde Lorentzframes, en dat als twee gebeurtenissen
gescheiden zijn door coördinaatafstanden
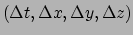 in een dergelijk frame, dan is het getal
in een dergelijk frame, dan is het getal
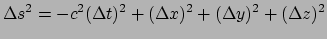 |
(158) |
onafhankelijk van het Lorentzframe. Als we onze coördinaten herdefiniëren
door
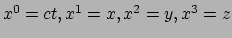 en griekse letters gebruiken als ruimtetijd
indices, dan vinden we
en griekse letters gebruiken als ruimtetijd
indices, dan vinden we
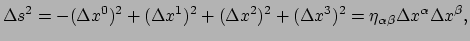 |
(159) |
waarbij
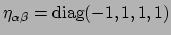 . We zien dat
. We zien dat
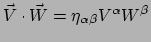 en
en
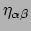 is in feite de metrische tensor en het Lorentzframe vormt de geassocieerde
orthonormale basis. We zien direct de associatie tussen de componenten van
een vector en zijn geassocieerde 1-vorm. In een Lorentzframe geldt
is in feite de metrische tensor en het Lorentzframe vormt de geassocieerde
orthonormale basis. We zien direct de associatie tussen de componenten van
een vector en zijn geassocieerde 1-vorm. In een Lorentzframe geldt
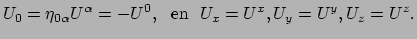 |
(160) |
Een variëteit met metriek 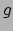 wordt enkel een minkowski ruimtetijd genoemd
als er één enkel coördinatenstelsel bestaat dat de gehele variëteit bedekt
en waarin
wordt enkel een minkowski ruimtetijd genoemd
als er één enkel coördinatenstelsel bestaat dat de gehele variëteit bedekt
en waarin 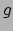 de componenten
de componenten
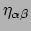 heeft.
heeft.




Next: De speciale relativiteitstheorie
Up: Wiskunde I - Differentiaaltopologie
Previous: Algemene tensorvelden
Contents
Jo van den Brand
2009-01-31
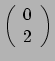 tensor die dienst gaat doen als de metriek van de variëteit. Een dergelijke
variëteit noemen we een riemannse variëteit. De metrische tensor
maakt het mogelijk om de (kwadratische) lengte van een vector
te berekenen, of het scalaire product (inproduct) van twee
vectoren te bepalen. Ook levert de metriek een één op één
correspondentie tussen vectoren en 1-vormen. We definiëren
tensor die dienst gaat doen als de metriek van de variëteit. Een dergelijke
variëteit noemen we een riemannse variëteit. De metrische tensor
maakt het mogelijk om de (kwadratische) lengte van een vector
te berekenen, of het scalaire product (inproduct) van twee
vectoren te bepalen. Ook levert de metriek een één op één
correspondentie tussen vectoren en 1-vormen. We definiëren
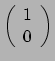 tensor en een 1-vorm is een
tensor en een 1-vorm is een
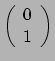 tensor. We gebruiken de metrische tensor als afbeelding tussen beide.
Op dezelfde manier kunnen we een
tensor. We gebruiken de metrische tensor als afbeelding tussen beide.
Op dezelfde manier kunnen we een
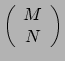 tensor afbeelden op een
tensor afbeelden op een
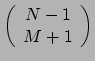 tensor, of door gebruik te maken van de inverse metriek op een
tensor, of door gebruik te maken van de inverse metriek op een
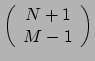 tensor. Het is gebruikelijk om voor deze geassocieerde tensoren hetzelfde
symbool te gebruiken, maar we dienen ons ervan bewust te zijn
dat we te maken hebben met verschillende tensoren. Stel
tensor. Het is gebruikelijk om voor deze geassocieerde tensoren hetzelfde
symbool te gebruiken, maar we dienen ons ervan bewust te zijn
dat we te maken hebben met verschillende tensoren. Stel
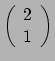 tensor. Dan zijn
tensor. Dan zijn
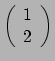 tensor, omdat
we het tweede 1-vorm argument veranderd hebben in een vector.
We noemen dergelijke manipulaties het naar boven brengen en naar
beneden halen van indices en gebruiken hierbij de metriek als afbeelding.
tensor, omdat
we het tweede 1-vorm argument veranderd hebben in een vector.
We noemen dergelijke manipulaties het naar boven brengen en naar
beneden halen van indices en gebruiken hierbij de metriek als afbeelding.