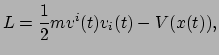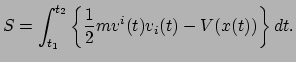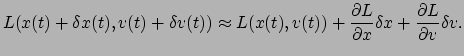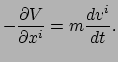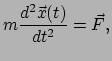Next: Het principe van Mach
Up: Klassieke mechanica
Previous: Gravitatie en getijdenkrachten
Contents
Newtoniaanse mechanica en het formalisme van Lagrange
De bewegingswetten van Newton zijn algemeen bekend. De bekendste is waarschijnlijk
dat deeltjes zich in een rechte lijn en met constante snelheid voortbewegen zolang
er geen krachten op werken. Dit wordt mathematisch uitgedrukt als
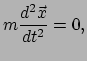 |
(23) |
waar
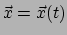 de positie van het deeltje is, en
de positie van het deeltje is, en 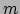 zijn massa.
Indien er een kracht
zijn massa.
Indien er een kracht 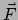 op het deeltje werkt, komt deze aan de rechterzijde
van deze vergelijking te staan. Deze formule is de basis van de Newtoniaanse
mechanica en levert een stappenplan voor het oplossen van mechanische vraagstukken:
vul de kracht in die op een deeltje werkt, los de resulterende vergelijking op,
en de positie van het deeltje als functie van de tijd is dan bekend.
op het deeltje werkt, komt deze aan de rechterzijde
van deze vergelijking te staan. Deze formule is de basis van de Newtoniaanse
mechanica en levert een stappenplan voor het oplossen van mechanische vraagstukken:
vul de kracht in die op een deeltje werkt, los de resulterende vergelijking op,
en de positie van het deeltje als functie van de tijd is dan bekend.
De tweede wet kan niet worden afgeleid; het is een experimenteel gegeven. Als wij
deze willen uitbreiden naar een versie die geldt in de speciale relativiteitstheorie,
is er net zo min een concrete afleiding beschikbaar. Wel kan er een uitbreiding
geloofwaardig worden gemaakt door gebruik te maken van de
minkowksimetriek en het relativiteitsprincipe. Het is dan vervolgens aan
experiment om aan te tonen of de gevonden uitbreiding van Newtons tweede wet geldt of
niet. Dit blijkt het geval te zijn en we geven deze afleiding
in sectie 5.11. Hier geven we een soortgelijke afleiding
voor de tweede wet van Newton. We zullen in sectie 5.11
zien dat de relativistische uitbreiding nog maar een kleine stap is. Het
formalisme dat we hiervoor zullen gebruiken is dat van Lagrange.
Lagrange (1736-1813) ontwikkelde een nieuwe manier van mechanica doen,
gebaseerd op een functie die nu zijn naam draagt: de Lagrangiaan 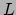 .
Deze functie is gedefinieerd als het verschil tussen de kinetische energie
.
Deze functie is gedefinieerd als het verschil tussen de kinetische energie 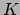 van een deeltje, en zijn potentiële energie
van een deeltje, en zijn potentiële energie 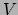
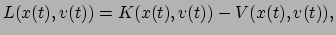 |
(24) |
en deze functie geïntegreerd over de tijdsduur van een fysisch proces noemt
met de actie 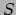 ,
,
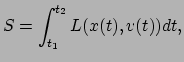 |
(25) |
waarin 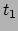 het tijdstip van begin van het proces is, en
het tijdstip van begin van het proces is, en 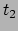 het tijdstip
van het eind van het proces. Zoals al gesuggereerd door onze notatie, heeft
de Lagrangiaan van een deeltje in het algemeen geen constante waarde. Dit
komt doordat de kinetische energie en de potentiële energie in het algemeen
geen constante waarden hebben, omdat zij functies zijn van de positie en
snelheid van het deeltje. Beschouw als voorbeeld een deeltje in het
zwaartekrachtsveld van de aarde: de potentiële energie is laag wanneer dit
deeltje dicht bij de aarde is, maar hoog wanneer het ver weg is; de kinetische
energie neemt echter toe wannneer het deeltje onder invloed van die
zwaartekracht steeds sneller naar de aarde valt. Dit voorbeeld laat zien dat
de waarde van de Lagrangiaan van een deeltje in het algemeen afhankelijk is
van de positie en snelheid van het deeltje. Deze zijn op hun beurt weer
functies van de tijd, dus uiteindelijk is de Lagrangiaan een geheel
tijdsafhankelijke functie. De actie
het tijdstip
van het eind van het proces. Zoals al gesuggereerd door onze notatie, heeft
de Lagrangiaan van een deeltje in het algemeen geen constante waarde. Dit
komt doordat de kinetische energie en de potentiële energie in het algemeen
geen constante waarden hebben, omdat zij functies zijn van de positie en
snelheid van het deeltje. Beschouw als voorbeeld een deeltje in het
zwaartekrachtsveld van de aarde: de potentiële energie is laag wanneer dit
deeltje dicht bij de aarde is, maar hoog wanneer het ver weg is; de kinetische
energie neemt echter toe wannneer het deeltje onder invloed van die
zwaartekracht steeds sneller naar de aarde valt. Dit voorbeeld laat zien dat
de waarde van de Lagrangiaan van een deeltje in het algemeen afhankelijk is
van de positie en snelheid van het deeltje. Deze zijn op hun beurt weer
functies van de tijd, dus uiteindelijk is de Lagrangiaan een geheel
tijdsafhankelijke functie. De actie 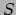 daarentegen is wel een constante,
omdat we de Lagrangiaan integreren over de tijd (elke functie geïntegreerd over
zijn variabele levert immers een constante op). De waarde van deze constante
hangt daarmee, uiteraard, geheel af van het pad
daarentegen is wel een constante,
omdat we de Lagrangiaan integreren over de tijd (elke functie geïntegreerd over
zijn variabele levert immers een constante op). De waarde van deze constante
hangt daarmee, uiteraard, geheel af van het pad 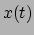 dat het deeltje volgt
tussen de twee tijdstippen
dat het deeltje volgt
tussen de twee tijdstippen 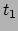 en
en 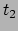 . Welk pad dit is, is precies de vraag
die wij beantwoord willen zien wanneer we mechanica doen. Als antwoord
postuleert het formalisme van Lagrange dat een deeltje altijd het pad
volgt dat de waarde van de actie minimaal of maximaal maakt. Dit noemt men
het principe van extreme actie, en levert een geheel nieuw voorschrift
om mechanica te doen: schrijf de Lagrangiaan op van bewegend deeltje,
integreer deze over de tijd, en zoek het pad dat deze integraal minimaal
of maximaal maakt.
. Welk pad dit is, is precies de vraag
die wij beantwoord willen zien wanneer we mechanica doen. Als antwoord
postuleert het formalisme van Lagrange dat een deeltje altijd het pad
volgt dat de waarde van de actie minimaal of maximaal maakt. Dit noemt men
het principe van extreme actie, en levert een geheel nieuw voorschrift
om mechanica te doen: schrijf de Lagrangiaan op van bewegend deeltje,
integreer deze over de tijd, en zoek het pad dat deze integraal minimaal
of maximaal maakt.
Deze manier van mechanica doen is soms te prefereren boven de meer
gebruikelijke wetten van Newton14.
Hij is echter niet minder fundamenteel: het is zowel mogelijk het principe van
extreme actie af te leiden door uit te gaan van de tweede
wet van Newton, als omgekeerd.
Het principe van extreme actie en de tweede wet van Newton
zijn daarom geheel equivalent.
Als voorbeeld van een toepassing van het formalisme van Lagrange, zal de
wet van Newton worden afgeleid door uit te gaan van het principe van
extreme actie. We beschouwen een deeltje met massa 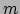 , dat beweegt onder
invloed van een kracht
, dat beweegt onder
invloed van een kracht 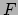 en daarom een potentiële energie
en daarom een potentiële energie 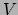 heeft
gerelateerd aan de kracht via
heeft
gerelateerd aan de kracht via
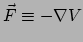 ; de kinetische
energie
; de kinetische
energie 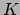 van een deeltje wordt, zoals altijd, gegeven door15
van een deeltje wordt, zoals altijd, gegeven door15
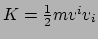 (waar
(waar
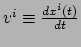 ). De Lagrangiaan
van dit deeltje wordt dan gegeven door
). De Lagrangiaan
van dit deeltje wordt dan gegeven door
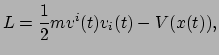 |
(26) |
en de actie 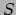 is dan
is dan
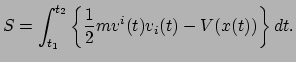 |
(27) |
Volgens het principe van extreme actie zal het deeltje een pad volgen dat
de actie een extreme waarde geeft. Dit leidt tot het volgende wiskundige
vraagstuk: gegeven een integraal over  met integrand
met integrand
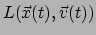 ,
hoe kan men dan bepalen welke functie
,
hoe kan men dan bepalen welke functie
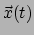 de uitkomst van deze
integraal minimaal of maximaal maakt? Het antwoord wordt gegeven door de
vergelijkingen van Euler-Lagrange: de componenten
de uitkomst van deze
integraal minimaal of maximaal maakt? Het antwoord wordt gegeven door de
vergelijkingen van Euler-Lagrange: de componenten 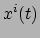 het pad
het pad
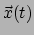 dat de integraal een extreme waarde geeft, voldoet aan
dat de integraal een extreme waarde geeft, voldoet aan
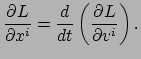 |
(28) |
Het bewijs van deze stelling is niet moeilijk, en gaat als volgt. Laten we
aannemen dat 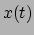 de
de 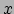 -component van het pad
-component van het pad
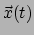 is dat de
integraal een extreme waarde geeft. Per definitie van een extreme waarde zal
elke kleine afwijking van dit pad,
is dat de
integraal een extreme waarde geeft. Per definitie van een extreme waarde zal
elke kleine afwijking van dit pad,
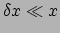 , de actie
, de actie 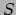 een extra
bijdrage geven,
een extra
bijdrage geven, 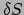 , die gelijk dient te zijn aan nul. We willen dus
op zoek naar het pad
, die gelijk dient te zijn aan nul. We willen dus
op zoek naar het pad 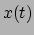 waarvoor geldt
waarvoor geldt
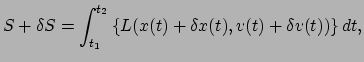 |
(29) |
waarin
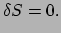 |
(30) |
Aangezien 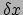 klein is, kunnen we de Lagrangiaan benaderen door16
klein is, kunnen we de Lagrangiaan benaderen door16
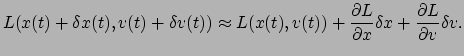 |
(31) |
Wanneer we dit invullen in vergelijking (29)
vinden we de actie 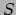 terug plus een extra term,
die we kunnen identificeren als
terug plus een extra term,
die we kunnen identificeren als 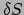 ,
,
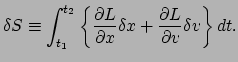 |
(32) |
Deze uitdrukking hoort gelijk te zijn aan nul. Nadat we een partiële
integratie17
doen op de tweede term van de integrand, wordt gevonden
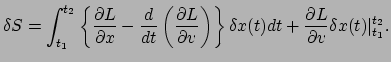 |
(33) |
De afwijking
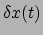 mag in principe elke mogelijke functie zijn, mits
maar geldt dat zij nul is op het begin en eind van het proces. Er geldt dan
ook
mag in principe elke mogelijke functie zijn, mits
maar geldt dat zij nul is op het begin en eind van het proces. Er geldt dan
ook
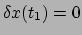 en
en
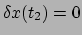 , en hiermee volgt dat de
laatste term in vergelijking (33)
gelijk is aan nul. De overgebleven integraal zal in het
algemeen gelijk kunnen zijn aan nul voor specifieke functies
, en hiermee volgt dat de
laatste term in vergelijking (33)
gelijk is aan nul. De overgebleven integraal zal in het
algemeen gelijk kunnen zijn aan nul voor specifieke functies
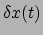 ;
echter, de eis is dat deze integraal nul is voor elke mogelijke afwijking
;
echter, de eis is dat deze integraal nul is voor elke mogelijke afwijking
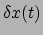 van het pad
van het pad 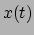 , en dit kan alleen wanneer alles tussen de
gekrulde haken gelijk is aan nul. Deze eis levert dan precies
vergelijking (28), voor de
, en dit kan alleen wanneer alles tussen de
gekrulde haken gelijk is aan nul. Deze eis levert dan precies
vergelijking (28), voor de
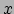 -component (waarvoor geldt
-component (waarvoor geldt 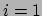 )
van het gezochte pad. Voor de twee andere plaatscoördinaten
van dit pad,
)
van het gezochte pad. Voor de twee andere plaatscoördinaten
van dit pad,
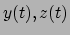 kan deze afleiding ook gebruikt worden en geldt
dezelfde uitkomst.
kan deze afleiding ook gebruikt worden en geldt
dezelfde uitkomst.
Wanneer de vergelijkingen van Euler-Lagrange toegepast wordt op de huidige
Lagrangiaan, vinden we
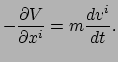 |
(34) |
De linkerkant van deze vergelijkingen herkennen we als de kracht 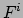 in de
in de 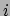 -richting,
terwijl de rechterkant precies gelijk is aan
-richting,
terwijl de rechterkant precies gelijk is aan
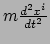 . We kunnen
deze drie uitkomsten samen nemen in een enkele vectorvergelijking,
. We kunnen
deze drie uitkomsten samen nemen in een enkele vectorvergelijking,
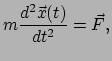 |
(35) |
wat precies de wet van Newton is. Zoals aangekondigd volgt deze inderdaad uit het
principe van extreme actie.
Het Lagrangiaanse formalisme kan ook gebruikt worden om de impuls van een deeltje
te bepalen. De impuls volgt uit de Lagrangiaan als
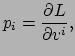 |
(36) |
wat voor de huidige Lagrangiaan de gebruikelijke uitdrukking voor de impuls
van een deeltje oplevert
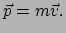 |
(37) |




Next: Het principe van Mach
Up: Klassieke mechanica
Previous: Gravitatie en getijdenkrachten
Contents
Jo van den Brand
2009-01-31
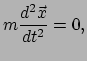
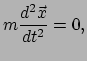
![]() .
Deze functie is gedefinieerd als het verschil tussen de kinetische energie
.
Deze functie is gedefinieerd als het verschil tussen de kinetische energie ![]() van een deeltje, en zijn potentiële energie
van een deeltje, en zijn potentiële energie ![]()
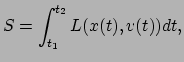
![]() , dat beweegt onder
invloed van een kracht
, dat beweegt onder
invloed van een kracht ![]() en daarom een potentiële energie
en daarom een potentiële energie ![]() heeft
gerelateerd aan de kracht via
heeft
gerelateerd aan de kracht via
![]() ; de kinetische
energie
; de kinetische
energie ![]() van een deeltje wordt, zoals altijd, gegeven door15
van een deeltje wordt, zoals altijd, gegeven door15
![]() (waar
(waar
![]() ). De Lagrangiaan
van dit deeltje wordt dan gegeven door
). De Lagrangiaan
van dit deeltje wordt dan gegeven door