



Next: De extra traagheid van
Up: De speciale relativiteitstheorie
Previous: Relativistisch Dopplereffect
Contents
Relativistische mechanica
De lagrangiaanse methode beschreven in sectie 2.8
leent zich uitstekend voor de uitbreiding van de
mechanica van Newton naar een versie die overeenkomt met het relativiteitsprincipe.
Allereerst zullen we
een vrij deeltje beschouwen, oftewel een deeltje met massa 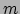 dat beweegt zonder
beïnvloed te worden door een kracht. De lagrangiaan voor een dergelijk deeltje bestaat
dan alleen uit een kinetische term,
dat beweegt zonder
beïnvloed te worden door een kracht. De lagrangiaan voor een dergelijk deeltje bestaat
dan alleen uit een kinetische term,
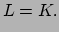 |
(195) |
In de klassieke mechanica wordt de kinetische energie gegeven door
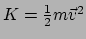 . Deze uitdrukking kunnen we echter niet overnemen
in de relativiteitstheorie. Immers, het relativiteitsprincipe eist dat de
natuurwetten zodanig geformuleerd dienen te worden, dat zij niet van vorm veranderen
wanneer naar een ander inertiaalstelsel wordt getransformeerd. Dit betekent
dat de gezochte lagrangiaan invariant moet zijn onder transformaties tussen
inertiaalstelsels, en daar voldoet bovenstaande uitdrukking zeker niet aan.
Echter, met enige aanpassing is een vorm te vinden die erg lijkt
op de oude uitdrukking, maar die wel degelijk invariant is. Hiervoor schrijven we
eerst de oude uitdrukking uit als
. Deze uitdrukking kunnen we echter niet overnemen
in de relativiteitstheorie. Immers, het relativiteitsprincipe eist dat de
natuurwetten zodanig geformuleerd dienen te worden, dat zij niet van vorm veranderen
wanneer naar een ander inertiaalstelsel wordt getransformeerd. Dit betekent
dat de gezochte lagrangiaan invariant moet zijn onder transformaties tussen
inertiaalstelsels, en daar voldoet bovenstaande uitdrukking zeker niet aan.
Echter, met enige aanpassing is een vorm te vinden die erg lijkt
op de oude uitdrukking, maar die wel degelijk invariant is. Hiervoor schrijven we
eerst de oude uitdrukking uit als
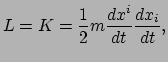 |
(196) |
waar Einstein's sommatieconventie gebruikt is:
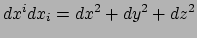 .
Wat de invariantie van deze uitdrukking in de weg staat zijn twee dingen: allereerst
zijn de
.
Wat de invariantie van deze uitdrukking in de weg staat zijn twee dingen: allereerst
zijn de 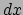 -en inertiaalstelsel-afhankelijk; ten tweede zijn de
-en inertiaalstelsel-afhankelijk; ten tweede zijn de 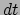 's dat eveneens.
We hadden immers al gezien dat waarnemers in verschillende inertiaalsystemen,
verschillende afstanden en tijdsduren meten. Deze uitdrukking kan daarom nooit
voldoen aan het relativiteitsprincipe. Echter, wanneer we
's dat eveneens.
We hadden immers al gezien dat waarnemers in verschillende inertiaalsystemen,
verschillende afstanden en tijdsduren meten. Deze uitdrukking kan daarom nooit
voldoen aan het relativiteitsprincipe. Echter, wanneer we 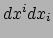 vervangen
door
vervangen
door
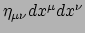 staat in de teller nu precies het lijnelement
staat in de teller nu precies het lijnelement
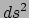 , waarvan bekend is dat dit invariant is. Op dezelfde manier ligt een
uitbreiding van de twee
, waarvan bekend is dat dit invariant is. Op dezelfde manier ligt een
uitbreiding van de twee 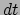 's ook voor de hand: vervang
's ook voor de hand: vervang 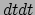 door
door 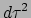 ,
zodat ook dit nu invariant is geworden. Een natuurlijke suggestie voor een
relativistische lagrangiaan van een vrij deeltje is dan
,
zodat ook dit nu invariant is geworden. Een natuurlijke suggestie voor een
relativistische lagrangiaan van een vrij deeltje is dan
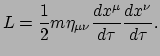 |
(197) |
Deze overwegingen zijn natuurlijk geen bewijs voor de geldigheid van
deze uitdrukking: het is een gok. Er zijn ook andere Lagrangianen denkbaar
die voldoen aan het relativiteitsprincipe. Echter, deze uitdrukking is
de meest eenvoudige, en bovendien zal blijken dat de bewegingswettem die hieruit
volgen, reduceren tot de oude vertrouwde bewegingswetten van Newton wanneer ze
toegepast worden in situaties waarbij snelheden veel lager zijn dan de lichtsnelheid.
Uiteindelijk zal het echter aan het experiment zijn om aan te tonen of de gevonden
wetmatigheden correct zijn. Tot nu toe wijzen alle experimenten uit dat dit
inderdaad het geval is.
De actie 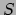 behorend bij deze lagrangiaan wordt verkregen door de lagrangiaan
te integreren over de tijd. Ook hier moet het relativiteitsprincipe in acht
worden genomen: de uitdrukking moet worden geïntegreerd over de eigentijd
behorend bij deze lagrangiaan wordt verkregen door de lagrangiaan
te integreren over de tijd. Ook hier moet het relativiteitsprincipe in acht
worden genomen: de uitdrukking moet worden geïntegreerd over de eigentijd
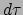 (in tegenstelling tot over de waarnemer-afhankelijke tijd
(in tegenstelling tot over de waarnemer-afhankelijke tijd 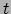 ) om zo
de invariantie van de actie te waarborgen. De actie wordt dan dus
) om zo
de invariantie van de actie te waarborgen. De actie wordt dan dus
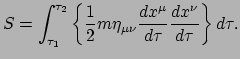 |
(198) |
Om de bewegingswet voor het deeltje af te leiden, dient het principe van
extreme actie weer te worden toegepast: er moet gezocht worden naar het pad
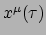 dat de waarde van deze integraal minimaal of maximaal maakt.
De Euler-Lagrange vergelijkingen voor deze situatie hebben de
vorm55
dat de waarde van deze integraal minimaal of maximaal maakt.
De Euler-Lagrange vergelijkingen voor deze situatie hebben de
vorm55
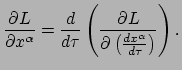 |
(199) |
Merk op dat dit vier vergelijkingen zijn: voor elk van de vier coordinaten van
het pad 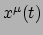 is er een vergelijking die moet worden opgelost.
Wanneer de relativistische lagrangiaan wordt ingevuld en beide zijden van de
Euler-Lagrange vergelijkingen worden uitgerekend, wordt gevonden dat een vrij
relativistisch deeltje een pad
is er een vergelijking die moet worden opgelost.
Wanneer de relativistische lagrangiaan wordt ingevuld en beide zijden van de
Euler-Lagrange vergelijkingen worden uitgerekend, wordt gevonden dat een vrij
relativistisch deeltje een pad
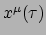 volgt waarvan de componenten
voldoen aan de vergelijkingen
volgt waarvan de componenten
voldoen aan de vergelijkingen
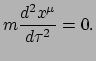 |
(200) |
Dit lijkt sprekend op de tweede wet van Newton voor een vrij deeltje, met twee
subtiele verschillen.
Ten eerste doet de wet van Newton uitspraken over de drie plaatscoördinaten
van het deeltje, waar deze nieuwe uitdrukking ook uitspraak doet over de tijd.
Deze laatste stelt dat
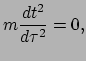 |
(201) |
waaruit volgt dat
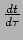 gelijk is aan een constante. Dat is niet
verrassend: we hadden immers al gezien dat de tijd
gelijk is aan een constante. Dat is niet
verrassend: we hadden immers al gezien dat de tijd 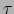 zoals gemeten door
een waarnemer die het deeltje stil ziet staan, een andere is dan de tijd
zoals gemeten door
een waarnemer die het deeltje stil ziet staan, een andere is dan de tijd
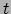 gemeten door een waarnemer die het deeltje ziet bewegen. Dit was precies
het tijddilatatie effect zoals besproken in sectie 5.3,
en de waarde van deze constante
laat zich dan ook aflezen van vergelijking (172):
het is precies de lorentzfactor
gemeten door een waarnemer die het deeltje ziet bewegen. Dit was precies
het tijddilatatie effect zoals besproken in sectie 5.3,
en de waarde van deze constante
laat zich dan ook aflezen van vergelijking (172):
het is precies de lorentzfactor 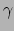 .
.
Figuur 44:
Ruimtetijddiagram in een specifiek lorentzframe dat de 3D ruimte
toont op 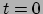 de viersnelheid
de viersnelheid 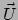 van een deeltje dat deze
3D ruimte passeert (op
van een deeltje dat deze
3D ruimte passeert (op 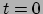 ), en twee 3D vectoren die in deze 3D ruimte
liggen: het ruimtelijke deel van de viersnelheid
), en twee 3D vectoren die in deze 3D ruimte
liggen: het ruimtelijke deel van de viersnelheid 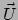 en de gewone
snelheid
en de gewone
snelheid 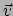 van het deeltje.
van het deeltje.
|
|
Het tweede verschil met de wet van Newton is het feit dat er hier afgeleiden
worden genomen naar de eigentijd 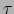 , waar in Newton's theorie afgeleiden
werden genomen naar de tijd
, waar in Newton's theorie afgeleiden
werden genomen naar de tijd 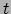 . Dit maakt van deze nieuwe afgeleide een
soort `gemengd-object': de gemeten afstanden
. Dit maakt van deze nieuwe afgeleide een
soort `gemengd-object': de gemeten afstanden 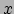 worden genomen zoals
gemeten door een willekeurige waarnemer ten opzichte van wie het deeltje
beweegt, waar de tijd gemeten wordt door de waarnemer die stilstaat ten opzichte
van het bewegende deeltje. Dit object wordt de viersnelheid
worden genomen zoals
gemeten door een willekeurige waarnemer ten opzichte van wie het deeltje
beweegt, waar de tijd gemeten wordt door de waarnemer die stilstaat ten opzichte
van het bewegende deeltje. Dit object wordt de viersnelheid 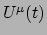 genoemd. Er geldt
genoemd. Er geldt
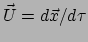 en voor de componenten geldt
en voor de componenten geldt
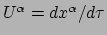 . Dit betekent voor de gewone snelheid
dat
. Dit betekent voor de gewone snelheid
dat
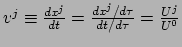 .
Deze relatie in combinatie met de normering van
.
Deze relatie in combinatie met de normering van 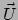 ,
,
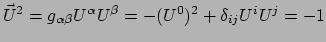 ,
betekent dat de componenten van de viersnelheid van de vorm
,
betekent dat de componenten van de viersnelheid van de vorm
 zijn. We vatten een en ander nog
een samen in Fig. 44. Het is nuttig om
zijn. We vatten een en ander nog
een samen in Fig. 44. Het is nuttig om 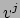 te zien als de
componenten van een 3D vector
te zien als de
componenten van een 3D vector 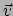 , de gewone snelheid, die leeft in
de 3D euclidische ruimte
, de gewone snelheid, die leeft in
de 3D euclidische ruimte
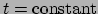 van het gekozen lorentzstelsel.
Deze 3D uimte is niet goed gedefinieerd totdat er een lorentzstelsel gekozen
is, en daarom hangt het bestaan van
van het gekozen lorentzstelsel.
Deze 3D uimte is niet goed gedefinieerd totdat er een lorentzstelsel gekozen
is, en daarom hangt het bestaan van 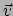 af van de specifieke keuze.
Op het moment dat een lorentzframe gekozen is, kunnen we
af van de specifieke keuze.
Op het moment dat een lorentzframe gekozen is, kunnen we 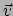 zien
als een coördinaten-onafhankelijk object.
zien
als een coördinaten-onafhankelijk object.
Teneinde weer contact te maken met de klassieke mechanica, schrijven we de viersnelheid
om naar een meer natuurlijk object (te weten: afstand en tijd
gemeten door een en dezelfde waarnemer). Dit kunnen we doen door te beseffen
dat de verlopen tijd gemeten door het deeltje, en die door een andere waarnemer,
met elkaar gerelateerd zijn via de formule van tijddilatatie:
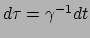 . Op deze manier is de gevonden wet uit te drukken als
. Op deze manier is de gevonden wet uit te drukken als
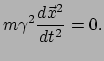 |
(202) |
De wet van Newton kan nu gezien worden als een speciaal geval van deze nieuwe
wet. Als we aannemen dat het deeltje veel langzamer beweegt dan het licht ten
opzichte van de waarnemer in wiens tijdsduur en afstand we nu alles hebben
uitgedrukt (oftewel we nemen aan dat 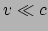 ), dan kan
vergelijking (208) benaderd worden door
), dan kan
vergelijking (208) benaderd worden door
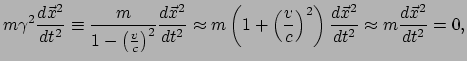 |
(203) |
waar gebruik is gemaakt van de wiskundige regel
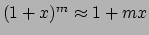 , welke
geldt als
, welke
geldt als 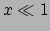 . Dit is precies de wet van Newton! Zo is nu aangetoond dat
de wet van Newton slechts een speciaal geval is van een meer algemene
bewegingswet, vergelijking (206)!
Dit geeft ons vertrouwen dat onze keuze voor de lagrangiaan
waarschijnlijk de juiste was: hij voldoet aan het relativiteitsprincipe, en
geeft ons bovendien onze oude vertrouwde bewegingswetten terug.
. Dit is precies de wet van Newton! Zo is nu aangetoond dat
de wet van Newton slechts een speciaal geval is van een meer algemene
bewegingswet, vergelijking (206)!
Dit geeft ons vertrouwen dat onze keuze voor de lagrangiaan
waarschijnlijk de juiste was: hij voldoet aan het relativiteitsprincipe, en
geeft ons bovendien onze oude vertrouwde bewegingswetten terug.
Met in het achterhoofd kunnen we nu verder gaan met het afleiden
van wetten betreffende de energie en impuls. Zoals besproken in sectie 2.8,
volgt een impuls uit een gegeven lagrangiaan via vergelijking (36).
Toegepast op de
relativistische lagrangiaan levert dit voor de impuls van het vrije deeltje
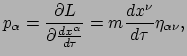 |
(204) |
en na beide kanten te contraheren met de inverse
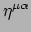 van
de minkowksimetriek wordt dit
van
de minkowksimetriek wordt dit
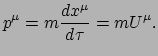 |
(205) |
Wederom lijkt dit erg op de impuls zoals bekend uit de mechanica van Newton:
een massa vermenigvuldigd met een snelheid. Echter, de snelheid is hier nu weer de
viersnelheid, en deze nieuwe impuls wordt dan ook de vierimpuls genoemd.
Vergeleken met de uitdrukking voor de newtoniaanse variant,
vergelijking (37), gaan weer
twee verschillen op: ten eerste is er een nul-component aanwezig, en ten
tweede is het weer een `gemengd-object': afgelegde afstand gemeten door een
willekeurige waarnemer, en tijdsduur gemeten door een waarnemer die stilstaat
ten opzichte van het deeltje. Het tweede verschil kunnen we weer een plaats
geven door de relatie tussen eigentijd en tijd te gebruiken. Dit levert
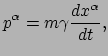 |
(206) |
en via dezelfde benaderingsmethode als gebruikt in vergelijking (209)
volgt direct dat
de 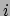 -component (
-component (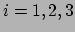 ) hiervan reduceert tot de impuls zoals bekend uit de
mechanica van Newton, wanneer het deeltje veel langzamer beweegt
dan het licht. De
) hiervan reduceert tot de impuls zoals bekend uit de
mechanica van Newton, wanneer het deeltje veel langzamer beweegt
dan het licht. De 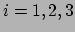 componenten van dit object worden daarom opgevat als
de relativistische uitdrukkingen van de impuls. Wat de nul-component
betreft, deze moet nog een interpretatie krijgen. Deze component is
componenten van dit object worden daarom opgevat als
de relativistische uitdrukkingen van de impuls. Wat de nul-component
betreft, deze moet nog een interpretatie krijgen. Deze component is
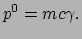 |
(207) |
Via een dimensie-analyse is meteen te zien dat het de dimensie van een
energie heeft, en dit wekt de suggestie dat het gaat om de energie van
het vrije deeltje. De vraag dringt zich dan al snel op: op welke manier
is deze uitdrukking gerelateerd aan de newtoniaanse uitdrukking voor de
energie van een vrij deeltje,
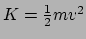 ? Ook hier biedt de
benadering van lage snelheden uitkomst. Er geldt
? Ook hier biedt de
benadering van lage snelheden uitkomst. Er geldt
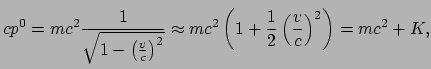 |
(208) |
waar de uitdrukking voor de newtoniaanse energie 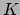 van een vrij deeltje
is ingevuld. Hier is nu gevolgd dat, in de benadering van lage snelheden,
de nul-component van de relativistische impuls reduceert tot de newtoniaanse
energie plus een extra term. Afgezien van deze constante term, is de
nul-component bij lage snelheden inderdaad gelijk aan de energie van het
deeltje zoals voorspeld door de newtoniaanse mechanica. Het ligt dan ook
voor de hand om aan te nemen dat we
van een vrij deeltje
is ingevuld. Hier is nu gevolgd dat, in de benadering van lage snelheden,
de nul-component van de relativistische impuls reduceert tot de newtoniaanse
energie plus een extra term. Afgezien van deze constante term, is de
nul-component bij lage snelheden inderdaad gelijk aan de energie van het
deeltje zoals voorspeld door de newtoniaanse mechanica. Het ligt dan ook
voor de hand om aan te nemen dat we 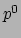 ook bij hoge snelheden mogen
opvatten als de energie van het deeltje. Wat de constante term betreft
kan de vraag worden gesteld hoe fysisch interessant deze is. Immers, in
de natuurkunde kennen alleen energieverschillen een meetbare
betekenis56,
en dus zal elke extra constante term toegevoegd aan de energie van een
systeem uit de berekening vallen wanneer een energieverschil opgeschreven
wordt. Toch heeft de constante term
ook bij hoge snelheden mogen
opvatten als de energie van het deeltje. Wat de constante term betreft
kan de vraag worden gesteld hoe fysisch interessant deze is. Immers, in
de natuurkunde kennen alleen energieverschillen een meetbare
betekenis56,
en dus zal elke extra constante term toegevoegd aan de energie van een
systeem uit de berekening vallen wanneer een energieverschil opgeschreven
wordt. Toch heeft de constante term 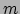 hier wel degelijk een fysische
betekenis: het is namelijk niet zomaar een willekeurige constante, het
is een constante die een eigenschap van het deeltje bevat (de massa)!
Deze energie is ook aanwezig wanneer het deeltje geen bewegingsenergie
heeft voor een gegeven waarnemer,
hier wel degelijk een fysische
betekenis: het is namelijk niet zomaar een willekeurige constante, het
is een constante die een eigenschap van het deeltje bevat (de massa)!
Deze energie is ook aanwezig wanneer het deeltje geen bewegingsenergie
heeft voor een gegeven waarnemer, 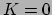 ; we spreken dan ook over rust-energie,
en deze is gelijk aan
; we spreken dan ook over rust-energie,
en deze is gelijk aan
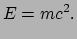 |
(209) |
Dit is wellicht de bekendste formule uit de natuurkunde. Hij zegt dat
elke massa een energie met zich meedraagt gelijk aan deze massa maal 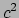 ,
en dat dit energie is die zich niet laat wegtransformeren door naar een
ander inertiaalstelsel te gaan. Het is daarom een fundamentele hoeveelheid
energie voor een gegeven massa
,
en dat dit energie is die zich niet laat wegtransformeren door naar een
ander inertiaalstelsel te gaan. Het is daarom een fundamentele hoeveelheid
energie voor een gegeven massa 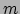 : voor alle waarnemers geldt dat
een massa op zijn minst deze hoeveelheid energie met zich meedraagt.
: voor alle waarnemers geldt dat
een massa op zijn minst deze hoeveelheid energie met zich meedraagt.
Resumerend is nu gevolgd dat onze keuze voor de lagrangiaan ons een
uitdrukking geeft voor de impuls, waarvan de 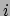 -componenten netjes reduceren
tot de impuls zoals die in de newtoniaanse mechanica bekend was; de
nul-component van de vierimpuls blijkt overeen te komen met de energie
van het deeltje. We schrijven dan ook
-componenten netjes reduceren
tot de impuls zoals die in de newtoniaanse mechanica bekend was; de
nul-component van de vierimpuls blijkt overeen te komen met de energie
van het deeltje. We schrijven dan ook
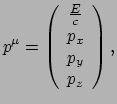 |
(210) |
waarin geldt
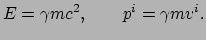 |
(211) |
De naam is niet de enige overeenkomst tussen de vierimpuls en viersnelheid: beide
transformeren op dezelfde manier tussen inertiaalsystemen. Met name de
lorentztransformaties werken op deze objecten op dezelfde manier; dit betekent dat
twee waarnemers die zich in de 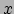 -richting met snelheid
-richting met snelheid 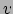 bewegen ten opzichte
van elkaar, verschillende energie (
bewegen ten opzichte
van elkaar, verschillende energie (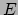 en
en 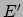 ) en impuls (
) en impuls (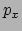 en
en 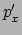 )
meten van een en hetzelfde deeltje, en dat deze zich tot elkaar verhouden als
)
meten van een en hetzelfde deeltje, en dat deze zich tot elkaar verhouden als
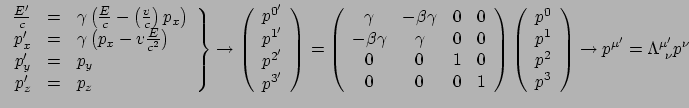 |
(212) |
Bovendien kunnen we de contractie
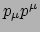 van de vierimpuls met zichzelf nemen,
omdat we al gezien hadden dat de contractie van een viervector met zichzelf
altijd een invariant oplevert. Het is dan eenvoudig om aan te tonen dat
deze invariant gelijk is, op een factor
van de vierimpuls met zichzelf nemen,
omdat we al gezien hadden dat de contractie van een viervector met zichzelf
altijd een invariant oplevert. Het is dan eenvoudig om aan te tonen dat
deze invariant gelijk is, op een factor 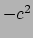 na, aan de massa van het
deeltje in het kwadraat. Er geldt
na, aan de massa van het
deeltje in het kwadraat. Er geldt
Dit leidt dan tot de volgende uitdrukking voor de relatie tussen de energie
en de impuls,
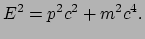 |
(214) |
Deze is bijna geheel57 equivalent aan de eerder
gevonden uitdrukking voor de relativistische energie,
vergelijking (214), maar is in de
praktijk soms te prefereren omdat deze ons in staat stelt de energie van een deeltje
uit te rekenen zonder de snelheid 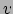 van het deeltje te hoeven kennen.
Met name in de deeltjesfysica, waar men vaak de impulsen van de deeltjes
beter kan meten dan louter hun snelheid, wordt deze formule veel gebruikt.
van het deeltje te hoeven kennen.
Met name in de deeltjesfysica, waar men vaak de impulsen van de deeltjes
beter kan meten dan louter hun snelheid, wordt deze formule veel gebruikt.
Het belang van energieën en impulsen in de relativiteitstheorie is dezelfde
als die in de Newtoniaanse mechanica. Daar is het een experimenteel gegeven
dat energie en impuls behouden grootheden zijn;
dit levert enorme voordelen op tijdens het berekenen van mechanische
processen. Het blijkt experimenteel dat dit nog steeds geldt voor onze nieuwe
uitdrukkingen voor de energie en impuls: elk experiment toont aan dat
deze twee grootheden niet veranderen tijdens fysische processen. Dit maakt
het uitermate handig om met energie en impuls te werken wanneer een
relativistisch probleem wordt beschouwd. Het is hier nu van belang om het
verschil tussen `behouden' en `invariant' te onderstrepen: een grootheid is
behouden wanneer geldt dat zijn waarde voor en na een proces dezelfde
is; een grootheid is invariant als geldt dat zijn waarde voor alle
waarnemers in verschillende inertiaalstelsels dezelfde is. Enkele voorbeelden:
de lichtsnelheid 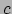 is een invariant en is behouden; de massa van een deeltje
is invariant maar in het algemeen niet behouden; de energie van een deeltje is
behouden maar niet invariant; snelheden zijn in het algemeen zowel niet behouden
als invariant.
is een invariant en is behouden; de massa van een deeltje
is invariant maar in het algemeen niet behouden; de energie van een deeltje is
behouden maar niet invariant; snelheden zijn in het algemeen zowel niet behouden
als invariant.
Nog enkele woorden over snelheden. Zoals al besproken, volgt uit de
minkowskimetriek de snelheidsregel van Einstein, waaruit we hebben laten volgen
dat het onmogelijk is een deeltje sneller te zien gaan dan het licht als het
voor een enkele waarnemer niet sneller gaat dan het licht. De vraag of
er een waarnemer bestaat voor wie het deeltje sneller gaat dan het licht is
nog niet aan de orde gekomen. Met de uitdrukking voor de relativistische
energie kan die vraag nu definitief worden beantwoord, en wel als volgt.
De uitdrukking gegeven in vergelijking (214)
voor de relativistische energie vertelt ons dat er in
een deeltje dat zich ten opzichte van ons met snelheid 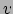 beweegt, een
energie
beweegt, een
energie 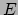 verscholen is. Omgekeerd kan de relatie ook gelezen worden
als de hoeveelheid energie benodigd om een deeltje vanuit stilstand tot
deze snelheid te versnellen. Als wij nu een deeltje naar de lichtsnelheid
willen versnellen, dan geldt
verscholen is. Omgekeerd kan de relatie ook gelezen worden
als de hoeveelheid energie benodigd om een deeltje vanuit stilstand tot
deze snelheid te versnellen. Als wij nu een deeltje naar de lichtsnelheid
willen versnellen, dan geldt 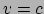 en wordt de noemer van vergelijking (214)
gelijk aan nul: de benodigde energie
en wordt de noemer van vergelijking (214)
gelijk aan nul: de benodigde energie 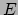 wordt oneindig groot. Dit is
een andere manier van zeggen dat het onmogelijk is een deeltje de
lichtsnelheid te geven! Hiermee is dan ook aangetoond dat deeltjes voor
deze waarnemer niet sneller kunnen gaan dan de lichtsnelheid; via
Einstein's snelheidsregel volgt dan direct dat geen enkele andere waarnemer
het deeltje sneller dan het licht kan zien bewegen.
wordt oneindig groot. Dit is
een andere manier van zeggen dat het onmogelijk is een deeltje de
lichtsnelheid te geven! Hiermee is dan ook aangetoond dat deeltjes voor
deze waarnemer niet sneller kunnen gaan dan de lichtsnelheid; via
Einstein's snelheidsregel volgt dan direct dat geen enkele andere waarnemer
het deeltje sneller dan het licht kan zien bewegen.
Er is een uitzondering op deze regel. Om tot de energie 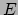 van
van 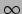 te komen, hebben we opgemerkt dat een deeltje met snelheid
te komen, hebben we opgemerkt dat een deeltje met snelheid 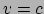 de
noemer in vergelijking (214)
gelijkmaakt aan nul, en delen door nul geeft oneindig.
Dit is inderdaad waar, mits de teller niet gelijk is aan nul. Als de
teller van een breuk ook gelijk is aan nul, levert delen door nul niet
altijd meer oneindig op. De waarde van de uitkomst is dan onbepaald:
afhankelijk van de context kan er iets eindigs uitkomen. Hier staat in de
teller van de breuk de massa van het deeltje, dus al met al ziet het ernaar
uit dat er wel degelijk deeltjes zouden kunnen bestaan die met precies de
lichtsnelheid bewegen mits de massa van zulke deeltjes maar gelijk is
aan nul58. Zulke deeltjes kennen we:
fotonen59 gaan met de
lichtsnelheid, en deze hebben inderdaad een massa gelijk aan nul. Dit volgt uit
alle metingen, maar het is interessant om te zien dat dit resultaat ook volgt
uit puur theoretische overwegingen. De impuls van een foton heeft de
waarde
de
noemer in vergelijking (214)
gelijkmaakt aan nul, en delen door nul geeft oneindig.
Dit is inderdaad waar, mits de teller niet gelijk is aan nul. Als de
teller van een breuk ook gelijk is aan nul, levert delen door nul niet
altijd meer oneindig op. De waarde van de uitkomst is dan onbepaald:
afhankelijk van de context kan er iets eindigs uitkomen. Hier staat in de
teller van de breuk de massa van het deeltje, dus al met al ziet het ernaar
uit dat er wel degelijk deeltjes zouden kunnen bestaan die met precies de
lichtsnelheid bewegen mits de massa van zulke deeltjes maar gelijk is
aan nul58. Zulke deeltjes kennen we:
fotonen59 gaan met de
lichtsnelheid, en deze hebben inderdaad een massa gelijk aan nul. Dit volgt uit
alle metingen, maar het is interessant om te zien dat dit resultaat ook volgt
uit puur theoretische overwegingen. De impuls van een foton heeft de
waarde
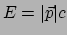 . Zoals elke keer weer blijkt dit een direct
gevolg te zijn van de minkowskimetriek en het relativiteitsprincipe!
. Zoals elke keer weer blijkt dit een direct
gevolg te zijn van de minkowskimetriek en het relativiteitsprincipe!
De vraag dient zich dan aan wat de waarde is van de energie van een foton: wat is hier
de uitkomst van nul gedeeld door nul? De uitdrukking voor de relativistische
energie doet geen uitspraak. Dit betekent niet dat er geen antwoord bestaat voor
de energie van een massaloos deeltje, maar alleen dat deze waarde niet door
vergelijking (214)
of door de relativiteitstheorie bepaald kan worden, en dat een andere formule
nodig is. In het geval van een foton is de formule bekend uit de quantummechanica,
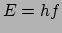 |
(215) |
waar 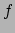 de frequentie (kleur) van het licht is, en
de frequentie (kleur) van het licht is, en 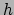 de constante van Planck.
De ontdekking van deze formule door Max Planck in 1900, was de start van de studie
van de quantummechanica. Samen met de ontdekking van de speciale relativiteitstheorie
leidde de ontwikkeling van de quantummechanica tot een gehele herschrijving van
de grondslagen van de natuurkunde.
de constante van Planck.
De ontdekking van deze formule door Max Planck in 1900, was de start van de studie
van de quantummechanica. Samen met de ontdekking van de speciale relativiteitstheorie
leidde de ontwikkeling van de quantummechanica tot een gehele herschrijving van
de grondslagen van de natuurkunde.




Next: De extra traagheid van
Up: De speciale relativiteitstheorie
Previous: Relativistisch Dopplereffect
Contents
Jo van den Brand
2009-01-31
![]() dat beweegt zonder
beïnvloed te worden door een kracht. De lagrangiaan voor een dergelijk deeltje bestaat
dan alleen uit een kinetische term,
dat beweegt zonder
beïnvloed te worden door een kracht. De lagrangiaan voor een dergelijk deeltje bestaat
dan alleen uit een kinetische term,
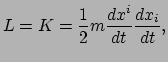
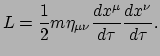
![]() behorend bij deze lagrangiaan wordt verkregen door de lagrangiaan
te integreren over de tijd. Ook hier moet het relativiteitsprincipe in acht
worden genomen: de uitdrukking moet worden geïntegreerd over de eigentijd
behorend bij deze lagrangiaan wordt verkregen door de lagrangiaan
te integreren over de tijd. Ook hier moet het relativiteitsprincipe in acht
worden genomen: de uitdrukking moet worden geïntegreerd over de eigentijd
![]() (in tegenstelling tot over de waarnemer-afhankelijke tijd
(in tegenstelling tot over de waarnemer-afhankelijke tijd ![]() ) om zo
de invariantie van de actie te waarborgen. De actie wordt dan dus
) om zo
de invariantie van de actie te waarborgen. De actie wordt dan dus
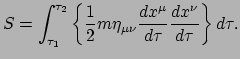
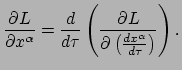
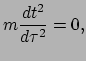
![\includegraphics[width=8cm]{Figures/u.eps}](img1055.png)
![]() , waar in Newton's theorie afgeleiden
werden genomen naar de tijd
, waar in Newton's theorie afgeleiden
werden genomen naar de tijd ![]() . Dit maakt van deze nieuwe afgeleide een
soort `gemengd-object': de gemeten afstanden
. Dit maakt van deze nieuwe afgeleide een
soort `gemengd-object': de gemeten afstanden ![]() worden genomen zoals
gemeten door een willekeurige waarnemer ten opzichte van wie het deeltje
beweegt, waar de tijd gemeten wordt door de waarnemer die stilstaat ten opzichte
van het bewegende deeltje. Dit object wordt de viersnelheid
worden genomen zoals
gemeten door een willekeurige waarnemer ten opzichte van wie het deeltje
beweegt, waar de tijd gemeten wordt door de waarnemer die stilstaat ten opzichte
van het bewegende deeltje. Dit object wordt de viersnelheid ![]() genoemd. Er geldt
genoemd. Er geldt
![]() en voor de componenten geldt
en voor de componenten geldt
![]() . Dit betekent voor de gewone snelheid
dat
. Dit betekent voor de gewone snelheid
dat
![]() .
Deze relatie in combinatie met de normering van
.
Deze relatie in combinatie met de normering van ![]() ,
,
![]() ,
betekent dat de componenten van de viersnelheid van de vorm
,
betekent dat de componenten van de viersnelheid van de vorm
![]() zijn. We vatten een en ander nog
een samen in Fig. 44. Het is nuttig om
zijn. We vatten een en ander nog
een samen in Fig. 44. Het is nuttig om ![]() te zien als de
componenten van een 3D vector
te zien als de
componenten van een 3D vector ![]() , de gewone snelheid, die leeft in
de 3D euclidische ruimte
, de gewone snelheid, die leeft in
de 3D euclidische ruimte
![]() van het gekozen lorentzstelsel.
Deze 3D uimte is niet goed gedefinieerd totdat er een lorentzstelsel gekozen
is, en daarom hangt het bestaan van
van het gekozen lorentzstelsel.
Deze 3D uimte is niet goed gedefinieerd totdat er een lorentzstelsel gekozen
is, en daarom hangt het bestaan van ![]() af van de specifieke keuze.
Op het moment dat een lorentzframe gekozen is, kunnen we
af van de specifieke keuze.
Op het moment dat een lorentzframe gekozen is, kunnen we ![]() zien
als een coördinaten-onafhankelijk object.
zien
als een coördinaten-onafhankelijk object.
![]() . Op deze manier is de gevonden wet uit te drukken als
. Op deze manier is de gevonden wet uit te drukken als
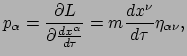
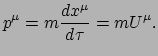
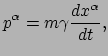
![]() -componenten netjes reduceren
tot de impuls zoals die in de newtoniaanse mechanica bekend was; de
nul-component van de vierimpuls blijkt overeen te komen met de energie
van het deeltje. We schrijven dan ook
-componenten netjes reduceren
tot de impuls zoals die in de newtoniaanse mechanica bekend was; de
nul-component van de vierimpuls blijkt overeen te komen met de energie
van het deeltje. We schrijven dan ook
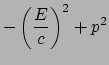
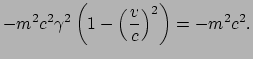
![]() is een invariant en is behouden; de massa van een deeltje
is invariant maar in het algemeen niet behouden; de energie van een deeltje is
behouden maar niet invariant; snelheden zijn in het algemeen zowel niet behouden
als invariant.
is een invariant en is behouden; de massa van een deeltje
is invariant maar in het algemeen niet behouden; de energie van een deeltje is
behouden maar niet invariant; snelheden zijn in het algemeen zowel niet behouden
als invariant.
![]() beweegt, een
energie
beweegt, een
energie ![]() verscholen is. Omgekeerd kan de relatie ook gelezen worden
als de hoeveelheid energie benodigd om een deeltje vanuit stilstand tot
deze snelheid te versnellen. Als wij nu een deeltje naar de lichtsnelheid
willen versnellen, dan geldt
verscholen is. Omgekeerd kan de relatie ook gelezen worden
als de hoeveelheid energie benodigd om een deeltje vanuit stilstand tot
deze snelheid te versnellen. Als wij nu een deeltje naar de lichtsnelheid
willen versnellen, dan geldt ![]() en wordt de noemer van vergelijking (214)
gelijk aan nul: de benodigde energie
en wordt de noemer van vergelijking (214)
gelijk aan nul: de benodigde energie ![]() wordt oneindig groot. Dit is
een andere manier van zeggen dat het onmogelijk is een deeltje de
lichtsnelheid te geven! Hiermee is dan ook aangetoond dat deeltjes voor
deze waarnemer niet sneller kunnen gaan dan de lichtsnelheid; via
Einstein's snelheidsregel volgt dan direct dat geen enkele andere waarnemer
het deeltje sneller dan het licht kan zien bewegen.
wordt oneindig groot. Dit is
een andere manier van zeggen dat het onmogelijk is een deeltje de
lichtsnelheid te geven! Hiermee is dan ook aangetoond dat deeltjes voor
deze waarnemer niet sneller kunnen gaan dan de lichtsnelheid; via
Einstein's snelheidsregel volgt dan direct dat geen enkele andere waarnemer
het deeltje sneller dan het licht kan zien bewegen.
![]() van
van ![]() te komen, hebben we opgemerkt dat een deeltje met snelheid
te komen, hebben we opgemerkt dat een deeltje met snelheid ![]() de
noemer in vergelijking (214)
gelijkmaakt aan nul, en delen door nul geeft oneindig.
Dit is inderdaad waar, mits de teller niet gelijk is aan nul. Als de
teller van een breuk ook gelijk is aan nul, levert delen door nul niet
altijd meer oneindig op. De waarde van de uitkomst is dan onbepaald:
afhankelijk van de context kan er iets eindigs uitkomen. Hier staat in de
teller van de breuk de massa van het deeltje, dus al met al ziet het ernaar
uit dat er wel degelijk deeltjes zouden kunnen bestaan die met precies de
lichtsnelheid bewegen mits de massa van zulke deeltjes maar gelijk is
aan nul58. Zulke deeltjes kennen we:
fotonen59 gaan met de
lichtsnelheid, en deze hebben inderdaad een massa gelijk aan nul. Dit volgt uit
alle metingen, maar het is interessant om te zien dat dit resultaat ook volgt
uit puur theoretische overwegingen. De impuls van een foton heeft de
waarde
de
noemer in vergelijking (214)
gelijkmaakt aan nul, en delen door nul geeft oneindig.
Dit is inderdaad waar, mits de teller niet gelijk is aan nul. Als de
teller van een breuk ook gelijk is aan nul, levert delen door nul niet
altijd meer oneindig op. De waarde van de uitkomst is dan onbepaald:
afhankelijk van de context kan er iets eindigs uitkomen. Hier staat in de
teller van de breuk de massa van het deeltje, dus al met al ziet het ernaar
uit dat er wel degelijk deeltjes zouden kunnen bestaan die met precies de
lichtsnelheid bewegen mits de massa van zulke deeltjes maar gelijk is
aan nul58. Zulke deeltjes kennen we:
fotonen59 gaan met de
lichtsnelheid, en deze hebben inderdaad een massa gelijk aan nul. Dit volgt uit
alle metingen, maar het is interessant om te zien dat dit resultaat ook volgt
uit puur theoretische overwegingen. De impuls van een foton heeft de
waarde
![]() . Zoals elke keer weer blijkt dit een direct
gevolg te zijn van de minkowskimetriek en het relativiteitsprincipe!
. Zoals elke keer weer blijkt dit een direct
gevolg te zijn van de minkowskimetriek en het relativiteitsprincipe!