



Next: Witte dwergen, supernovae en
Up: Quantumfysische verschijnselen in het
Previous: Nucleosynthese in sterren
Contents
Het standaard zonnemodel (standard solar model - SSM) is een van de meest
complete en succesvolle theorieën van de moderne sterrenkunde. We zullen
de basisgedachten achter dit model en de consequenties ervan kort bespreken.
Het SSM is gebaseerd op vier aannamen:
- De zon is sferisch symmetrisch.
- De zon is in hydrostatisch evenwicht.
- Energie wordt overgebracht door straling en convectie alsook
door neutrino's.
- Fusie van waterstof in helium is de energiebron.
De centripetale versnelling op de equator van de zon is
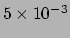 m/s
m/s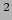 en dat is verwaarloosbaar ten opzichte van haar gravitatie van 274 m/s
en dat is verwaarloosbaar ten opzichte van haar gravitatie van 274 m/s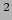 .
Sferische symmetrie is dus een goede aanname en we mogen toestandvariabelen, zoals temperatuur
en druk, schrijven als functie van de afstand tot het centrum van de zon,
bijvoorbeeld
.
Sferische symmetrie is dus een goede aanname en we mogen toestandvariabelen, zoals temperatuur
en druk, schrijven als functie van de afstand tot het centrum van de zon,
bijvoorbeeld 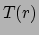 en
en 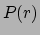 . Indien de lokale compositie (voornamelijk
waterstof en helium) bekend is, dan geven deze twee grootheden ook de dichtheid.
Als we aannemen dat de gasdruk22
dominant is over de stralingsdruk dan kunnen
we deze laatste verwaarlozen. Er geldt
. Indien de lokale compositie (voornamelijk
waterstof en helium) bekend is, dan geven deze twee grootheden ook de dichtheid.
Als we aannemen dat de gasdruk22
dominant is over de stralingsdruk dan kunnen
we deze laatste verwaarlozen. Er geldt
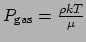 en
en
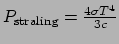 , met
, met 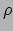 de dichtheid,
de dichtheid,
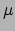 de deeltjesmassa (
de deeltjesmassa (
 kg voor waterstofmoleculen),
kg voor waterstofmoleculen),
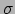 de Stefan-Boltzmann constante en
de Stefan-Boltzmann constante en 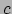 de
lichtsnelheid. Diep in de zon bedraagt de dichtheid
de
lichtsnelheid. Diep in de zon bedraagt de dichtheid
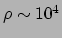 kg/m
kg/m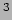 en temperatuur
en temperatuur
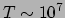 K en
onder deze condities vinden we
K en
onder deze condities vinden we
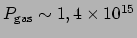 en
en
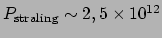 N/m
N/m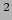 . We zien dat de stralingsdruk
inderdaad verwaarloosbaar is23.
. We zien dat de stralingsdruk
inderdaad verwaarloosbaar is23.
Figuur 12:
In de zon is er evenwicht tussen gravitatie en de gasdruk ten gevolge van de
energie opgewekt door kernfusie. Rechts: op een schil met oppervlak 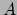 en dikte
en dikte 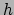 is er
hydrostatisch evenwicht tussen de krachten.
is er
hydrostatisch evenwicht tussen de krachten.
|
|
We stellen ons voor dat de zon is opgebouwd uit sferische schillen. Op de bodem van
een volume element werkt een kracht ter grootte
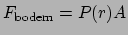 , terwijl
op de top een kracht werkt ter grootte
, terwijl
op de top een kracht werkt ter grootte
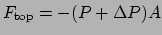 . Het minteken
geeft aan dat de kracht naar het centrum van de zon wijst. Verder werkt er nog
de gravitatie op de massa van het volume element. Het gewicht is gelijk aan
. Het minteken
geeft aan dat de kracht naar het centrum van de zon wijst. Verder werkt er nog
de gravitatie op de massa van het volume element. Het gewicht is gelijk aan
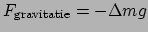 , met
, met 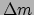 de massa van het element en
de massa van het element en 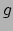 de lokale gravitatie versnelling. We vinden
de lokale gravitatie versnelling. We vinden
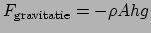 .
De lokale gravitatie wordt gegeven door
.
De lokale gravitatie wordt gegeven door
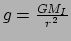 , waarbij
, waarbij 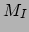 de totale massa binnen de bol is die begrensd wordt door de sferische schil.
Deze krachten zijn in hydrostatisch evenwicht,
de totale massa binnen de bol is die begrensd wordt door de sferische schil.
Deze krachten zijn in hydrostatisch evenwicht,
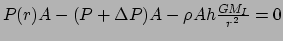 , en er geldt voor een dunne
sferische schil (met
, en er geldt voor een dunne
sferische schil (met
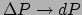 en
en
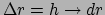 )
)
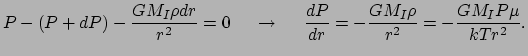 |
(50) |
Als randvoorwaarde hebben we dat de druk nul moet zijn aan de rand van de ster,
waar
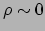 . De massa binnen de bol bedraagt
. De massa binnen de bol bedraagt 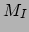 en de sferische
schil levert een bijdrage
en de sferische
schil levert een bijdrage
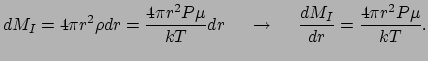 |
(51) |
Hier geldt de randvoorwaarde dat 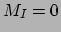 als
als 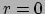 . Verder geldt dat
. Verder geldt dat
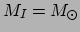 als
als 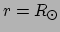 , de straal van de ster.
, de straal van de ster.
In de evenwichttoestand is de energie binnen het volume element, tussen 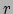 en
en 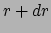 constant. De stralingsflux door het buiten oppervlak is dan gelijk
aan de som van de flux door het binnen oppervlak en het vermogen dat binnen
de sferische schil wordt gegenereerd. Dit geeft
constant. De stralingsflux door het buiten oppervlak is dan gelijk
aan de som van de flux door het binnen oppervlak en het vermogen dat binnen
de sferische schil wordt gegenereerd. Dit geeft
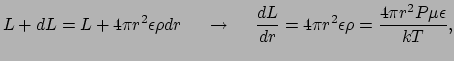 |
(52) |
met 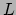 de luminositeit ofwel de flux van uitgestraalde energie per
tijdseenheid, en
de luminositeit ofwel de flux van uitgestraalde energie per
tijdseenheid, en 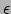 de functie van intrinsieke energie generatie (in W/kg).
Bij een hogere temperature zal er meer energie in de ster worden gegenereerd.
Als randvoorwaarden gebruiken we
de functie van intrinsieke energie generatie (in W/kg).
Bij een hogere temperature zal er meer energie in de ster worden gegenereerd.
Als randvoorwaarden gebruiken we 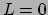 als
als 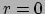 , terwijl voor
, terwijl voor 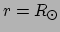 we
de luminositeit
we
de luminositeit 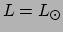 van de zon dienen te vinden.
van de zon dienen te vinden.
Tenslotte stellen we een vergelijking op voor
de temperatuurverdeling van de zon. Hiertoe beschouwen
we de intensiteit (J/(m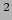 s)) door een sferische schil. Straling passeert
deze schil, terwijl er ook straling door kernfusie in de schil kan worden
gegenereerd. Als de gemiddelde intensiteit van de straling binnen de schil
gelijk is aan
s)) door een sferische schil. Straling passeert
deze schil, terwijl er ook straling door kernfusie in de schil kan worden
gegenereerd. Als de gemiddelde intensiteit van de straling binnen de schil
gelijk is aan 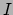 , dan is de energie die geabsorbeerd wordt per tijdseenheid
voor straling die de schil passeert gelijk aan
, dan is de energie die geabsorbeerd wordt per tijdseenheid
voor straling die de schil passeert gelijk aan
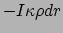 , met
, met 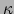 de opaciteit gedefinieerd als
de opaciteit gedefinieerd als
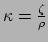 , met
, met 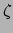 de lineaire absorptie coëfficiënt. De geabsorbeerde intensiteit
bedraagt
de lineaire absorptie coëfficiënt. De geabsorbeerde intensiteit
bedraagt
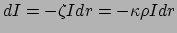 . De intensiteit van de straling
die de schil passeert is gerelateerd aan de lokale luminositeit volgens
. De intensiteit van de straling
die de schil passeert is gerelateerd aan de lokale luminositeit volgens
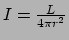 . Vanwege de relatie tussen energie (
. Vanwege de relatie tussen energie (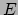 ) en impuls
(
) en impuls
(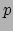 voor straling geldt
voor straling geldt 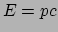 , kunnen we de impulsverandering per tijdseenheid
van de straling tussen binnen en buiten oppervlak schrijven als
, kunnen we de impulsverandering per tijdseenheid
van de straling tussen binnen en buiten oppervlak schrijven als
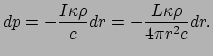 |
(53) |
De impulsverandering in een sectie met eenheidsoppervlak vertegenwoordigt
een krachtverschil per eenheid van oppervlakte, of stralingsdruk tussen en
binnen en buiten oppervlak van het element. Er geldt
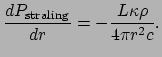 |
(54) |
Omdat de stralingsdruk gegeven wordt door
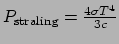 ,
kunnen we dit differentiëren naar
,
kunnen we dit differentiëren naar 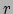 en in bovenstaande vergelijking invullen.
We vinden dan
en in bovenstaande vergelijking invullen.
We vinden dan
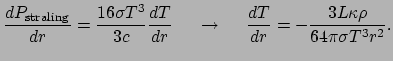 |
(55) |
Voor de temperatuur nemen we als randvoorwaarde
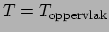 als
als
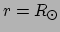 . Dat is de conventionele temperatuur van een ster, die men
kan waarnemen; het is de temperatuur van de fotosfeer, de zichtbare buitenkant
van de ster.
. Dat is de conventionele temperatuur van een ster, die men
kan waarnemen; het is de temperatuur van de fotosfeer, de zichtbare buitenkant
van de ster.
Figuur 13:
Resultaten van het standaard model voor de zon. Boven: temperatuur en
dichtheidsverdeling; onder: massafracties van diverse elementen.
|
|
Bovenstaande differentiaalvergelijkigen kunnen iteratief worden opgelost
en Fig. 13 geeft de berekende temperatuur en dichtheidsverdeling in de zon.
We zien dat in het centrum van de zon een temperatuur van 16 miljoen graden
wordt bereikt.
We kunnen een gevoel krijgen voor het verband tussen massa (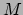 ), grootte (
), grootte (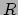 )
en de druk (
)
en de druk (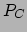 ) in het binnenste van de ster. Hiervoor gebruiken we vergelijking
(53) om bij grove benadering de druk in de
ster (in één stap met
) in het binnenste van de ster. Hiervoor gebruiken we vergelijking
(53) om bij grove benadering de druk in de
ster (in één stap met
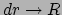 en
en
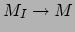 ) te schrijven als
) te schrijven als
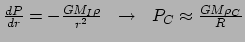 . We benaderen de massa met
. We benaderen de massa met
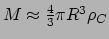 . Combineren levert
. Combineren levert
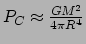 . Op dezelfde wijze vinden
we dat de centrale temperature schaalt als
. Op dezelfde wijze vinden
we dat de centrale temperature schaalt als
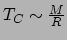 .
.
Als we sterren met globaal dezelfde massa 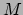 beschouwen, dan
geldt
beschouwen, dan
geldt
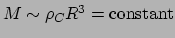 . Omdat dus geldt dat
. Omdat dus geldt dat
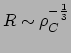 , vinden we de toestandsvergelijking
voor de centrale druk
, vinden we de toestandsvergelijking
voor de centrale druk
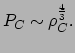 |
(56) |
Dit is de toestandsvergelijking voor een ster waarbij de druk precies in balans
is met de gravitatie. Toestandsvergelijking van de vorm
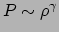 worden polytropische toestandsvergelijkingen genoemd. Als de polytropische
index
worden polytropische toestandsvergelijkingen genoemd. Als de polytropische
index 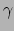 groter is dan
groter is dan 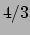 dan neemt de druk
sneller toe bij compressie en stoot de ster terug, de ster is stabiel.
Toestandsvergelijkingen met
dan neemt de druk
sneller toe bij compressie en stoot de ster terug, de ster is stabiel.
Toestandsvergelijkingen met
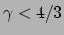 zijn niet stabiel.
zijn niet stabiel.




Next: Witte dwergen, supernovae en
Up: Quantumfysische verschijnselen in het
Previous: Nucleosynthese in sterren
Contents
Jo van den Brand
2009-01-31
![\includegraphics[width=12cm]{Figures/he.eps}](img376.png)
![\includegraphics[width=12cm]{Figures/he.eps}](img376.png)
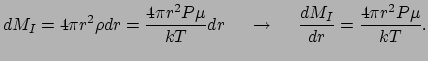
![]() en
en ![]() constant. De stralingsflux door het buiten oppervlak is dan gelijk
aan de som van de flux door het binnen oppervlak en het vermogen dat binnen
de sferische schil wordt gegenereerd. Dit geeft
constant. De stralingsflux door het buiten oppervlak is dan gelijk
aan de som van de flux door het binnen oppervlak en het vermogen dat binnen
de sferische schil wordt gegenereerd. Dit geeft
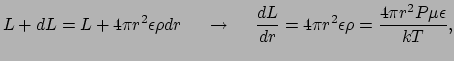
![]() s)) door een sferische schil. Straling passeert
deze schil, terwijl er ook straling door kernfusie in de schil kan worden
gegenereerd. Als de gemiddelde intensiteit van de straling binnen de schil
gelijk is aan
s)) door een sferische schil. Straling passeert
deze schil, terwijl er ook straling door kernfusie in de schil kan worden
gegenereerd. Als de gemiddelde intensiteit van de straling binnen de schil
gelijk is aan ![]() , dan is de energie die geabsorbeerd wordt per tijdseenheid
voor straling die de schil passeert gelijk aan
, dan is de energie die geabsorbeerd wordt per tijdseenheid
voor straling die de schil passeert gelijk aan
![]() , met
, met ![]() de opaciteit gedefinieerd als
de opaciteit gedefinieerd als
![]() , met
, met ![]() de lineaire absorptie coëfficiënt. De geabsorbeerde intensiteit
bedraagt
de lineaire absorptie coëfficiënt. De geabsorbeerde intensiteit
bedraagt
![]() . De intensiteit van de straling
die de schil passeert is gerelateerd aan de lokale luminositeit volgens
. De intensiteit van de straling
die de schil passeert is gerelateerd aan de lokale luminositeit volgens
![]() . Vanwege de relatie tussen energie (
. Vanwege de relatie tussen energie (![]() ) en impuls
(
) en impuls
(![]() voor straling geldt
voor straling geldt ![]() , kunnen we de impulsverandering per tijdseenheid
van de straling tussen binnen en buiten oppervlak schrijven als
, kunnen we de impulsverandering per tijdseenheid
van de straling tussen binnen en buiten oppervlak schrijven als
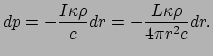
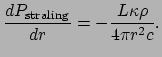
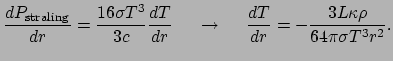
![\includegraphics[width=12cm]{Figures/ssm.eps}](img412.png)
![]() ), grootte (
), grootte (![]() )
en de druk (
)
en de druk (![]() ) in het binnenste van de ster. Hiervoor gebruiken we vergelijking
(53) om bij grove benadering de druk in de
ster (in één stap met
) in het binnenste van de ster. Hiervoor gebruiken we vergelijking
(53) om bij grove benadering de druk in de
ster (in één stap met
![]() en
en
![]() ) te schrijven als
) te schrijven als
![]() . We benaderen de massa met
. We benaderen de massa met
![]() . Combineren levert
. Combineren levert
![]() . Op dezelfde wijze vinden
we dat de centrale temperature schaalt als
. Op dezelfde wijze vinden
we dat de centrale temperature schaalt als
![]() .
.
![]() beschouwen, dan
geldt
beschouwen, dan
geldt
![]() . Omdat dus geldt dat
. Omdat dus geldt dat
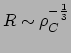 , vinden we de toestandsvergelijking
voor de centrale druk
, vinden we de toestandsvergelijking
voor de centrale druk