De tweede belangrijke stap in de ontwikkeling van de differentiaalmeetkunde
werd gezet door B. Riemann (1826 - 1866) in een colloqium, gehouden op 10
juni 1854, voor de filosofische faculteit van de universiteit van Göttingen,
waarvan de titel luidde `Ueber die hypothesen welche der Geometrie zu Grunde
liegen'. Hierin gaf hij aan hoe een twee-dimensionaal gekromd oppervlak kan
worden gegeneraliseerd tot `eind n fach ausgedehnte Mänigfaltigkeit' en
bovendien introduceerde hij een afstandsbegrip voor de ![]() -dimensionale
ruimte (riemannse meetkunde). De `n fach ausgedehnte Mänigfaltigkeit' is wat
tegenwoordig een
-dimensionale
ruimte (riemannse meetkunde). De `n fach ausgedehnte Mänigfaltigkeit' is wat
tegenwoordig een ![]() -dimensionale differentieerbare variëteit wordt genoemd.
-dimensionale differentieerbare variëteit wordt genoemd.
De generalisatie is als volgt: Gauss beschreef de punten van een
twee-dimensionaal oppervlak met behulp van een tweetal reële coördinaten
![]() . Riemann beschreef de punten van een
. Riemann beschreef de punten van een
![]() -dimensionale differentieerbare variëteit met behulp van reële
coördinaten
-dimensionale differentieerbare variëteit met behulp van reële
coördinaten
![]() . Bij Gauss is de afstand tussen twee
infinitesimaal verwijderde punten
. Bij Gauss is de afstand tussen twee
infinitesimaal verwijderde punten
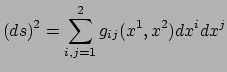 |
(425) |
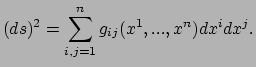 |
(426) |
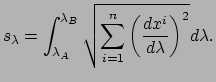 |
(428) |
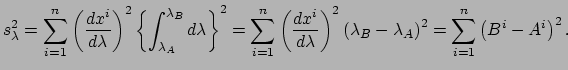 |
(429) |
Een verdere belangrijke bijdrage van Riemann is zijn generalisatie van de
kromming van Gauss tot een ![]() -dimensionale ruimte: de
krommingstensor van Riemann. De krommingstensor speelt een uitermate
belangrijke rol in Einstein's gravitatietheorie.
-dimensionale ruimte: de
krommingstensor van Riemann. De krommingstensor speelt een uitermate
belangrijke rol in Einstein's gravitatietheorie.