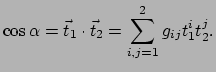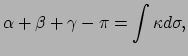Next: Riemannse meetkunde
Up: Appendix - Meetkunde
Previous: Appendix - Meetkunde
Contents
Uit brieven blijkt dat C.F. Gauss (1777 - 1855) al in 1824 een vergaand
inzicht in de niet-euclidische meetkunde had. Hij maakte dit echter niet
publiek omdat hij hiervan teveel opschudding verwachtte. De niet-euclidische meetkunde
werd ook onafhankelijk door J. Bolyai (1802 - 1860) en N.I. Lobachevski (1793 - 1856)
geformuleerd.
Figuur 57:
De raakvector in een punt van een kromme. Voor
 naders
naders
 tot de raakvector.
tot de raakvector.
|
|
Fig. 57 toont dat
een kromme is voor te stellen door de vergelijking
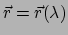 ,
met
,
met 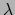 de parameter van de kromme. Voor de componenten
de parameter van de kromme. Voor de componenten 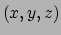 van
de vector
van
de vector 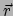 geldt
geldt
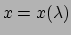 ,
,
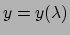 en
en
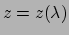 .
Een raakvector aan de kromme wordt gegeven door
.
Een raakvector aan de kromme wordt gegeven door
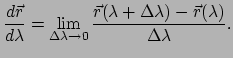 |
(400) |
De booglengte langs de kromme tussen de punten
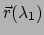 en
en
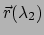 wordt gegeven door
wordt gegeven door
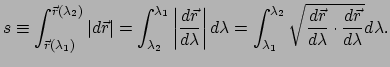 |
(401) |
De booglengte 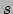 tot een vast punt op de kromme is ook te gebruiken als parameter
in plaats van
tot een vast punt op de kromme is ook te gebruiken als parameter
in plaats van 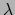 , immer
, immer
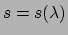 . Men schrijft
. Men schrijft
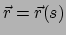 ,
en de raakvector is dan
,
en de raakvector is dan
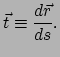 |
(402) |
Merk op dat dit een eenheidsvector is,
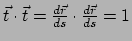 , omdat
, omdat
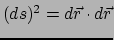 .
Uit
.
Uit
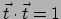 volgt door differentiatie naar
volgt door differentiatie naar  , dat
, dat
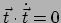 ,
zodat
,
zodat
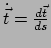 loodrecht op
loodrecht op 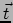 , dus op de raaklijn staat.
De hoofdnormaal
, dus op de raaklijn staat.
De hoofdnormaal 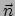 is per definitie de eenheidsvector in de richting van
is per definitie de eenheidsvector in de richting van
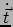 , dus
, dus
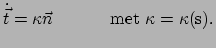 |
(403) |
Uit het bovenstaande volgt
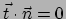 en uit vergelijking (409)
met
en uit vergelijking (409)
met
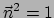 , dat
, dat
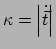 , waarbij
, waarbij 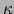 de
kromming van de curve is. Tenslotte wordt de binormaal
de
kromming van de curve is. Tenslotte wordt de binormaal 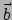 gedefinieerd door
gedefinieerd door
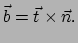 |
(404) |
Figuur:
Meebewegend orthonormaal coördinatenstelsel
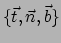 van een kromme.
De triade bestaat uit de tangentvector
van een kromme.
De triade bestaat uit de tangentvector 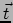 , de normaalvector
, de normaalvector 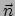 en de binormaalvector
en de binormaalvector
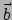 .
.
|
|
Fig. 58 toont dat in
ieder punt 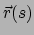 van de kromme er nu een drietal vectoren
van de kromme er nu een drietal vectoren
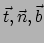 bestaat.
Dit stelsel heet de meebewegende triade. Ze vormen een orthonormaal stelsel.
bestaat.
Dit stelsel heet de meebewegende triade. Ze vormen een orthonormaal stelsel.
Uit vergelijking (
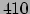 ) volgt
) volgt
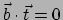 . Differentiatie naar
. Differentiatie naar 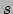 geeft, met vergelijkingen (
geeft, met vergelijkingen (
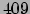 ) en (
) en (
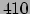 )
)
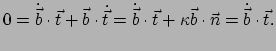 |
(405) |
Uit
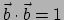 volgt
volgt
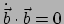 en we zien
dat
en we zien
dat
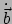 parallel is aan vector
parallel is aan vector 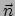 . Men definieert
. Men definieert
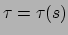 met
met
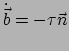 , waarbij
, waarbij 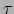 de torsie van de kromme wordt genoemd.
Tenslotte volgt uit
de torsie van de kromme wordt genoemd.
Tenslotte volgt uit
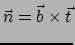 dat
dat
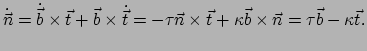 |
(406) |
Samenvattend geldt
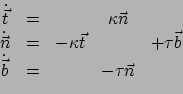 |
(407) |
en dit zijn de formules van Frenet (1847) en Serret (1850). Een gevolg hiervan is dat
bij gegeven kromming en torsie door integratie van deze eerste-orde differentiaalvergelijkingen
de kromme op een verplaatsing na (integratieconstanten) vastligt.
Figuur 59:
Kromme door punt  in het oppervlak
in het oppervlak  . Beschouw alle krommen
door
. Beschouw alle krommen
door 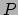 . De verzameling van alle raakvectoren in
. De verzameling van alle raakvectoren in 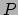 van al deze krommen
vormt de tangentenvectorruimte
van al deze krommen
vormt de tangentenvectorruimte 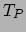 .
.
|
|
Vervolgens beschouwen we gebogen oppervlakken in 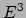 . In de tijd voor Gauss
werd een gebogen oppervlak voorgesteld door
. In de tijd voor Gauss
werd een gebogen oppervlak voorgesteld door
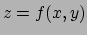 of
of
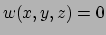 . In het
bijzonder kan men krommen in een dergelijk oppervlak beschouwen en voor deze
krommen kan men uiteraard de bovenstaande begrippen invoeren.
Fig. 59 toont dat
. In het
bijzonder kan men krommen in een dergelijk oppervlak beschouwen en voor deze
krommen kan men uiteraard de bovenstaande begrippen invoeren.
Fig. 59 toont dat 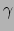 een
kromme in het oppervlak
een
kromme in het oppervlak 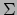 is met
is met 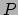 een punt op
een punt op 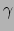 . Dan heeft
. Dan heeft 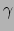 een raakvector
een raakvector
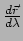 in het punt
in het punt 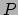 . Beschouw nu alle mogelijke
krommen in
. Beschouw nu alle mogelijke
krommen in 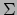 door
door 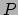 , dan vormt de verzameling van alle bijbehorende
raakvectoren
, dan vormt de verzameling van alle bijbehorende
raakvectoren
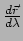 een twee-dimensionale vectorruimte
een twee-dimensionale vectorruimte 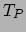 ,
de raakvectorruimte, tangentenvectorruimte of raakvlak genoemd. De normaal
,
de raakvectorruimte, tangentenvectorruimte of raakvlak genoemd. De normaal 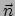 in
in 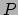 op het oppervlak
op het oppervlak 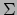 is de eenheidsvector in
is de eenheidsvector in 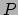 loodrecht op
loodrecht op 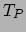 .
Het volgende resultaat was reeds vóór Gauss bekend.
.
Het volgende resultaat was reeds vóór Gauss bekend.
Figuur 60:
Door 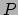 gaat een vlak
gaat een vlak 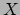 dat normaalvector
dat normaalvector 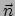 bevat. Het vlak
bevat. Het vlak 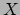 snijdt gebogen oppervlak
snijdt gebogen oppervlak 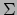 langs curve
langs curve 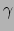 . De eenheidsvector
. De eenheidsvector 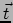 is tangentiaal aan
is tangentiaal aan 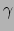 en geeft de richting van deze snede. De vector
en geeft de richting van deze snede. De vector 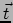 ligt in het tangentenvlak
ligt in het tangentenvlak 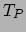 .
.
|
|
Stelling van Euler (1760): Zij 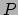 een punt van het oppervlak
een punt van het oppervlak 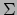 en
zij
en
zij 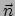 de normaal in
de normaal in 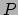 op
op 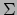 (zie Fig. 60).
Zij
(zie Fig. 60).
Zij 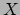 een vlak door
een vlak door 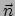 en zij
en zij
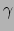 de doorsnijding van
de doorsnijding van 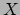 en
en 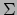 (dit is een kromme) en laat
(dit is een kromme) en laat 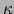 de kromming van
de kromming van 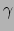 in
in 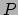 zijn. Dan bestaat er een vlak
zijn. Dan bestaat er een vlak 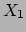 (respectievelijk
(respectievelijk 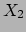 )
door
)
door 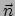 waarvoor
waarvoor
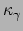 maximaal (respectievelijk minimaal) is en men
noemt deze kromming dan
maximaal (respectievelijk minimaal) is en men
noemt deze kromming dan 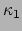 (respectievelijk
(respectievelijk 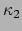 ). Als het vlak
). Als het vlak 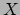 een hoek
een hoek 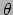 maakt met
maakt met 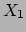 , dan geldt
, dan geldt
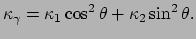 |
(408) |
De krommingen 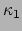 en
en 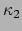 heten de hoofdkrommingen.
Fig. 61 geeft een beeld van de kromming van ruimte
met negatieve kromming (dit lijkt op een zadeloppervlak).
heten de hoofdkrommingen.
Fig. 61 geeft een beeld van de kromming van ruimte
met negatieve kromming (dit lijkt op een zadeloppervlak).
Figuur 61:
Schets van een gebogen oppervlak waarbij de vlakken met hoofdkrommingen
zijn aangegeven, evenals het tangentenvlak.
|
|
De theorie van de gebogen oppervlakken werd aanzienlijk verder ontwikkeld door
C.F. Gauss in zijn artikel `Disquisitiones generales circa superficies curvas' uit
1827. Gauss beschreef hierin een oppervlak met behulp van de parametervoorstelling
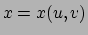 ,
, 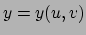 en
en 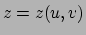 of samengevat
of samengevat
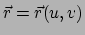 en
zoals Fig. 62 toont
ontstaan hiermee op het oppervlak krommen
en
zoals Fig. 62 toont
ontstaan hiermee op het oppervlak krommen
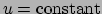 en
en
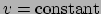 .
We benadrukken dat een punt op het oppervlak
.
We benadrukken dat een punt op het oppervlak 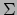 wordt vastgelegd door twee
reële parameters
wordt vastgelegd door twee
reële parameters 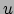 en
en 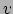 , namelijk
, namelijk
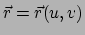 .
.
Figuur 62:
Coördinaten van Gauss voor de beschrijving van een gebogen oppervlak.
|
|
Een kromme
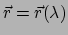 in het oppervlak
in het oppervlak 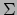 is dus ook te
geven door een parametervoorstelling
is dus ook te
geven door een parametervoorstelling
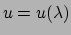 en
en
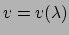 . De
afstand
. De
afstand 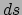 tussen twee infinitesimaal van elkaar verwijderde punten
tussen twee infinitesimaal van elkaar verwijderde punten
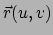 en
en
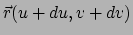 wordt gegeven door
wordt gegeven door
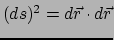 met
met
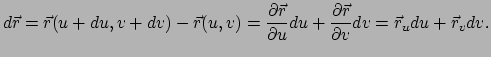 |
(409) |
We vinden hiermee voor de afstand
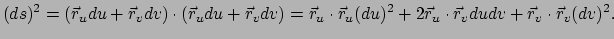 |
(410) |
Met de traditionele afkortingen
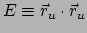 ,
,
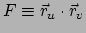 en
en
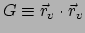 vinden we
vinden we
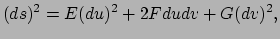 |
(411) |
met 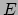 ,
, 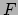 en
en 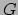 functies van
functies van 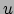 en
en 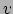 . Deze kwadratische vorm voor
. Deze kwadratische vorm voor 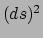 heet de eerste fundamentaalvorm of de metriek. Als het oppervlak
heet de eerste fundamentaalvorm of de metriek. Als het oppervlak  een plat vlak is dan geldt bijvoorbeeld
een plat vlak is dan geldt bijvoorbeeld
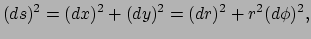 |
(412) |
naar gelang men voor 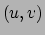 cartesische coördinaten of poolcoördinaten
kiest. Tegenwoordig noteert men voor
cartesische coördinaten of poolcoördinaten
kiest. Tegenwoordig noteert men voor 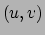 ook wel
ook wel
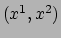 , dus
, dus
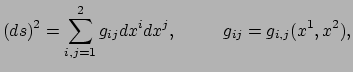 |
(413) |
met
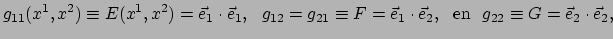 |
(414) |
waarbij
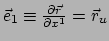 de raakvector
aan de coördinaatlijn
de raakvector
aan de coördinaatlijn
 en
en
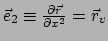 de raakvector
aan de coördinaatlijn
de raakvector
aan de coördinaatlijn
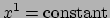 is. Dus
is. Dus
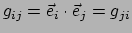 .
De vectoren
.
De vectoren 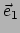 en
en 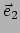 vormen een basis van de twee-dimensionale
raakvectorruimte in
vormen een basis van de twee-dimensionale
raakvectorruimte in
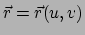 aan
aan  . Iedere raakvector in dit
punt is een lineaire combinatie van
. Iedere raakvector in dit
punt is een lineaire combinatie van 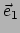 en
en 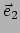 ,
,
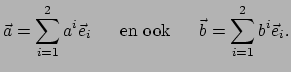 |
(415) |
Voor het inproduct in de raakvectorruimte geldt
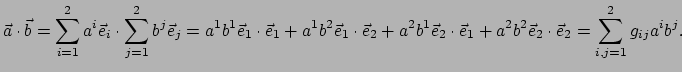 |
(416) |
Zij 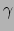 een kromme in het oppervlak
een kromme in het oppervlak 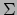 en laat
en laat 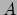 en
en 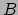 twee punten op
twee punten op
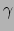 zijn, dan definieert men de booglengte
zijn, dan definieert men de booglengte 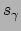 langs
langs 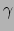 tussen
tussen
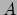 en
en 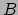 als
als
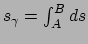 . Als de kromme
. Als de kromme 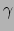 wordt voorgesteld
door
wordt voorgesteld
door
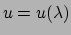 en
en
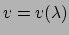 , dan volgt in verband met
, dan volgt in verband met
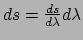 dat
dat
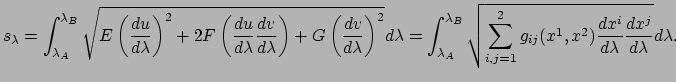 |
(417) |
Laat 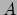 en
en 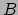 twee punten van het oppervlak
twee punten van het oppervlak 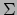 zijn, dan is de geodeet
door
zijn, dan is de geodeet
door 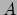 en
en 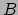 die kromme
die kromme 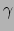 in
in 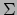 waarvoor de booglengte
waarvoor de booglengte 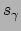 tussen
tussen 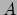 en
en 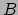 minimaal (of extremaal) is. In het euclidische vlak is een rechte
een geodeet en omgekeerd. Op de bol is een grote cirkel (dit is een cirkel waarvan
het vlak door het middelpunt van de bol gaat) een geodeet en omgekeerd. Merk op
dat de intrinsieke meetkunde van het oppervlak, dat is de meetkunde van
twee-dimensionale wezens die in het oppervlak leven en die geen weet hebben van
de drie-dimensionale ruimte, geheel bepaald wordt door de metriek
minimaal (of extremaal) is. In het euclidische vlak is een rechte
een geodeet en omgekeerd. Op de bol is een grote cirkel (dit is een cirkel waarvan
het vlak door het middelpunt van de bol gaat) een geodeet en omgekeerd. Merk op
dat de intrinsieke meetkunde van het oppervlak, dat is de meetkunde van
twee-dimensionale wezens die in het oppervlak leven en die geen weet hebben van
de drie-dimensionale ruimte, geheel bepaald wordt door de metriek 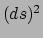 . De
hoofdkrommingen
. De
hoofdkrommingen 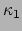 en
en 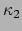 van een punt
van een punt 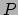 in
in 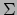 zijn
intrinsieke eigenschappen van het oppervlak. Dit is eenvoudig in te zien aan de hand
van het volgende voorbeeld. Voor een plat vlak (bijvoorbeeld een vel papier)
geldt
zijn
intrinsieke eigenschappen van het oppervlak. Dit is eenvoudig in te zien aan de hand
van het volgende voorbeeld. Voor een plat vlak (bijvoorbeeld een vel papier)
geldt
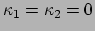 en
en
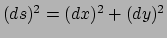 . Als het vel papier
tot een cylinder wordt gevouwen, dan gebeurt er niets met de metriek, maar
. Als het vel papier
tot een cylinder wordt gevouwen, dan gebeurt er niets met de metriek, maar 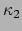 wordt ongelijk aan nul. Het opmerkelijke is nu, dat er een combinatie van
wordt ongelijk aan nul. Het opmerkelijke is nu, dat er een combinatie van 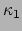 en
en 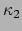 bestaat die ongewijzigd blijft bij het vouwen van het papier. Dit
is de gausskromming.
bestaat die ongewijzigd blijft bij het vouwen van het papier. Dit
is de gausskromming.
Theorema egregium van Gauss: De gausskromming
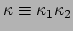 is een intrinsieke grootheid, dit wil zeggen geheel bepaald door de metriek, namelijk
is een intrinsieke grootheid, dit wil zeggen geheel bepaald door de metriek, namelijk
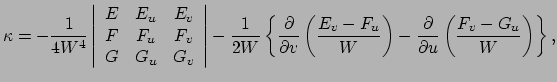 |
(418) |
met
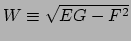 .
.
Merk op dat  slechts afhangt van de metriek via
slechts afhangt van de metriek via  ,
,  en
en 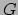 en eerste en
tweede orde afgeleiden hiervan, waardoor
en eerste en
tweede orde afgeleiden hiervan, waardoor 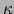 inderdaad een intrinsieke grootheid
is. De hoofdkrommingen hangen bovendien nog af van de wijze waarop het oppervlak
is ingebed in de drie-dimensionale ruimte. De gausskromming is een functie van
inderdaad een intrinsieke grootheid
is. De hoofdkrommingen hangen bovendien nog af van de wijze waarop het oppervlak
is ingebed in de drie-dimensionale ruimte. De gausskromming is een functie van 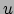 en
en 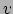 ,
,
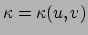 . Oppervlakken van constante kromming zijn oppervlakken waarvoor
. Oppervlakken van constante kromming zijn oppervlakken waarvoor
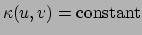 . Hiervan bestaan drie typen, namelijk
. Hiervan bestaan drie typen, namelijk
- het sferische vlak (eenheidsbol) met metriek
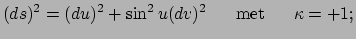 |
(419) |
- het euclidische vlak (in poolcoördinaten) met metriek
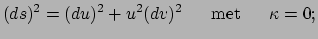 |
(420) |
- het hyperbolische vlak met metriek
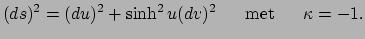 |
(421) |
Het laatste geval is de niet-euclidische meetkunde van Gauss-Lobachevski-Bolyai.
In het volgende beschouwen we een infinitesimaal parallellogram in 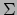 (zie Fig. 63).
(zie Fig. 63).
Figuur 63:
Een infinitesimaal parallellogram in een gebogen oppervlak.
|
|
De zijden
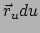 en
en
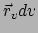 resulteren in een oppervlakte
resulteren in een oppervlakte
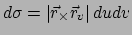 .
Merk op dat
.
Merk op dat
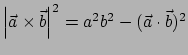 omdat
omdat
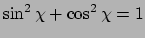 . Dus volgt
. Dus volgt
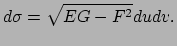 |
(422) |
De stelling uit de euclidische meetkunde die zegt dat de som van de hoeken van
een driehoek 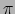 is kan nu worden gegeneraliseerd. Een driehoek in het oppervlak
is kan nu worden gegeneraliseerd. Een driehoek in het oppervlak
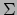 is een drietal punten
is een drietal punten 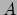 ,
, 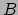 en
en 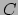 in
in 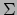 verbonden door de
geodeten tussen puntenparen (zie Fig. 64).
verbonden door de
geodeten tussen puntenparen (zie Fig. 64).
Figuur 64:
Een geodetendriehoek.
|
|
Laat 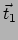 en
en 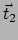 eenheidsraakvectoren in
eenheidsraakvectoren in 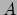 zijn aan de twee geodeten
(de zijden
zijn aan de twee geodeten
(de zijden 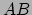 en
en 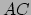 van de geodetendriehoek) door
van de geodetendriehoek) door 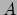 , dan is de hoek
, dan is de hoek 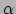 gedefinieerd met behulp van
gedefinieerd met behulp van
 |
(423) |
Voor  en
en  analoog. Dan geldt
analoog. Dan geldt
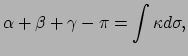 |
(424) |
waarbij de integraal over het oppervlak van de geodetendriehoek wordt
uitgevoerd en 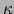 de gausskromming is. In het bijzondere geval van een oppervlak met
constante kromming geldt
de gausskromming is. In het bijzondere geval van een oppervlak met
constante kromming geldt
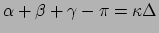 ,
waarin
,
waarin 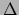 het oppervlak van de driehoek is; voor
het oppervlak van de driehoek is; voor
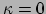 wordt
inderdaad het resultaat uit de euclidische meetkunde teruggevonden.
wordt
inderdaad het resultaat uit de euclidische meetkunde teruggevonden.




Next: Riemannse meetkunde
Up: Appendix - Meetkunde
Previous: Appendix - Meetkunde
Contents
Jo van den Brand
2009-01-31
![\includegraphics[width=8cm]{Figures/curve.eps}](img1674.png)
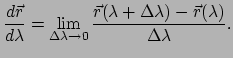
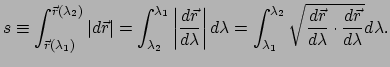
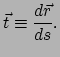
![\includegraphics[width=5cm]{Figures/frenet.eps}](img1701.png)
![]() ) volgt
) volgt
![]() . Differentiatie naar
. Differentiatie naar ![]() geeft, met vergelijkingen (
geeft, met vergelijkingen (
![]() ) en (
) en (
![]() )
)
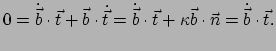
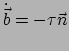 , waarbij
, waarbij 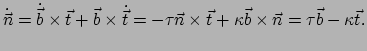
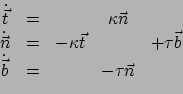
![\includegraphics[width=8cm]{Figures/plane.eps}](img1718.png)
![]() . In de tijd voor Gauss
werd een gebogen oppervlak voorgesteld door
. In de tijd voor Gauss
werd een gebogen oppervlak voorgesteld door
![]() of
of
![]() . In het
bijzonder kan men krommen in een dergelijk oppervlak beschouwen en voor deze
krommen kan men uiteraard de bovenstaande begrippen invoeren.
Fig. 59 toont dat
. In het
bijzonder kan men krommen in een dergelijk oppervlak beschouwen en voor deze
krommen kan men uiteraard de bovenstaande begrippen invoeren.
Fig. 59 toont dat ![]() een
kromme in het oppervlak
een
kromme in het oppervlak ![]() is met
is met ![]() een punt op
een punt op ![]() . Dan heeft
. Dan heeft ![]() een raakvector
een raakvector
![]() in het punt
in het punt ![]() . Beschouw nu alle mogelijke
krommen in
. Beschouw nu alle mogelijke
krommen in ![]() door
door ![]() , dan vormt de verzameling van alle bijbehorende
raakvectoren
, dan vormt de verzameling van alle bijbehorende
raakvectoren
![]() een twee-dimensionale vectorruimte
een twee-dimensionale vectorruimte ![]() ,
de raakvectorruimte, tangentenvectorruimte of raakvlak genoemd. De normaal
,
de raakvectorruimte, tangentenvectorruimte of raakvlak genoemd. De normaal ![]() in
in ![]() op het oppervlak
op het oppervlak ![]() is de eenheidsvector in
is de eenheidsvector in ![]() loodrecht op
loodrecht op ![]() .
Het volgende resultaat was reeds vóór Gauss bekend.
.
Het volgende resultaat was reeds vóór Gauss bekend.
![\includegraphics[width=10cm]{Figures/euler1.eps}](img1723.png)
![]() een punt van het oppervlak
een punt van het oppervlak ![]() en
zij
en
zij ![]() de normaal in
de normaal in ![]() op
op ![]() (zie Fig. 60).
Zij
(zie Fig. 60).
Zij ![]() een vlak door
een vlak door ![]() en zij
en zij
![]() de doorsnijding van
de doorsnijding van ![]() en
en ![]() (dit is een kromme) en laat
(dit is een kromme) en laat ![]() de kromming van
de kromming van ![]() in
in ![]() zijn. Dan bestaat er een vlak
zijn. Dan bestaat er een vlak ![]() (respectievelijk
(respectievelijk ![]() )
door
)
door ![]() waarvoor
waarvoor
![]() maximaal (respectievelijk minimaal) is en men
noemt deze kromming dan
maximaal (respectievelijk minimaal) is en men
noemt deze kromming dan ![]() (respectievelijk
(respectievelijk ![]() ). Als het vlak
). Als het vlak ![]() een hoek
een hoek ![]() maakt met
maakt met ![]() , dan geldt
, dan geldt
![\includegraphics[width=10cm]{Figures/zadel.eps}](img1730.png)
![]() ,
, ![]() en
en ![]() of samengevat
of samengevat
![]() en
zoals Fig. 62 toont
ontstaan hiermee op het oppervlak krommen
en
zoals Fig. 62 toont
ontstaan hiermee op het oppervlak krommen
![]() en
en
![]() .
We benadrukken dat een punt op het oppervlak
.
We benadrukken dat een punt op het oppervlak ![]() wordt vastgelegd door twee
reële parameters
wordt vastgelegd door twee
reële parameters ![]() en
en ![]() , namelijk
, namelijk
![]() .
.
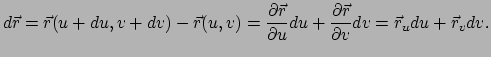
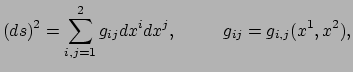
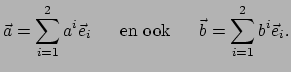
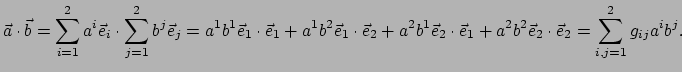
![]() een kromme in het oppervlak
een kromme in het oppervlak ![]() en laat
en laat ![]() en
en ![]() twee punten op
twee punten op
![]() zijn, dan definieert men de booglengte
zijn, dan definieert men de booglengte ![]() langs
langs ![]() tussen
tussen
![]() en
en ![]() als
als
![]() . Als de kromme
. Als de kromme ![]() wordt voorgesteld
door
wordt voorgesteld
door
![]() en
en
![]() , dan volgt in verband met
, dan volgt in verband met
![]() dat
dat
![]() is een intrinsieke grootheid, dit wil zeggen geheel bepaald door de metriek, namelijk
is een intrinsieke grootheid, dit wil zeggen geheel bepaald door de metriek, namelijk
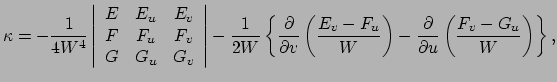
![]() slechts afhangt van de metriek via
slechts afhangt van de metriek via ![]() ,
, ![]() en
en ![]() en eerste en
tweede orde afgeleiden hiervan, waardoor
en eerste en
tweede orde afgeleiden hiervan, waardoor ![]() inderdaad een intrinsieke grootheid
is. De hoofdkrommingen hangen bovendien nog af van de wijze waarop het oppervlak
is ingebed in de drie-dimensionale ruimte. De gausskromming is een functie van
inderdaad een intrinsieke grootheid
is. De hoofdkrommingen hangen bovendien nog af van de wijze waarop het oppervlak
is ingebed in de drie-dimensionale ruimte. De gausskromming is een functie van ![]() en
en ![]() ,
,
![]() . Oppervlakken van constante kromming zijn oppervlakken waarvoor
. Oppervlakken van constante kromming zijn oppervlakken waarvoor
![]() . Hiervan bestaan drie typen, namelijk
. Hiervan bestaan drie typen, namelijk
![]() (zie Fig. 63).
(zie Fig. 63).
 omdat
omdat