This blog post was originally posted on the homepage of the XENON1T collaboration.
—————————————
Since the first release of dark matter search results based on the 1 tonne-year exposure of the XENON1T experiment, the collaboration has published more WIMP signal searches based on the same dataset. Those articles are usually written in a brief way and are focusing on the communication of the scientific results.
In order to give more details on the XENON1T dark matter analysis, we have previously published a paper focusing on the signal and background models and the statistical inference using this data. It has been complemented by a new article that reveals details on the challenges of detector characterization and data preparation before it is ready to be used for model building and statistical inference in order to make statements on dark matter.
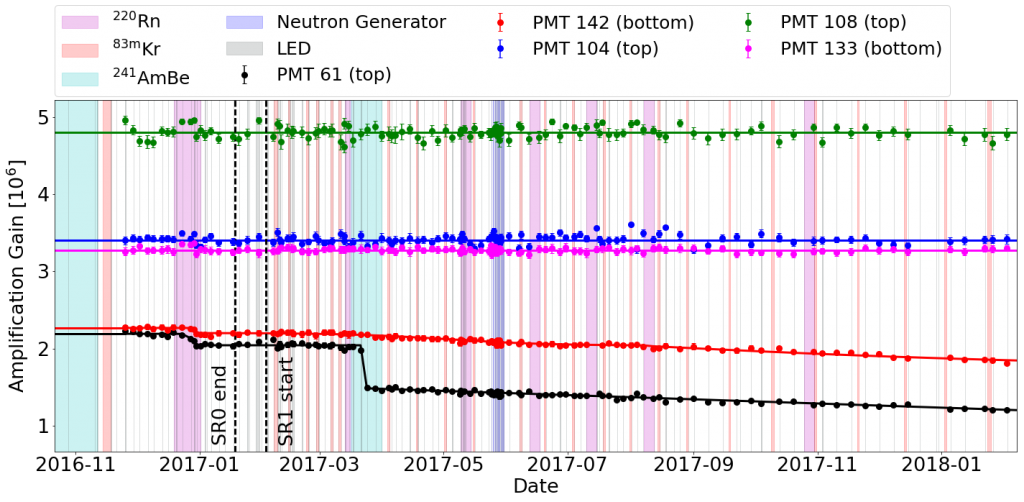
The XENON1T experiment performed two science runs between October 2016 and February 2018, reaching a total data livetime of 279 days. During that time the detector had to be operated in a very stable mode in order to ensure undistorted signals. If some conditions change over time they have to be modeled over time in order to account for them in the take them into account during data analysis and include them into the models. One example for those changes are the ones at the photosensors. Each sensor has an individual amplification factor, i.e. gain, that is a function of the applied high voltage. few sensors developed malfunctions during the science runs because of which the amplification factor decreased over time or the voltage had to be reduced resulting in a sudden decreased of the amplification. Those variations are shown in red and black for two sensors as a function of time in the following figure while green, blue and magenta show stable sensors which are representative for the majority of the XENON1T light detectors.
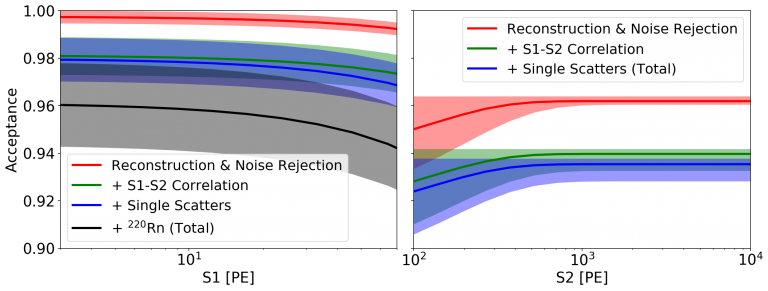
As soon as the detector operation conditions are modeled the data is put through selection criteria that reduce the number of background-like signatures and therefore enhance the signal to background ratio. The criteria are grouped into four general types:
Modelling how an electronic or nuclear recoil will look like in the detector is crucial both to know the shape of a WIMP signal, and to model the backgrounds well. XENON1T uses a comprehensive fit to multiple calibration sources to constrain the distributions of backgrounds and signals in the analysis space; S1, S2 and the radius from the center axis of the detector. Some background components are harder to model directly, and are estimated by using sidebands or other data samples. In the XENON1T analysis, coincidences between unrelated, lone S1 and S2 events were modeled this way, in addition to the surface background– events occurring close to or at the detector wall.
The models of each background and the signal, for two separate science runs, are put together in a likelihood, which is a mathematical function of the WIMP signal strength as well as nuisance parameters. These are unknowns that could change the analysis, such as the true expectation value for each background component. The likelihood also contains multiple terms representing measurements of nuisance parameter, which constrain them when the likelihood is fitted to the data collected by XENON1T. The value of the likelihood evaluated at a specific signal strength has a random distribution which is estimated using simulated realizations of the experimental outcome. The final statistical limits are computed by comparing the likelihood computed on the actual data with the distributions found from the simulations.
