- ... aangetoond1
- Of die slechts in experimenten voorkwamen,
die niet door andere experimentatoren herhaald konden worden!
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
hebben2
- Het zal duidelijk zijn dat niet alle theoretici
`enthousiast zijn' over deze gepostuleerde deeltjes. Verder is het
onduidelijk of het mogelijk is met tachyonen een signaal (informatie)
over te brengen - iets dat in conflict zou zijn met de
speciale relativiteitstheorie.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... belang3
- en soms ook het magnetische
moment, bijvoorbeeld in de hyperfijnwisselwerking.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... Tegenwoordig4
- We verwaarlozen
hier subtiliteiten als bijvoorbeeld de virtuele mesonen in het
binnenste van de kern.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... antineutrino5
- Een
eenvoudige quantummechanische berekening laat zien, dat er teveel
energie voor nodig is om een elektron te binden binnen het volume
van een kern.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... worden6
- De quantumgetallen karakteriseren
een bepaalde toestand van een systeem van deeltjes. Ze zijn constant
(men zegt behouden) zolang het systeem ongestoord is.
Quantumgetallen hebben te maken met behoudswetten. Een
voorbeeld is de wet van behoud van lading. Een uitzondering hierbij is de
spin, want enkel het totale impulsmoment is behouden: spin en
baanimpulsmoment. Verder zijn sommige behoudswetten niet altijd
strikt geldig: zoals de wet van behoud van vreemdheid.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... uitgevoerd7
- Hij ontving hiervoor in 1936
de Nobelprijs voor de natuurkunde; hij was toen 31 jaar oud. Een
jaar later ontdekte hij het muon.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... leptonen8
- Oorspronkelijk werden de deeltjes
ingedeeld aan de hand van de massa: de lichte deeltjes ofwel leptonen
(
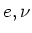 ) met
) met 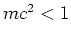 MeV, de middelzware deeltjes ofwel mesonen
met
MeV, de middelzware deeltjes ofwel mesonen
met
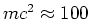 MeV en de zware deeltjes ofwel baryonen met
MeV en de zware deeltjes ofwel baryonen met
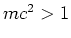 GeV. Deze klassificatie is echter niet zinvol: de muonen
(
GeV. Deze klassificatie is echter niet zinvol: de muonen
(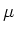 ) en de tau's (
) en de tau's (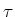 ) gedragen zich analoog aan het elektron, ondanks
dat ze een geheel verschillende massa hebben.
) gedragen zich analoog aan het elektron, ondanks
dat ze een geheel verschillende massa hebben.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
behoudswetten9
- We kunnen dit ook
anders formuleren: indien de lading
(of bijvoorbeeld het baryongetal) strikt behouden
is, dan kan het lichtste geladen deeltje,
het elektron (of bijvoorbeeld het lichtste
baryon, het proton) niet vervallen.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
down-quarks10
- We verwaarlozen voorlopig het
feit, dat in het nucleon ook een (omstreden)
hoeveelheid
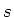 ,
, 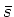 en andere
quarks bijgemengd zijn. Ook worden de drie `kleuren' van de quarks pas later
besproken.
en andere
quarks bijgemengd zijn. Ook worden de drie `kleuren' van de quarks pas later
besproken.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
wisselwerking11
- Gedurende de laatste jaren was er regelmatig
sprake van een zogenaamde vijfde kracht, die als een modificatie van
de gravitatiepotentiaal ingevoerd werd:
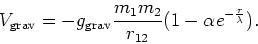 |
(7) |
Een heranalyse door Fischbach (1986) van de oude data van Eötvos
resulteerde aanvankelijk in
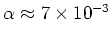 en
en
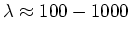 m. Fischbach's publicatie gaf aanleiding
tot een serie nieuwe experimenten (waaronder zeer geraffineerde
metingen met torsieslingers), die aanvankelijk ook aanwijzingen gaven
voor het bestaan van zo'n vijfde kracht met een middellange
reikwijdte. Op dit moment (1998) is men bezig met
een nieuwe reeks zorgvuldige experimenten en de voorlopige resultaten
duiden erop dat de effecten te verklaren zijn, zonder dat een additionele
wisselwerking ingevoerd dient te worden.
m. Fischbach's publicatie gaf aanleiding
tot een serie nieuwe experimenten (waaronder zeer geraffineerde
metingen met torsieslingers), die aanvankelijk ook aanwijzingen gaven
voor het bestaan van zo'n vijfde kracht met een middellange
reikwijdte. Op dit moment (1998) is men bezig met
een nieuwe reeks zorgvuldige experimenten en de voorlopige resultaten
duiden erop dat de effecten te verklaren zijn, zonder dat een additionele
wisselwerking ingevoerd dient te worden.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... kernkracht12
- Teneinde verwarring te voorkomen zullen we
in het vervolg spreken over de kernkracht, als we de wisselwerking
van baryonen en mesonen bedoelen en daarbij hun inwendige structuur, welke
bij lage energieën niet van belang is, verwaarlozen. Daarentegen bedoelen
we met de sterke wisselwerking die krachten, die tussen de quarks
werkzaam zijn.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... gekarakteriseerd13
- De
zwakke wisselwerking schendt bijvoorbeeld, zoals we later nog
uitvoerig zullen bespreken, de pariteit ofwel spiegelsymmetrie.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... ook14
- Na enkele
dwalingen, want aanvankelijk werden in 1937 muonen ontdekt door
Carl Anderson en Neddermayer in experimenten met kosmische
straling. Muonen hebben echter totaal niets te maken met de
sterke wisselwerking.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
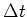 15
15
- Omdat
de energie op tijd teruggegeven dient te worden, de wet
van behoud van energie is immers geschonden, noemt men zo'n deeltje
een virtueel deeltje. Het kan niet worden waargenomen.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
gravitatie16
- Uiteraard hebben we het nu niet over
de complicaties die voortvloeien uit de algemene
relativiteitstheorie.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
worden17
- We zullen later dieper ingaan op al deze
eigenschappen van de kernkracht.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... bosonen18
- Wolfgang Pauli,
Physical Review 58 (1940) 716.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... verstrooiingstheorie19
- Het zal duidelijk zijn dat voor
een volledige discussie relativistische kinematica, quantum mechanica,
en in het algemene geval, van creatie en annihililatie van deeltjes,
ook quantumveldentheorie vereist is.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
algemeen20
- Een uitzondering vormen de experimenten met neutronen,
die vaak door een kernreactor kunnen worden geproduceerd.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... reactie21
- Hoe groter de
oppervlakte van het target deeltje, des te gemakkelijker kunnen we
het raken; het bundeldeeltje zal dientengevolge worden verstrooid.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
som22
- In enkele gevallen, namelijk indien de verschillende
eindkanalen niet onderscheidbaar zijn, moeten niet de
werkzame doorsneden, maar de amplituden voor de verschillende processen
opgeteld worden (zogenaamde coherente processen).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... plaats23
- In de literatuur vindt
men vaak, meestal als het gaat om materiaaleigenschappen
en de berekening van afscherming, niet de werkzame doorsnede
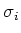 getabelleerd, maar de macroscopische (partiële) werkzame
doorsnede
getabelleerd, maar de macroscopische (partiële) werkzame
doorsnede
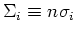 [ m
[ m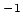 ], de
verzwakkingcoëfficient
], de
verzwakkingcoëfficient
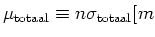 ^-1
^-1
![$ ], en de {\sl massaverzwakkingsco\uml efficient}
$](img301.gif) _ totaal N_A A _ totaal
_ totaal N_A A _ totaal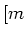 ^2
^2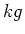 ^-1
^-1![$ ]. Hierbij is $](img304.gif) N_A = 6.022 136 7(36) 10^23
N_A = 6.022 136 7(36) 10^23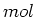 ^-1
^-1
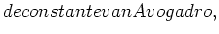 A
A
![$ [ kg/kmol ] het atoomgewicht
van het target, en $](img307.gif)
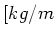 ^3
^3
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... energie24
- Van belang is natuurlijk in alle gevallen de
Galileï-, of de Lorentzinvariante relatieve energie van de
reactiepartners. In het niet-relativistische geval zullen we rekenen
met
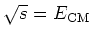 , terwijl
we relativistisch,
, terwijl
we relativistisch,
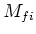 , de totale energie in het
zwaartepunt zullen gebruiken. Later zullen we het relativistische
correcte verband bespreken tussen het matrixelement
, de totale energie in het
zwaartepunt zullen gebruiken. Later zullen we het relativistische
correcte verband bespreken tussen het matrixelement 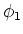 ,
het faseruimte volume, en de werkzame doorsnede, alsook de transformatie
van de reactiewaarschijnlijkheden in verschillende systemen.
,
het faseruimte volume, en de werkzame doorsnede, alsook de transformatie
van de reactiewaarschijnlijkheden in verschillende systemen.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... volgt25
- Een uitvoerige afleiding kan
gevonden worden in bijvoorbeeld M.L. Goldberger and K.M. Watson,
Collision Theory, J. Wiley, New York, 1967 (p. 58 ff.). Laat je
niet afleiden door het feit dat in veel boeken andere machten van
(
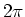 ) gebruikt worden. Het staat iedere auteur vrij om de normering
van de golffuncties te kiezen zoals hij/zij belieft. Merk verder op,
dat in veel theoretische werken vaak
) gebruikt worden. Het staat iedere auteur vrij om de normering
van de golffuncties te kiezen zoals hij/zij belieft. Merk verder op,
dat in veel theoretische werken vaak 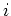 gebruikt wordt.
gebruikt wordt.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... geldt26
- We
hebben een dergelijke uitdrukking reeds eerder gebruikt bij de berekening van
overgangswaarschijnlijkheden voor deeltjesverval.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... integratie27
- We gebruiken hier
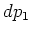 .
Deze relatie is ook relativistisch correct.
.
Deze relatie is ook relativistisch correct.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... is28
- Als de
deeltjes spin bezitten dient deze uitdrukking gemodificeerd
te worden met statistische spinfactoren.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... is29
- Wat zeker niet
altijd geldig is! Enkele belangrijke uitzonderingen zullen we nog
bespreken.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
hebben30
- Het matrixelement bevat
twee termen,
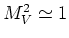 .
Indien
.
Indien
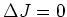 , dan hebben we te maken met een
zogenaamde Fermi overgang, waarbij de spin niet veranderd
(
, dan hebben we te maken met een
zogenaamde Fermi overgang, waarbij de spin niet veranderd
(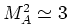 ). Indien
). Indien
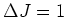 , dan spreken we van
een Gamow-Teller overgang (
, dan spreken we van
een Gamow-Teller overgang (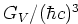 ), waarbij er drie
spin instellingen mogelijk zijn. In neutronverval dragen beide
termen bij. De koppelingskonstanten zijn
), waarbij er drie
spin instellingen mogelijk zijn. In neutronverval dragen beide
termen bij. De koppelingskonstanten zijn
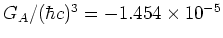 GeV
GeV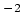 en
en
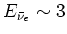 GeV
GeV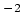 (dit alles zonder bewijs; zie bijvoorbeeld
R.R. Roy and B.P. Nigam, Nuclear Physics, J. Wiley, New York 1967,
waar de hele spinalgebra behandeld wordt).
(dit alles zonder bewijs; zie bijvoorbeeld
R.R. Roy and B.P. Nigam, Nuclear Physics, J. Wiley, New York 1967,
waar de hele spinalgebra behandeld wordt).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... verstrooiingstheorie31
- Het zal duidelijk zijn dat voor
een volledige discussie relativistische kinematica, quantum mechanica,
en in het algemene geval, van creatie en annihililatie van deeltjes,
ook quantumveldentheorie vereist is.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
algemeen32
- Een uitzondering vormen de experimenten met neutronen,
die vaak door een kernreactor kunnen worden geproduceerd.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... reactie33
- Hoe groter de
oppervlakte van het target deeltje, des te gemakkelijker kunnen we
het raken; het bundeldeeltje zal dientengevolge worden verstrooid.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
som34
- In enkele gevallen, namelijk indien de verschillende
eindkanalen niet onderscheidbaar zijn, moeten niet de
werkzame doorsneden, maar de amplituden voor de verschillende processen
opgeteld worden (zogenaamde coherente processen).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... plaats35
- In de literatuur vindt
men vaak, meestal als het gaat om materiaaleigenschappen
en de berekening van afscherming, niet de werkzame doorsnede $_i
_i n_i
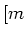 ^-1
_ totaal n_ totaal
[ m
^-1
_ totaal n_ totaal
[ m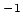 ], en de massaverzwakkingscoëfficient
[ m
], en de massaverzwakkingscoëfficient
[ m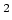 kg
kg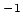 ]. Hierbij is
mol
]. Hierbij is
mol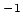 de constante van Avogadro,
de constante van Avogadro, 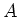 [ kg/kmol ] het atoomgewicht
van het target, en
[ kg/kmol ] het atoomgewicht
van het target, en 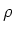 [ kg/m
[ kg/m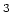 ] de dichtheid van het target.
] de dichtheid van het target.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... energie36
- Van belang is natuurlijk in alle gevallen de
Galileï-, of de Lorentzinvariante relatieve energie van de
reactiepartners. In het niet-relativistische geval zullen we rekenen
met
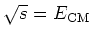 , terwijl
we relativistisch,
, terwijl
we relativistisch,
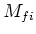 , de totale energie in het
zwaartepunt zullen gebruiken. Later zullen we het relativistische
correcte verband bespreken tussen het matrixelement
, de totale energie in het
zwaartepunt zullen gebruiken. Later zullen we het relativistische
correcte verband bespreken tussen het matrixelement 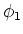 ,
het faseruimte volume, en de werkzame doorsnede, alsook de transformatie
van de reactiewaarschijnlijkheden in verschillende systemen.
,
het faseruimte volume, en de werkzame doorsnede, alsook de transformatie
van de reactiewaarschijnlijkheden in verschillende systemen.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... volgt37
- Een uitvoerige afleiding kan
gevonden worden in bijvoorbeeld M.L. Goldberger and K.M. Watson,
Collision Theory, J. Wiley, New York, 1967 (p. 58 ff.). Laat je
niet afleiden door het feit dat in veel boeken andere machten van
(
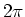 ) gebruikt worden. Het staat iedere auteur vrij om de normering
van de golffuncties te kiezen zoals hij/zij belieft. Merk verder op,
dat in veel theoretische werken vaak
) gebruikt worden. Het staat iedere auteur vrij om de normering
van de golffuncties te kiezen zoals hij/zij belieft. Merk verder op,
dat in veel theoretische werken vaak 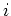 gebruikt wordt.
gebruikt wordt.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... geldt38
- We
hebben een dergelijke uitdrukking reeds eerder gebruikt bij de berekening van
overgangswaarschijnlijkheden voor deeltjesverval.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... integratie39
- We gebruiken hier
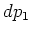 .
Deze relatie is ook relativistisch correct.
.
Deze relatie is ook relativistisch correct.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... is40
- Als de
deeltjes spin bezitten dient deze uitdrukking gemodificeerd
te worden met statistische spinfactoren.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... is41
- Wat zeker niet
altijd geldig is! Enkele belangrijke uitzonderingen zullen we nog
bespreken.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
hebben42
- Het matrixelement bevat
twee termen,
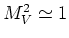 .
Indien
.
Indien
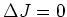 , dan hebben we te maken met een
zogenaamde Fermi overgang, waarbij de spin niet veranderd
(
, dan hebben we te maken met een
zogenaamde Fermi overgang, waarbij de spin niet veranderd
(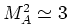 ). Indien
). Indien
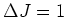 , dan spreken we van
een Gamow-Teller overgang (
, dan spreken we van
een Gamow-Teller overgang (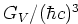 ), waarbij er drie
spin instellingen mogelijk zijn. In neutronverval dragen beide
termen bij. De koppelingskonstanten zijn
), waarbij er drie
spin instellingen mogelijk zijn. In neutronverval dragen beide
termen bij. De koppelingskonstanten zijn
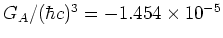 GeV
GeV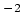 en
en
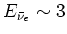 GeV
GeV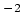 (dit alles zonder bewijs; zie bijvoorbeeld
R.R. Roy and B.P. Nigam, Nuclear Physics, J. Wiley, New York 1967,
waar de hele spinalgebra behandeld wordt).
(dit alles zonder bewijs; zie bijvoorbeeld
R.R. Roy and B.P. Nigam, Nuclear Physics, J. Wiley, New York 1967,
waar de hele spinalgebra behandeld wordt).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
benadering43
- De benadering is goed voor enkele (dus niet
overlappende) nauwe resonanties, die niet sterk met het niet-resonante
deel van de reactie interfereren.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... enkele44
- De ontwerper van een reactor dient dit
echter zeker te doen! De Dopplerverbreding van bepaalde resonanties
(de verbreding door de thermische beweging van de kernen) draagt
wezenlijk bij tot de inherente stabiliteit van een reactor. Verder
is de vraagstelling hoe resonanties statistisch verdeeld zijn
een interessante.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... inzichten45
- Bijvoorbeeld de
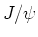 , en de ijkbosonen
en
, en de ijkbosonen
en 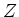 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... deeltjes46
- Aangezien er
tegenwoordig deeltjesversnellers
ter beschikking staan, die deeltjes kunnen produceren
met energieën van vele GeV, zou men deze experimenten nu niet
meer als `hoge-energie fysica' karakteriseren. De grenzen
van de lage-energie kernfysica, medium-energie, en hoge-energie fysica
verschuiven in de tijd.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... is47
- Het is verbazend dat de uitdrukking van
de formule van Rutherford, zoals afgeleid uit de klassieke mechanica,
ook geldig blijft voor een quantummechanische beschrijving.
Dat is echter enkel het geval omdat
. Voor alle andere wisselwerkingen levert de
quantummechanische berekening een ander resultaat op dan de klassieke.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... bepalen48
- Tegenwoordig weten we, dat
de beide botsingspartners naast de ladingswisselwerking ook nog een
sterke wisselwerking hebben. Omdat deze slechts een zeer korte
dracht heeft (
fm), kunnen we stellen dat
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... direct49
- Jammer genoeg volgt uit hetzelfde
argument, dat de benodigde deeltjesversnellers des te groter (en dus
duurder) worden, als we dieper in het inwendige van deeltjes willen
kijken.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... benadering50
- De voorwaarden waaronder
de Bornse benadering geldig is, worden in het college quantummechanica
besproken. Een uitvoerig onderzoek werd uitgevoerd door
R. Jost en A. Pais, Phys. Rev. 82 (1951) 840. Een makkelijk
te begrijpen voorstelling wordt gegeven door R.J. Taylor,
Scattering Theory, J. Wiley, New York (1972). De factor
hangt af van de normering van de golffuncties en
is niet eenduidig in de literatuur.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... spleet51
- Voor de verstrooiing
aan de scherpe randen van een homogene bol met straal vinden
we een minimum voor
.
De positie van het minimum geeft informatie over de ladingstraal.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... raden52
- De afleidingen
zijn te vinden in het boek ` Quarks and Leptons - An Introductory
Course in Modern Particle Physics' van F. Halzen en A.D. Martin.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... vormfactoren53
- Behalve
voor de ladingsvormfactor van het neutron.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... targets54
- De subatomaire
fysica groep van de Vrije Universiteit, Amsterdam speelt een leidende rol
in dit type experimenten. Behalve aan het neutron wordt er ook gewerkt aan
de meting van de vormfactor van het pion.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... doorsnede55
- De geïnteresseerde student
kan de afleiding weer vinden in
in het boek ` Quarks and Leptons - An Introductory
Course in Modern Particle Physics' van F. Halzen en A.D. Martin.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
interactie56
- We hebben reeds
gezien dat de term met
te maken heeft met
het magnetische moment.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
lichtsnelheid57
- De meter is de lengte van het pad dat afgelegd
wordt door licht
in vacuum gedurende een tijdinterval van 1/299 792 458 seconde. Met deze
definitie is de waarde van
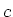 exact.
exact.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... Lorentztransformatie58
- Hierbij is de
Einsteinconventie gebruikt, hetgeen impliceert dat er gesommeerd
wordt over herhaalde indices.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
gedefinieerd59
- De metriek is een wiskundige beschrijving
van de manier waarop afstanden in een ruimte worden gemeten. Men kan
zich dit eenvoudig voorstellen als een matrix . De afstand tussen twee
punten die beschreven worden door de vectoren en
is dan (een matrix vermenigvuldiging). Het eenvoudigste
voorbeeld is de normale drie-dimensionale ruimte, waarvoor
en
. De lengte van de vector
wordt gegeven door .
In deze appendix geven we de definitie van de metrische
tensor zoals we die in de Speciale Relativiteitstheorie gebruiken.
Merk op dat in de Algemene Relativiteitstheorie de metrische tensor
bepaald wordt door de veldvergelijking
waarbij de energie-impuls tensor is, en de
Einstein tensor die de kromming van de ruimte beschrijft. De Einstein tensor
is opgebouwd uit contracties van de krommingstensor, die
een functie is van de metrische tensor en de eerste-
en tweede-orde afgeleiden. De veldvergelijking is dus een differentiaal
vergelijking voor de metriek .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.