| (5) |
Laten we beginnen met een beschouwing uit de klassieke mechanica. De gravitatiewet geeft de kracht tussen twee (voorlopig als puntvormig aangenomen) massa's als
| (5) |
Uit deze krachtwet en de wetten van Newton kon bijvoorbeeld de beweging
van alle planeten in ons zonnestelsel met fantastische nauwkeurigheid
worden afgeleid. Schijnbare afwijkingen bleken later te leiden tot de
grootste triomfen van het model. Zo ontdekte men in het begin van de
negentiende eeuw
dat de planeet Uranus niet voldeed aan de gravitatiewet en bovendien
de behoudswetten voor energie en impulsmoment schond. De oplossing
van deze discrepantie werd in 1846 door U. Le Verrier en John Adams gegeven:
de baan van Uranus wordt door de aantrekkingskracht van een onbekende
planeet beinvloed! Uit de zeer kleine storingen van de baan van Uranus
kon zelfs de plaats van het onbekende object berekend worden. Daadwerkelijk
vond op 23 September 1846 de sterrenkundige Johann
Galle, zoals men zegt: in minder dan een half uur,
binnen 1![]() van de voorspelde positie, de nieuwe planeet Neptunus. Dat
was zonder twijfel één van de grootste successen van de klassieke mechanica.
In het begin van de twintigste eeuw resteerde er in principe slechts
één enkel niet begrepen effect: de periheliumverschuiving van de
planeet die zich het dichtst bij de zon bevindt, namelijk Mercurius. Deze
afwijking (slechts
van de voorspelde positie, de nieuwe planeet Neptunus. Dat
was zonder twijfel één van de grootste successen van de klassieke mechanica.
In het begin van de twintigste eeuw resteerde er in principe slechts
één enkel niet begrepen effect: de periheliumverschuiving van de
planeet die zich het dichtst bij de zon bevindt, namelijk Mercurius. Deze
afwijking (slechts
![]() boogseconde per eeuw) kon enkel
door de algemene relativiteitstheorie van Einstein verklaard worden
(de berekende afwijking bedraagt
boogseconde per eeuw) kon enkel
door de algemene relativiteitstheorie van Einstein verklaard worden
(de berekende afwijking bedraagt ![]() boogseconde per eeuw).
boogseconde per eeuw).
Een vergelijkbare doorbraak deed zich voor in de atoomfysica, nadat de
basiswetten voor de golfmechanica (de Schrödinger en
Diracvergelijking, alsook het Pauli principe) ontdekt waren. Samen met
de wet van Coulomb (beter: de Maxwellvergelijkingen),
| (6) |
Vanzelfsprekend wilde men, aangemoedigd door deze successen, ook in andere gebieden van de natuurkunde een vergelijkbare nauwkeurigheid bereiken. Eerst bij de berekening van kernen en de constituenten ervan (protonen en neutronen) en in een volgende stap, bij de synthese van het nucleon uit zijn basiselementen, de quarks. Deze wens is tot nu toe niet in vervulling gegaan, en in het verloop van dit college zullen we de redenen voor dat falen dienen na te gaan.
In dit hoofdstuk proberen we een overzicht van alle in de natuur
voorkomende krachten te geven. We zijn, door onze ervaring
met de klassieke mechanica en elektrodynamica,
gewend aan het idee dat krachten worden
overgebracht van één lichaam op het andere, door een veld.
Het begrip veld is slechts een hypothese - het veld is fictief,
de kracht daarentegen is aantoonbaar. In de deeltjesfysica is het
bijzonder nuttig om een ander concept in te voeren: het
idee van deeltjesuitwisseling. Dit behelst dat
bepaalde deeltjes ervoor zorgen dat bepaalde krachten worden overgedragen.
Naast de zwaartekracht en de elektromagnetische wisselwerking zullen
we - misschien verbazingwekkend - slechts twee nieuwe krachten hoeven
in te voeren, namelijk de sterke wisselwerking en de zwakke
wisselwerking11.
Nadat men wist dat een kern is samengesteld uit protonen en neutronen, drong zich de vraag op, waarom een kern, ondanks de geweldige elektrische afstoting tussen de positief geladen protonen, gebonden is. Klaarblijkelijk bestaat er een, voorlopig voor ons nog onbekende, wisselwerking die sterker is dan de elektromagnetische, en die men daarom de sterke wisselwerking of de kernkracht12 noemt.
Uit het ![]() -verval van bepaalde kernen (bijvoorbeeld
-verval van bepaalde kernen (bijvoorbeeld
![]() H
H ![]()
![]() He + e
He + e![]() +
+ ![]() ) en later ook uit
het verval van deeltjes (bijvoorbeeld
) en later ook uit
het verval van deeltjes (bijvoorbeeld
![]() e
e
![]() ) kon het bestaan van nog een vierde kracht,
de zogenaamde zwakke wisselwerking afgeleid worden. Deze kracht
wordt door geheel andere eigenschappen gekarakteriseerd13. In de
onderstaande tabel 4 worden enkele van de belangrijkste
eigenschappen van de krachten vermeld.
) kon het bestaan van nog een vierde kracht,
de zogenaamde zwakke wisselwerking afgeleid worden. Deze kracht
wordt door geheel andere eigenschappen gekarakteriseerd13. In de
onderstaande tabel 4 worden enkele van de belangrijkste
eigenschappen van de krachten vermeld.
| Wisselwerking | Sterkte | Dracht | Boson | Massa | Koppelt aan |
| [ e ] | [ GeV/c |
||||
| El. magn | 1/137 | 0 | Lading | ||
| Zwakke |
|
W |
80, 91 | Quarks, Lept. | |
| Gravitatie |
|
Graviton | 0 | Massa | |
| Kernkracht | 1 |
|
0.135, .. | Hadronen | |
| Sterke | 1 | Confinement | 8 Gluonen | 0 | Quarks |
Tabel 4 laat zien dat de natuur is opgebouwd uit
fermionen: quarks en leptonen; deeltjes met halftallige
spin (![]() ), die Fermi-Dirac statistiek volgen.
De onderlinge wisselwerkingen van
deze fermionen worden overgebracht door uitwisseling van andere deeltjes.
Deze uitgewisselde deeltjes zijn bosonen, hebben heeltallige
spin (0, 1, 2) en gedragen zich daarom volgens de Bose-Einstein statistiek.
), die Fermi-Dirac statistiek volgen.
De onderlinge wisselwerkingen van
deze fermionen worden overgebracht door uitwisseling van andere deeltjes.
Deze uitgewisselde deeltjes zijn bosonen, hebben heeltallige
spin (0, 1, 2) en gedragen zich daarom volgens de Bose-Einstein statistiek.
Merk op dat neutrinos slechts voor één enkele wisselwerking gevoelig zijn, namelijk de zwakke wisselwerking, indien we aannemen dat hun massa nul is. Leptonen zijn niet gevoelig voor de sterke wisselwerking, zodat enkel de quarks alle wisselwerkingen ondergaan.
In tabel 4 is de karakteristieke sterkte van de
wisselwerking aangegeven met een dimensieloos getal. We zullen deze
procedure toelichten aan de hand van de elektrostatische potentiaal.
De potentiële energie van twee elementaire ladingen, die zich op een
afstand ![]() van elkaar bevinden, bedraagt
van elkaar bevinden, bedraagt
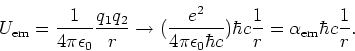 |
(8) |
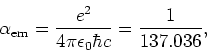 |
(9) |
Analoog vinden we voor de gravitatie van twee protonen de energie
| (10) |
| (11) |
Voor zowel de zwakke wisselwerking,
![]() , als
de sterke wisselwerking,
, als
de sterke wisselwerking,
![]() , zijn in de literatuur
ook andere normeringen gebruikelijk.
, zijn in de literatuur
ook andere normeringen gebruikelijk.
Men kan de elektromagnetische krachten, die tussen twee ladingen werken,
beschrijven in QED met behulp van de uitwisseling
van een of meerdere fotonen. Zo wordt bijvoorbeeld de wisselwerking tussen
een elektron en een positron door de Feynman diagrammen
gegeven in figuur 1 beschreven.
In dit college nemen we aan dat in de Feynman diagrammen de tijdas
horizontaal is (de toekomst is rechts). In de literatuur vindt men ook
andere conventies.
De fotonen
geschetst in figuur 1 zijn virtuele deeltjes (en
zijn bijvoorbeeld niet massaloos).
De uitwisseling van een massaloos foton komt overeen met de
Coulombpotentiaal met een oneindige dracht.
Grofweg zouden we
ons de deeltjesuitwisseling als volgt kunnen voorstellen: als twee
ladingen ![]() en
en ![]() zich op een afstand
zich op een afstand ![]() van
elkaar bevinden, dan kunnen er volgens de onzekerheidsrelatie
fotonen met een impulsoverdracht
van
elkaar bevinden, dan kunnen er volgens de onzekerheidsrelatie
fotonen met een impulsoverdracht
| (12) |
| (13) |
| (14) |
Door het uitvoeren van
nucleon-nucleon verstrooiingsexperimenten
heeft men vastgesteld dat de kernkracht een eindige dracht
heeft (
![]() fm).
In de eenvoudigste benadering
(en met verwaarlozing van alle spineffecten) kan de
kernkracht gevonden worden uit
fm).
In de eenvoudigste benadering
(en met verwaarlozing van alle spineffecten) kan de
kernkracht gevonden worden uit
| (15) |
De Japanse fysicus Hideki
Yukawa heeft reeds in 1935 de suggestie gedaan, dat deze
kracht overgebracht kan worden door uitwisseling van deeltjes
met een rustenergie van
| (16) |
Daadwerkelijk werden deze deeltjes dan ook14 in 1947 door Cecil Powell,
hij werkte in laboratoria in het hoogggebergte (o.a. in
de Andes op 5000 m hoogte), via sporen
in fotografische emulsies gebruikt in
kosmische stralingsexperimenten aangetoond.
Het gaat hier om de drie pionen, ![]() en
en ![]() . De
neutron-proton wisselwerking kan dan (in laagste orde!) door de
diagrammen in figuur 2 beschreven worden.
. De
neutron-proton wisselwerking kan dan (in laagste orde!) door de
diagrammen in figuur 2 beschreven worden.
Een exacte afleiding van het verband tussen de vorm van de
Yukawa potentiaal en de massa van het uitgewisselde deeltje kan
pas later gegeven worden. We beperken ons hier tot een heuristisch
argument:
Indien een uitwisselingsdeeltje met een van nul verschillende
massa door een nucleon geëmitteerd wordt, bijvoorbeeld ![]() , dan gaat
dit altijd gepaard met het schenden
van de wet van behoud van energie.
Deze energie,
, dan gaat
dit altijd gepaard met het schenden
van de wet van behoud van energie.
Deze energie, ![]() , mag door het nucleon `geleend' worden,
mits het wordt `terugbetaald' binnen een tijd
, mag door het nucleon `geleend' worden,
mits het wordt `terugbetaald' binnen een tijd ![]() 15.
De onzekerheidsrelatie
`laat zulks toe' voor een beperkte tijdsduur
15.
De onzekerheidsrelatie
`laat zulks toe' voor een beperkte tijdsduur ![]() , waarbij
, waarbij
| (17) |
| (18) |
We zijn er nu aan gewend dat de krachtwetten voor
gravitatie16 en
de elektromagnetische wisselwerking er zeer eenvoudig uitzien.
Dit is echter geenszins het geval voor de kernkracht. Integendeel,
deze krachtwet is zeer gecompliceerd. We zullen
er enkele aspecten uitlichten.
![]() de radiële afhankelijkheid is ingewikkeld en kan
in de meest eenvoudige benadering beschreven worden door een
superpositie van verschillende Yukawa potentialen.
De reden van de ingewikkelde radiële afhankelijkheid
is het feit dat er verschillende mesonen bestaan, die elk een
bijdrage tot de nucleon-nucleon wisselwerking geven.
de radiële afhankelijkheid is ingewikkeld en kan
in de meest eenvoudige benadering beschreven worden door een
superpositie van verschillende Yukawa potentialen.
De reden van de ingewikkelde radiële afhankelijkheid
is het feit dat er verschillende mesonen bestaan, die elk een
bijdrage tot de nucleon-nucleon wisselwerking geven.
![]() Naast de diagrammen gegeven in figuur 2
zijn er oneindig veel andere diagrammen, die in een
exacte berekening allemaal meegenomen dienen te worden.
In QED convergeert de bijbehorende
reeks, omdat de koppelingsconstante (
Naast de diagrammen gegeven in figuur 2
zijn er oneindig veel andere diagrammen, die in een
exacte berekening allemaal meegenomen dienen te worden.
In QED convergeert de bijbehorende
reeks, omdat de koppelingsconstante (
![]() )
klein is. Dat is echter niet het geval in de kernfysica
(
)
klein is. Dat is echter niet het geval in de kernfysica
(
![]() )
)
![]() De interactiepotentiaal is niet centraal,
maar bevat diverse componenten die van de spin afhangen. Van
belang zijn de spin-spin koppeling, de spin-baan koppeling en
de tensor interactie.
De interactiepotentiaal is niet centraal,
maar bevat diverse componenten die van de spin afhangen. Van
belang zijn de spin-spin koppeling, de spin-baan koppeling en
de tensor interactie.
![]() De interactie is bijzonder slecht bekend
voor kleine afstanden tussen de nucleonen (
De interactie is bijzonder slecht bekend
voor kleine afstanden tussen de nucleonen (![]() fm). Vermoedelijk
dienen ook niet-locale componenten in rekening gebracht te
worden17.
fm). Vermoedelijk
dienen ook niet-locale componenten in rekening gebracht te
worden17.
![]() Er zijn aanwijzingen voor het
bestaan van meer-deeltjes krachten. Dit
betekent dat de wisselwerking tussen twee nucleonen verandert,
als er nog een derde (of meer)
hadron in het interactiegebied gebracht wordt.
De grootte van deze meer-deeltjes kracht is nog onbekend
en wordt daarom op dit moment
in veel experimenten met drie-nucleon systemen onderzocht.
Er zijn aanwijzingen voor het
bestaan van meer-deeltjes krachten. Dit
betekent dat de wisselwerking tussen twee nucleonen verandert,
als er nog een derde (of meer)
hadron in het interactiegebied gebracht wordt.
De grootte van deze meer-deeltjes kracht is nog onbekend
en wordt daarom op dit moment
in veel experimenten met drie-nucleon systemen onderzocht.
We verbazen ons tegenwoordig niet meer over deze gecompliceerde vorm van de nucleon-nucleon interactie. We weten immers dat de nucleonen en mesonen zelf een inwendige structuur hebben en uit meerdere deeltjes (de quarks, antiquarks en gluonen) zijn samengesteld.
De kernkracht is terug te voeren tot de onderliggende sterke
wisselwerking, die de quarks (en antiquarks) door
middel van gluonen
samenbindt. De potentiaal tussen een quark en een antiquark, die
samen een meson vormen, bevat twee termen,
| (19) |
Veel fysici hebben, ondanks tientallen jaren van frustratie, de hoop
niet opgegeven, dat alle vier de wisselwerkingen zich uiteindelijk
zullen laten verenigen in één enkele theorie. Als dat
lukt leidt dat tot unificatie van alle interacties, waarbij
alle krachten manifestaties zijn van verschillende aspecten van
slechts één enkele interactie. Tot nu toe is dat wel
gelukt met de zwakke en de elektromagnetische wisselwerking.
Het zogenaamde standaard model van de elektrozwakke
interactie van Glashow, Salam en
Weinberg (1961) laat bijvoorbeeld toe het ![]() -verval
van deeltjes en kernen te begrijpen en met goede nauwkeurigheid
te berekenen (zie figuur 3).
-verval
van deeltjes en kernen te begrijpen en met goede nauwkeurigheid
te berekenen (zie figuur 3).
Hetzelfde model beschrijft ook de zogenaamde neutrale stromen en de creatie van de intermediare vector bosonen van de zwakke wisselwerking bij elektron-positron botsers. De laagste-orde diagrammen voor dit proces worden gegeven in figuur 112.
Tenslotte, merken we nog op dat de gravitatiekracht dermate zwak is
(
![]() ), dat ze in de kern-
en deeltjesfysica tot nu toe geen rol schijnt te spelen. We zullen
haar dan ook in het vervolg verwaarlozen. Het uitwisselingsdeeltje
is het nog niet experimenteel aangetoonde graviton, een
deeltje met spin 2.
), dat ze in de kern-
en deeltjesfysica tot nu toe geen rol schijnt te spelen. We zullen
haar dan ook in het vervolg verwaarlozen. Het uitwisselingsdeeltje
is het nog niet experimenteel aangetoonde graviton, een
deeltje met spin 2.