Elektron-Nucleon Verstrooiing

Uit energie- en impulsbehoud voor een elastische verstrooiing van een elektron aan een nucleon (massa ) krijgen we, indien de terugstootimpuls , die overgedragen wordt op het nucleon, voldoende klein is, , en als we voor het nucleon de niet-relativistische kinematische betrekking mogen gebruiken

(110)

In de hoge-energie fysica is het gebruikelijk om de werkzame doorsnede als functie van (in plaats van ) uit te drukken. We vinden dan

(111)

Hiermee vinden we voor de werkzame doorsnede de eenvoudige relatie

(112)

We benadrukken nogmaals, dat de verstrooiing in een puur Coulombveld, , overeenkomt met de factor . Tot nu toe hebben we de spin en de magnetische momenten van alle deeltjes verwaarloosd. In het volgende dienen we nog de noodzakelijke correcties aan te brengen. In principe moeten we, tenminste voor het elektron, een relativistisch correcte beschrijving gebruiken. Echter omdat we in dit inleidend college bewust afzien van het gebruik van de Diracvergelijking, moeten we proberen, met een aantal meer of minder goed beargumenteerde aannamen het correcte resultaat te raden⁵². Een elektron dat zich met hoge snelheid in het elektrische veld van een lading beweegt, `voelt' (in het rustsysteem) ook een magnetisch veld . Dit magnetisch veld zal wisselwerken met het magnetisch moment van het elektron. De grootte van deze correctie werd door Mott afgeleid

(113)

In de limiet krijgen we weer de Rutherford werkzame doorsnede. Voor ultra-relativistische elektronen, , worden de effecten van de magnetische velden aanzienlijk

(114)

vooral voor grote verstrooiingshoeken, .

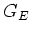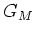Figure: Elektron-proton verstrooiing met 188 MeV elektronen (R.W. McAllister en R. Hofstadter, Phys. Rev. 102, 851 (1956)). De theoretische curves corresponderen met de volgende waarde voor $G_E$ en $G_M$: Mott (1,0), Dirac (1,1), anomaal (1, 2.79).

Indien we ook het magnetisch moment van het nucleon in beschouwing nemen, dan treden er in plaats van twee vormfactoren op: bevat de invloed van de ladingsverdeling, terwijl die van de magnetische momenten bevat. We vinden hiermee de Rosenbluth vergelijking

(115)

waarbij .

Fig. 56 toont data verkregen met de verstrooiing van 188 MeV elektronen aan waterstof. De vergelijking van de diverse theoretische uitdrukkingen voor de werkzame doorsnede met de data leert dat het proton geen puntvormig deeltje is. Deze energie is echter te klein om de vormfactoren over een groot gebied te bepalen. Hogere energieën zijn vereist voor een beter begrip van de structuur van het proton.

De individuele vormfactoren kunnen experimenteel verkregen worden door de werkzame doorsnede voor een bepaalde waarde van te delen door en te plotten als functie van , zoals getoond wordt in Fig. 57. Deze procedure wordt de Rosenbluth separatie genoemd.

Figure 57: Een Rosenbluth plot voor elektron-proton verstrooiing bij een vaste waarde van de overgedragen impuls, 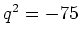$q^2 =-75$ fm$^{-2}$.

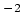Meetgegevens voor de magnetische vormfactor worden getoond in fig. 58. De vormfactor representeert de Fouriergetransformeerde van de verdeling van magnetisme in het proton. Op analoge wijze vertegenwoordigt de verdelingsfunctie van de lading. Uit de data voor verstrooiing van elektronen aan het proton en neutron volgt een schalingswet voor de vormfactoren⁵³

(116)

en men kan eenvoudig nagaan dat uit de afhankelijkheid van vormfactoren volgt dat fm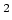$^2$. De nucleonen zijn dus geen puntvormige `elementaire deeltjes'.

Figure 58: Magnetische vormfactor 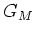$G_M$ van het proton, genormeerd door delen met het magnetisch moment van het proton, als functie van het kwadraat van de overgedragen impuls. De getrokken curve toont een empirische dipool fit aan de data.

De vormfactoren van het neutron worden bepaald uit verschilmetingen voor verstrooiing aan waterstof- en deuteriumtargets. Tot nu toe is het niet gelukt om de elektrische vormfactor van het neutron, , die klein (de totale lading is nul) maar niet nul (het neutron is uit geladen quarks samengesteld) is, met voldoende nauwkeurigheid te bepalen. Wel zijn er nauwkeurige meetgegevens voor . We kunnen schrijven

(117)

De eerste term (Foldy term) geeft de bijdrage van de interactie van het magnetisch moment van het neutron met het Coulomb veld van het elektron. De bijdrage van de Foldy term bedraagt

(118)

De bijdrage van een eventuele elektrische lading `binnen' het neutron geeft aanleiding tot de gemiddelde kwadratische straal van het neutron en deze bedraagt

(119)

We vinden dus ruwweg dat het neutron alleen magnetisme bevat en slechts heel weinig lading. Deze eigenschap is moeilijk te begrijpen op basis van eenvoudige modellen.

In de nabije toekomst hoopt men de elektrische en magnetische vormfactoren van het neutron met grote precisie te bepalen. Dit kan in de komende jaren gebeuren met gepolariseerde elektronenbundels ( GeV) en gepolariseerde deuterium en/of 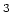$^3$He targets⁵⁴.