Ladingsverdeling uit Elektronenverstrooiing

In de vorige sectie hebben we de verstrooiing van 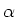$\alpha$-deeltjes aan kernen besproken en zijn we tot de volgende belangrijke conclusies gekomen:

• Uit de goede overeenstemming tussen de klassieke theorie en de resultaten van experimenten blijkt dat de wet van Coulomb
  

  (81)

  
  
  ook voor zeer kleine afstanden ( fm) exact geldig is.
• De totale lading van de kern bevindt zich binnen een bol met straal .
• De sterke wisselwerking, die de nucleonen bindt binnen een kern, heeft een zeer korte dracht ( fm) - anders zouden er afwijkingen van de Coulombwet optreden.
• `Toevallig' levert een quantummechanische berekening (in de eerste-orde Born benadering) een werkzame doorsnede (niet door ons uitgerekend) die gelijk is aan wat we vinden met een klassieke berekening.

Hier zullen we de elastische verstrooiing van elektronen (dus negatief geladen deeltjes) aan kernen bespreken. Elektronen hebben als voordeel, dat ze net als de andere leptonen niet meedoen aan de sterke wisselwerking, en we dus niet een nieuwe, voorlopig onbekende, kracht hoeven in te voeren. Daarentegen willen we nu verstrooiingsexperimenten behandelen, waarbij we nog kleinere afstanden van de wisselwerking ( fm) aftasten en in het bijzonder de ladingsverdeling in het inwendige van de kern willen bepalen. Een verdere vereenvoudiging volgt uit het feit dat we elektronen als puntvormige elementaire deeltjes kunnen beschouwen.

Een eenvoudige schatting laat zien, dat we voor dergelijke experimenten hoogenergetische elektronen () dienen te gebruiken. Om een plaatsresolutie van fm te bereiken, hebben we een elektronenbundel met een voldoend kleine de Broglie golflengte nodig. Uit de optica (het oplossingsvermogen van een microscoop) weten we dat twee punten enkel dan gescheiden kunnen worden, indien

(82)

Hiermee vinden we direct⁴⁹ dat

(83)

(84)

Teneinde de werkzame doorsnede te berekenen gebruiken we weer de gouden regel van Fermi (nu in het laboratoriumsysteem) en de kinematiek zoals gedefinieerd in figuur 50.

Figure 50: Schematische voorstelling van de verstrooiing van een elektron aan een kern. De viervectoren van het inkomende en verstrooide elektron, en de overgedragen vierimpuls zijn gedefinieerd.

Er wordt een energie en een impuls overgedragen aan een kern met massa . Na integratie over de delta functies krijgen we voor de differentiële werkzame doorsnede

(85)

We bespreken eerst het ultra-relativistische geval

(86)

en krijgen

(87)

De correctiefactor, , voor de terugstoot ( recoil factor) van de kern wordt gelijk aan 1 in de limiet .

In de niet-relativistische limiet hebben we

(88)

waarbij de zogenaamde verstrooiingsamplitude is.

Figuur 51 toont dat voor grote afstanden tussen de beide reactiedeeltjes geldt dat

(89)

In het volgende zullen we het matrixelement 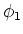$M_{fi}$ uitrekenen in eerste-orde Born benadering⁵⁰.

Figure 51: Schematische voorstelling van de verstrooiing van deeltjes. Verklaring van de verstrooiingsamplitude.

We gebruiken vlakke golven voor en , en krijgen

(90)

waarbij de potentiaal is, die de wisselwerking beschrijft. Indien we sferische symmetrie aannemen, , dan vinden we

(91)

Om te beginnen berekenen we het matrixelement voor een afgeschermde Coulombpotentiaal

(92)

Hiermee houden we rekening met het feit, dat de lading van de targetkern voor grote afstanden door de elektronenwolk afgeschermd wordt. De constante is van de orde van de atoomstraal, dus Å= 10 fm. We vermijden dan ook direct convergentieproblemen (de totale werkzame doorsnede voor de Coulombpotentiaal is oneindig groot!).

Voor de integraal vinden we

(93)

Indien de terugstootimpuls niet al te klein is,

(94)

dan valt de afschermparameter eruit en krijgen we als eindresultaat

(95)

Figure 52: Verstrooiing van een elektron aan een kern met een eindige sferisch symmetrische ladingsverdeling.

In het niet-relativistische grensgeval volgt voor de verstrooiingsamplitude

(96)

en voor de overgedragen impuls

(97)

waarbij in het zwaartepuntsysteem en met

(98)

krijgen we weer de werkzame doorsnede volgens de eenvoudige, vroeger klassiek afgeleide, formule van Rutherford:

(99)

Voor elektronen volgt dan

(100)

Figure 53: Verstrooiing van elektronen met een energie van 153 MeV aan kernen van goudatomen.

Een vergelijking van deze uitdrukking met de resultaten van experimenten laten grote afwijkingen zien. We vragen ons daarom af hoe we ons resultaat dienen te modificeren, indien we niet van een puntlading, maar van een uitgebreide sferisch symmetrische ladingsverdeling uitgaan (zie figuur 52). Er geldt dan dat

(101)

waarbij we de ladingsverdeling op 1 genormeerd hebben. Voor het matrixelement krijgen we

(102)

waarbij de Fourier getransformeerde van de ladingsverdeling is en bekend staat als de vormfactor.

Figure 54: Werkzame doorsnede, vormfactor, en ladingsverdeling voor de verstrooiing van elektronen aan loodkernen.

Omgekeerd kunnen we uit direct de gezochte ladingsverdeling,

(103)

verkrijgen. Het is de moeite waarde om dit resultaat te vergelijken met Fraunhofer diffractie aan een spleet⁵¹.

We kunnen opmaken uit figuur 53 dat we, indien we voor de interpretatie van de data voor de verstrooiing van 153 MeV elektronen aan een goudfolie een ladingsverdeling kiezen die homogeen verdeeld is in een bol met straal fm, al direct een veel betere overeenstemming bereiken dan het geval is voor een puntlading. De oscillaties zijn echter nog te sterk (diffractie aan een spleet met scherpe kanten). Een nagenoeg perfecte overeenstemming met de data wordt verkregen, indien we voor de ladingsverdeling de functie

(104)

met fm fm, voor , en fm kiezen.

Figuur 54 laat data zien voor elektronenverstrooiing aan lood (merk op dat de werkzame doorsnede over het meetgebied veranderd met twaalf ordes van grootte). De figuur toont de werkzame doorsnede, de bijbehorende vormfactor , en de hieruit afgeleide ladingsverdeling. Figuur 55 geeft een overzicht van de ladingsverdeling van een aantal kernen. We zien dat de ladingsdichtheid in het kerninwendige bij alle kernen ongeveer even groot is. Kleine afwijkingen kunnen voor een deel door het schillenmodel verklaard worden.

Figure 55: Ladingsverdelingen voor een aantal kernen, zoals bepaald met behulp van elektronenverstrooiing.

We hebben gezien dat onder bepaalde voorwaarden (verwaarloosbare terugstoot van de kern, Born benadering, spinloze kern) de vormfactor identiek is aan de Fourier getransformeerde van de ladingsverdeling. De ladingstraal van de kern wordt gevonden door de vormfactor te beschouwen voor het geval waar de golflengte significant groter is dan de kernstraal , en dus

(105)

We ontwikkelen naar machten van en vinden

(106)

We definiëren de gemiddelde kwadratische ladingstraal als

(107)

en vinden

(108)

Het is dus nodig om de vormfactoren te meten tot zeer kleine waarden van de overgedragen impuls, indien we de ladingstraal willen bepalen. Er geldt

(109)