


Next: Werkzame Doorsneden en Matrixelementen
Up: HADRON STRUCTUUR
Previous: HADRON STRUCTUUR
De kinematische aspecten van verstrooiingsexperimenten zijn gelijk voor alle
wisselwerkingen. Hier vragen we ons af hoe vaak bepaalde reacties
zullen optreden. Als maat voor de waarschijnlijkheid voeren we
het begrip werkzame doorsnede in. Zoals we later zullen zien, hangt
de werkzame doorsnede af van de sterkte, de dracht, en verdere eigenschappen
van de wisselwerking, alsook van de structuur van de reactiepartners.
De allereerste experimenten werden uitgevoerd met deeltjes afkomstig van
radioactieve bronnen (voornamelijk 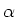 -straling)
en kosmische straling. Tegenwoordig gebruikt men in het
algemeen32 versnellers
om een deeltjesbundel (primaire bundels: protonen, elektronen;
secundaire bundels: pionen, kaonen, zware ionen, enz.) te produceren,
die dan op een vast target ( `fixed-target' experimenten)
gericht wordt. Teneinde
een hoge energie in het zwaartepuntsysteem te verkrijgen, is het
voordelig om botsende deeltjesbundels te gebruiken ( `collider'
experimenten).
-straling)
en kosmische straling. Tegenwoordig gebruikt men in het
algemeen32 versnellers
om een deeltjesbundel (primaire bundels: protonen, elektronen;
secundaire bundels: pionen, kaonen, zware ionen, enz.) te produceren,
die dan op een vast target ( `fixed-target' experimenten)
gericht wordt. Teneinde
een hoge energie in het zwaartepuntsysteem te verkrijgen, is het
voordelig om botsende deeltjesbundels te gebruiken ( `collider'
experimenten).
Figure:
Schematische weergave van de verstrooiing van een deeltjesbundel
aan een trefplaat.
|
Figuur 27 laat zien dat wanneer een bundel een target,
dat 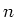 atomen per volumeeenheid (m
atomen per volumeeenheid (m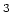 ) bevat, treft, de waarschijnlijkheid
) bevat, treft, de waarschijnlijkheid
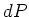 dat een reactie optreedt in de dunne laag
dat een reactie optreedt in de dunne laag 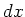 gegeven wordt
door (de bundel bestrijkt een oppervlakte
gegeven wordt
door (de bundel bestrijkt een oppervlakte 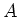 )
)
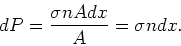 |
(42) |
De door deze vergelijking gedefinieerde grootheid 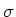 kan
naïef gezien worden als de oppervlakte van het te raken
object voor de desbetreffende reactie33.
Het zal blijken dat deze oppervlakte slechts zelden
gelijk is aan de geometrische
doorsnede van de deelnemende reactiedeeltjes (
kan
naïef gezien worden als de oppervlakte van het te raken
object voor de desbetreffende reactie33.
Het zal blijken dat deze oppervlakte slechts zelden
gelijk is aan de geometrische
doorsnede van de deelnemende reactiedeeltjes (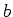 en
en 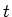 ),
),
en vaak vele ordes van grootte hiervan verschillend is.
Figure:
Totale werkzame doorsnede voor foton verstrooiing aan koolstof
en lood als functie van de energie. De bijdragen van individuele processen
worden getoond, waarbij
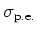 atomair foto-elektrisch
effect (elektron emissie, foton absorptie),
atomair foto-elektrisch
effect (elektron emissie, foton absorptie),
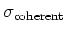 coherente verstrooiing (Rayleigh verstrooiing waarbij het atoom
niet wordt geïoniseerd of aangeslagen),
coherente verstrooiing (Rayleigh verstrooiing waarbij het atoom
niet wordt geïoniseerd of aangeslagen),
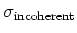 incoherente verstrooiing (Compton verstrooiing aan een elektron),
incoherente verstrooiing (Compton verstrooiing aan een elektron),
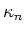 paar-productie in het veld van de kern,
paar-productie in het veld van de kern, 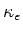 paar-productie in het veld van het elektron,
paar-productie in het veld van het elektron,
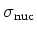 foto-nucleaire absorptie (in het algemeen gevolgd door emissie van
een neutron of een ander deeltje).
foto-nucleaire absorptie (in het algemeen gevolgd door emissie van
een neutron of een ander deeltje).
|
Typische kernreacties hebben een werkzame doorsnede van ongeveer
Dezelfde reactie kan echter, indien men een resonantie aanslaat,
ook zo'n 100,000 keer sneller verlopen (dus
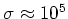 barn).
Omgekeerd hebben reacties, waarbij enkel de zwakke wisselwerking een
rol speelt (bijvoorbeeld
barn).
Omgekeerd hebben reacties, waarbij enkel de zwakke wisselwerking een
rol speelt (bijvoorbeeld
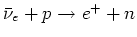 ) werkzame
doorsneden die vele ordes van grootte kleiner zijn (in dit voorbeeld
) werkzame
doorsneden die vele ordes van grootte kleiner zijn (in dit voorbeeld
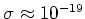 barn).
barn).
Vaak zijn er meerdere reacties gelijktijdig mogelijk. Men definiëert
dan voor elk proces een partiële werkzame doorsnede 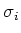 .
De totale werkzame doorsnede,
, is dan de
som34 van alle
partiële werkzame doorsneden
.
De totale werkzame doorsnede,
, is dan de
som34 van alle
partiële werkzame doorsneden
Figuur 28 geeft een overzicht van de totale en
verschillende partiële werkzame doorsneden voor de reacties
en
.
Figure:
Resonanties in de totale werkzame doorsnede voor de verstrooiing
van neutronen aan 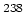 U. De werkzame doorsnede tussen de resonanties
wordt voornamelijk veroorzaakt door elastische verstrooiing.
U. De werkzame doorsnede tussen de resonanties
wordt voornamelijk veroorzaakt door elastische verstrooiing.
|
Heel karakteristiek is de energieafhankelijkheid van de werkzame
doorsnede, indien resonanties optreden. Figuur 29 geeft
de totale werkzame doorsnede voor de verstrooiing van neutronen aan
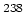 U.
U.
Indien een bundel met intensiteit 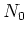 (deeltjes/s) een target treft
met dikte
(deeltjes/s) een target treft
met dikte 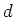 , dan vermindert de intensiteit volgens
, dan vermindert de intensiteit volgens
en er vinden
reacties van het type i plaats35.
Figure:
Schematische voorstelling van de differentiële werkzame doorsnede,
voor processen waarbij de hoekverdeling niet isotroop is.
|
Figuur 30 geeft een schematische voorstelling van de
kinematica voor een
differentiële werkzame doorsnede. De waarschijnlijkheid dat
bijvoorbeeld deeltje 1 uit de reactie
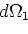 |
(48) |
geëmitteerd wordt in de ruimtehoek 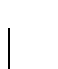 , bedraagt
, bedraagt
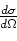 |
(49) |
De differentiële werkzame doorsnede
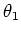 is in
het algemeen niet enkel een functie van de hoek
is in
het algemeen niet enkel een functie van de hoek 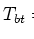 , maar ook
van de energie36en (bijvoorbeeld in het geval van gepolariseerde deeltjes) de
hoek
, maar ook
van de energie36en (bijvoorbeeld in het geval van gepolariseerde deeltjes) de
hoek 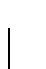 (azimuthale hoek of ook de polarisatierichting).
(azimuthale hoek of ook de polarisatierichting).
Er geldt
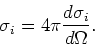 |
(50) |
In het geval dat de werkzame doorsnede isotroop is,
geldt
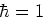 |
(51) |
Op analoge wijze kunnen we ook meer gecompliceerde werkzame
doorsneden definiëren, die soms nodig zijn als er zich meerdere deeltjes
in de eindtoestand bevinden. Deze deeltjes kunnen
in coïncidentie gemeten
worden (dat is meestal het geval in dergelijke experimenten).



Next: Werkzame Doorsneden en Matrixelementen
Up: HADRON STRUCTUUR
Previous: HADRON STRUCTUUR
Jo van den Brand
2002-03-25
![]() -straling)
en kosmische straling. Tegenwoordig gebruikt men in het
algemeen32 versnellers
om een deeltjesbundel (primaire bundels: protonen, elektronen;
secundaire bundels: pionen, kaonen, zware ionen, enz.) te produceren,
die dan op een vast target ( `fixed-target' experimenten)
gericht wordt. Teneinde
een hoge energie in het zwaartepuntsysteem te verkrijgen, is het
voordelig om botsende deeltjesbundels te gebruiken ( `collider'
experimenten).
-straling)
en kosmische straling. Tegenwoordig gebruikt men in het
algemeen32 versnellers
om een deeltjesbundel (primaire bundels: protonen, elektronen;
secundaire bundels: pionen, kaonen, zware ionen, enz.) te produceren,
die dan op een vast target ( `fixed-target' experimenten)
gericht wordt. Teneinde
een hoge energie in het zwaartepuntsysteem te verkrijgen, is het
voordelig om botsende deeltjesbundels te gebruiken ( `collider'
experimenten).
![]() atomen per volumeeenheid (m
atomen per volumeeenheid (m![]() ) bevat, treft, de waarschijnlijkheid
) bevat, treft, de waarschijnlijkheid
![]() dat een reactie optreedt in de dunne laag
dat een reactie optreedt in de dunne laag ![]() gegeven wordt
door (de bundel bestrijkt een oppervlakte
gegeven wordt
door (de bundel bestrijkt een oppervlakte ![]() )
)
![]() .
De totale werkzame doorsnede,
, is dan de
som34 van alle
partiële werkzame doorsneden
.
De totale werkzame doorsnede,
, is dan de
som34 van alle
partiële werkzame doorsneden
![]() U.
U.
![]() (deeltjes/s) een target treft
met dikte
(deeltjes/s) een target treft
met dikte ![]() , dan vermindert de intensiteit volgens
, dan vermindert de intensiteit volgens
 , bedraagt
, bedraagt